大视场反射式施密特光学系统设计与检测

董云芬，王 波，张盈盈，宫 萌，王 斌

（中科院南京天文仪器有限公司，江苏 南京 210000）

引言

天文光学望远镜是观测天体的重要仪器之一，大视场、低成本、高性能天文望远镜是当前研究和开发的热点[1-2]。按照物镜的种类，可将望远镜光学系统分为3 类：折射系统、反射系统、折反系统。大口径、大相对孔径的折射系统需要不同折射率的玻璃搭配成消色差系统，为了消除残余球差，还需引入非球面，且折射系统的透镜材料及加工费用都很高，因此价格也十分昂贵。反射式望远镜在天文望远镜中应用十分广泛[3]，常用的有牛顿系统、卡塞格林系统、格里高利系统等，此类反射系统，对轴外像差校正能力较弱，视场角较小，一般小于±1°，不能满足大视场望远镜的需求[4-5]。折反射望远镜以球面镜为基础，加入适当的折射元件，用来矫正轴外球差，可取得良好的光学质量[6]。

施密特系统具有视场大、像质好等优点，是应用最广泛的折反射系统之一[7]。1931年德国科学家施密特发明了施密特系统，系统由球面反射镜和一块接近平行平板的非球面矫正镜组成，矫正镜位于球面镜球心附近。非球面的面形能够使中央光束略有汇聚，而边缘光束略有发散。矫正板放在球面反射镜的球心，这样能使整个系统的球差得到很好的矫正，且主镜不产生彗差、像散和畸变，仅有场曲[8]。但是，折反式施密特系统不能目视，在科普天文望远镜中甚少使用。我国自主研制的大口径大视场LAMOST 望远镜属于反射式施密特系统，安置于国家天文台兴隆观测站，该系统由4 m 口径的非球面主反射镜和球面镜组成[7]。上海技术物理研究所的雷存栋提出了离轴全反射施密特系统[9]，该系统由离轴非球面主镜和球面镜组成，非球面镜位于球面镜球心，系统筒长较长，离轴非球面也比较难加工，对于低成本的天文望远镜也很少使用。

在现有施密特系统基础上，本文研究了反射式施密特系统的设计方法，推导出斜入射反射式施密特矫正板方程，计算出施密特矫正板初始结构参数，在光路中插入折转反射镜，完成了反射式施密特系统设计。设计的系统缩短了镜筒尺寸，使焦面位于系统外部，具有体积小、加工成本低、成像质量好等优点。

1 施密特矫正板理论计算

首先考虑光束正入射情况。假定平行光束垂直入射施密特校正板，如图1所示。此时施密特校正板方程为

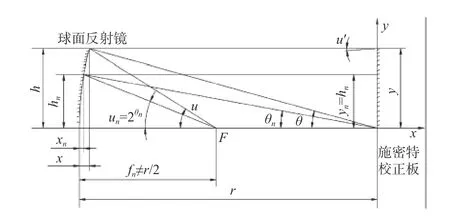
图1 光线垂直入射施密特校正板示意图Fig.1 Schematic diagram of Schmidt correction plate with vertical light incident

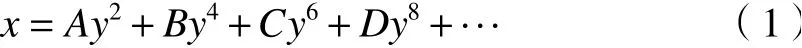
式中：x为施密特矫正板的失高；y为光线高度；A、B、C、D为施密特矫正板特征参数。

我们的主要任务是求出施密特矫正板特征参数，得出施密特矫正板方程。方程级次取多少，要看像差矫正情况，不是越多越好，级次越多检测光路计算也越麻烦[10]。在像差理论基础上求解系数的原则是：首先取定yn带，见图1所示，计算出这个高度的焦点F，再从F 点出发反追迹几条光线，求出经过球面反射镜后的u′角以及在施密特矫正板上的高度y。如果通过校正板后所有的光线都平行于光轴出射，因此校正板上各个高度处的斜率dx/dy和u′有 一定的关系，即 dx/dy=u′/2。

根据非球面方程的特性，系数A与矫正板顶点曲率半径的关系式是R0=1/2A，R0的值使近轴光经过校正板反射和球面镜反射后聚焦到F点，如果R0=∞，则近轴光应聚焦到r/2 处，r是球面反射镜的曲率半径，R0是校正板的顶点曲率半径。

对于取定的yn，有[9]：

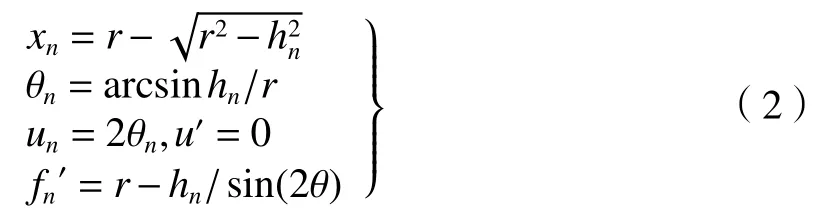
对于任意带，有：

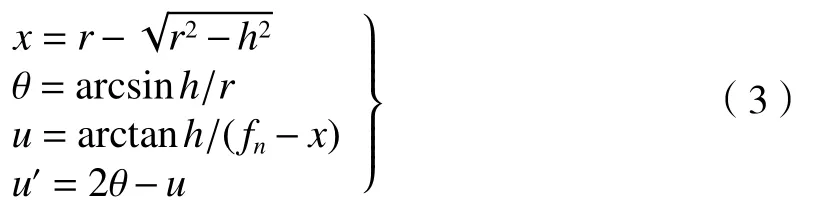
为使近轴区的光汇聚到F点，即离球面镜顶点为fn，可求出二次项系数

若级数取到8 次方为止，（1）式两边对y求倒，则斜率方程可写为

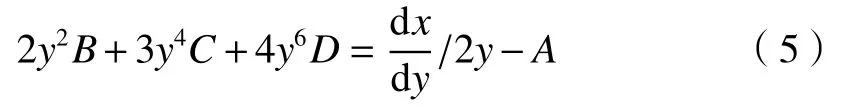
dx/dy=u′/2

当出射光线与光轴平行时，，故有：

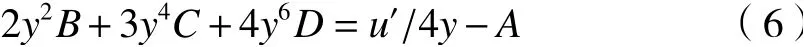
其中

根据（6）式列方程组求解系数B、C、D时，y由（7）式求出。

反射式施密特系统没有色差问题[10]，考虑到方便加工，yn带可选在0.707ymax处，即hn=0.707ymax。实际上正入射的反射式施密特系统没有实际意义，只有将矫正板倾斜一个角度 α，才能使球面镜不会遮挡入射光，α的取值由相对口径决定。

假设施密特矫正板与光轴的倾斜角度是 α，如图2所示。

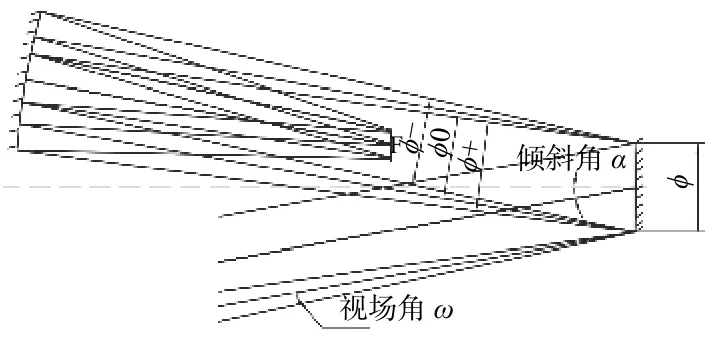
图2 光线斜入射施密特矫正板示意图Fig.2 Schematic diagram of Schmidt correction plate with oblique light incident

由于倾斜的存在需引入弧矢方向坐标z2项，y=y′cosα，y′为倾斜时高度，此时斜入射施密特校正板方程可写为

由（8）式可知，斜放置的施密特矫正板只对零视场光束很好成像，对轴外视场则发生变化，设零视场通光口径为ϕ0，经矫正板反射后的口径为ϕ0=ϕcosα ，而 -ω视场的光束反射后的口径为ϕ-=ϕcos(α+ω)；+ω视场的光束反射后的口径ϕ+=ϕ×cos(α-ω)；由此可得出：ϕ+＞ϕ0，ϕ-＜ϕ0，即投射到球面反射镜上的光束变成椭圆。矫正板对于 ϕ0口径所产生的光线偏斜正好抵消球面镜的球差，对于 ϕ+口 径就成为欠矫正，对于 ϕ-则为过矫正，因此像面有场曲，位于像面的目标接收器需调焦，使轴上和轴外弥散斑相对均匀。

2 大视场反射式施密特系统设计与性能评价

光学系统设计首先要考虑的原则：在外形尺寸、质量以及经费允许的情况下尽可能提高成像质量；综合考虑光学设计指标，光学系统的使用环境，现有的加工、检测、装调条件；另外，在设计过程中要兼顾技术发展现状[11-12]。

本文研究的大视场施密特系统的设计指标如下：系统焦距为f=1 700 mm，视场角 2ω=4◦，有效通光口径400 mm。根据系统焦距f=1 700 mm，设定球面反射镜的曲率半径r=3 400 mm，施密特矫正板顶点曲率半径R0=∞，综合考虑施密特系统的视场角和有效通光口径，选取施密特矫正板倾斜角α =8◦。对于口径400 mm，顶点曲率半径3 400 mm的球面反射镜，由球差公式可求出fn=1 698.03 mm，代入公式（4）中可求出二次项系数A=-1.7×10-7。

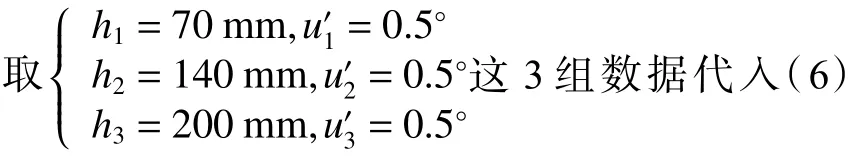
式解方程组可求出，4 次项系数B=5.5×10-12，6 次项系数C=2×10-16，8 次项系数D=-7×10-20。

由（7）式可求出倾斜后的施密特矫正板多项式的各项系数，以正入射的各项系数为初始结构，代入Zemax 中进行优化，为了使结构更加紧凑，加入平面镜折转光路，最终设计参数如表1所示。

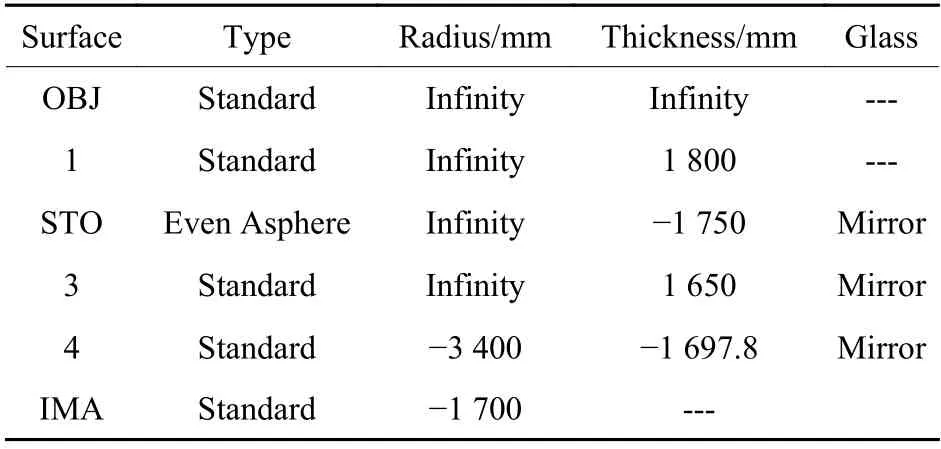
表1 大视场施密特光学系统设计参数Table1 Design parameters of large field Schmidt optical system

矫正板非球面系数中，2 次项系数A=-1.70×10-7，4 次项系数B=3.112×10-12，6次项系数C=4.177×10-19，8 次项系数D=-1.662×10-25。

施密特矫正板方程为

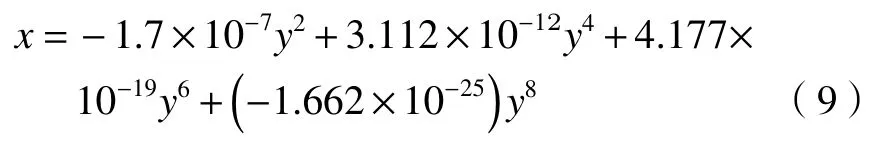
由表1可知，像面位于平面折转镜背部47.8 mm处，像面场曲半径为1 700 mm，置于焦面处的探测器需要倾斜调焦，以使轴上轴外弥散斑相对均匀。光学系统由施密特矫正板、平面折转镜、球面镜组成，反射镜材料均为微晶玻璃，光路结构如图3所示。

图3 系统光路图Fig.3 Optical path diagram of system

光学系统MTF 图如图4所示。从图4可看出设计结果基本接近衍射极限。

图4 MTF 图Fig.4 FFT MTF diagram

光学系统的加工装调误差以及使用环境温度变化均会对成像质量造成一定影响，因此，设计阶段对光学系统做公差分析十分必要。结合现有的加工装调技术，公差分配如表2所示。

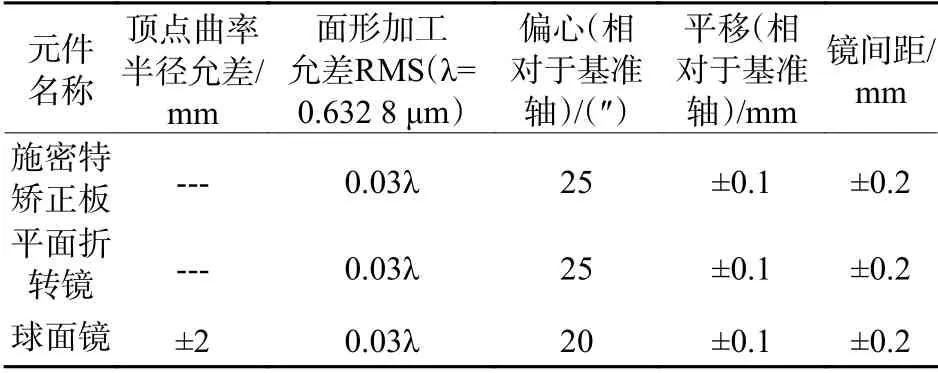
表2 大视场施密特光学系统公差分配Table2 Tolerance data of large field Schmidt optical system

把上述公差代入Zemax 软件，以MTF 作为评价标准，利用灵敏度分析模型进行分析，经分析误差叠加后的MTF 为0.402（100 lp/mm 处），满足一般成像系统的像质要求。对于该系统，环境温度变化主要通过影响镜间距影响成像质量，3 个反射镜之间的支撑结构采用碳纤维，碳纤维的热膨胀系数为0.3×10-6/k，在-20 ℃～30 ℃温度范围内镜间距变化量为±0.2 mm，采用碳纤维做支撑结构能满足系统的公差要求。

3 反射式施密特矫正板的加工及检测

反射式施密特矫正板属于高次非球面，面形精度要求较高，加工制造过程需经过多个“加工-检测-加工”循环完成[13]。在非球面的高精度制造过程中，高精度检测手段为加工过程提供准确的面形误差分布，指导加工，为获得高精度的面形提供保障[14]。

加工施密特矫正板的第1 步是：找出合理的起始球面，并用磨盘磨至起始球面；第2 步：根据三坐标测量的面形数据，通过计算机控制小磨头，按照确定的加工轨迹对非球面光学表面进行研磨或抛光，通过控制磨头在工件表面的驻留时间、磨头与工件间的相对压力以及磨头的转速来控制材料的去除量[15]；第3 步：建立补偿器检测光路，激光测距仪控制检测光路各元件之间的间距，干涉仪测量面形，通过检测与加工过程的反复迭代，实现非球面面形误差逐渐收敛修正，直到满足要求。

高次非球面的检验一直是光学加工中的一个难题，稳定高效的非球面检测手段是光学加工的关键环节[13]。常用的高次非球面反射镜检测方法是零位补偿法检测，补偿元件可以是透镜或者计算全息，在实际应用过程中，绝对零位条件是不存在的，如果检测光路的残余像差对检测结果精度的影响可以忽略不计，那么非零位检测就可以等效成零位检测。本文的施密特矫正板最大修磨量仅为0.005 mm，通过特殊定制的球面透镜结合干涉仪即可完成该非球面的检测，检测原理图如图5所示，检测光路的残余像差如图6所示，残留波像差RMS 为0.000 2 μm，残留像差很小，可以等效为零位检测。

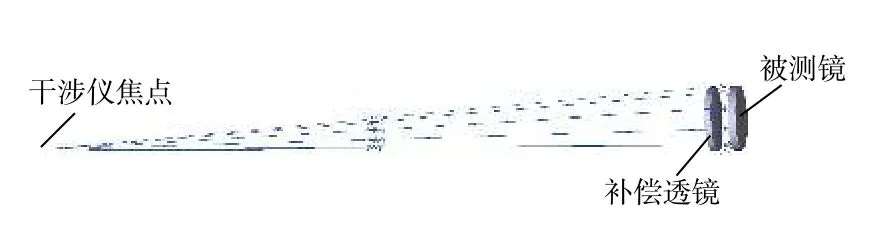
图5 施密特矫正板检测原理图Fig.5 Schematic diagram of Schmidt correction plate detection

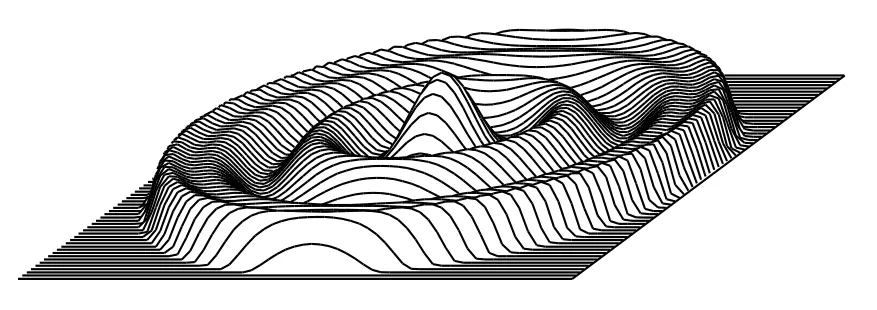
图6 残余波前误差Fig.6 Residual wavefront error

4 结论

基于像差平衡原理由正入射施密特矫正板方程推导出斜入射施密特矫正板方程，提出了大视场反射式施密特系统设计方法，针对焦距1 700 mm，F 数为4.25，波段为0.3 μm～0.9 μm，成像视场角4°的光学系统需求，完成了反射式施密特光学系统设计，该系统在奈奎斯特频率处的调制传递函数MTF 大于0.35，畸变小于2.5%，成像质量达到了衍射极限，经过公差分析，系统满足成像要求。

设计过程中兼顾了技术可实现性及技术发展的先进性，优化设计后施密特校正板与最近球面偏差为0.005 mm，采用定制的补偿器结合干涉仪可完成面形高精度检测，避免了高次非球面检测的难题，能够有效指导施密特矫正板的加工过程。反射式施密特系统成像波段宽，克服了透射式光学系统在大视场下的多波段像差矫正带来的色差问题，光学元件加工成本低且成像质量高，因而具有其他光学系统无法取代的优势。

由于斜置的施密特矫正板只对零视场光束很好成像，对于轴外视场则有一定的像面弯曲，因此反射式施密特系统对于场曲畸变要求较高的系统有局限，需进一步研究。