卡尔曼滤波在光纤测温隧道火灾监测系统中的应用

张 涛 刘 俊 高 媛 罗仕刚

(湖北省交通运输厅鄂西高速公路管理处 武汉 430056)

公路隧道环境相对于普通的公路环境具有很大特殊性，可概括为：空间狭长且密闭、活动范围小、通风差，因此，如果火灾事故发生在隧道内且没有得到及时处理，将产生极大危害。如何充分发挥隧道内火灾报警系统的作用，以实现防患于未然、尽早发现、尽早扑救的目的，是必须重点研究的问题[1]。

由于公路隧道结构的特殊性，当火灾发生在隧道中时，不同于普通较为开阔的公路环境，隧道内的环境温度和烟气浓度(体积浓度)都会在极短时间内达到危险值。隧道发生火灾时，其由于空间狭小密闭，必然导致升温速度很快，一般成灾时间为4～10 min[2]，并且长时间持续高温，在火区中的烟气温度可达到1 000 ℃；隧道火灾发生时，还会产生大量高质量浓度的烟雾，在密闭环境中无法及时扩散排出，大幅度降低隧道内的能见度，增加救援的困难性和危险性。

光纤测温技术以温度作为主要的监测量，可以避开视频分析技术的主要难点：光照干扰和烟雾遮蔽，并且以光缆为传感介质，在监测现场无需供电，不会引入额外的风险，所以非常适合隧道环境的温度和火灾监测。光纤测温火灾监测系统通过布设于高速公路隧道沿线的测温光缆进行连续空间和连续时间的温度采集，实时监测隧道内的各个区域的温度变化，对温度变化发生异常的区域进行预警[3]。比如，当隧道内的某一区域在一定时间内的升温速度过快、变化范围过大时，系统需要发出预警信息，或者隧道内某一区域的测量温度过高时，系统同样需要发出预警信息，因此，系统测温数据的实时性和准确性直接决定了温度监测火灾预警系统的监测效果。为了进一步提高监测系统的可靠性，需要对采集的测温数据进行更为合理有效的预处理，抑制和过滤系统噪声的干扰影响，提高监测系统的灵敏度和有效性，为隧道防灾救灾争取时间。

1 光纤测温数据处理

在现有的滤波降噪方法中，一般采用时域平均、小波分解等方法来抑制噪声[4]；但是这些方法所面临的主要问题是系统计算资源消耗大、信号处理速度较慢，计算所需消耗的时间较长，这些问题限制了测温系统的温度分辨率和测量周期[5]。

1.1 时域平均

时域平均是将系统在一段时间内采集的信号叠加后进行平均，一般认为信号中的随机干扰信号，属于白噪声，是呈正态分布的，均值为0，因此，通过采样信号的叠加，就可以消除信号中的随机干扰，叠加的次数越多，降噪的效果越明显[6]。

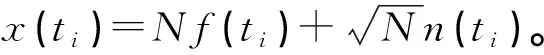
1.2 小波分解

根据温度监测信号的特点，温度的变化一般为相对缓慢的过程，而噪声一般分布于相对较高的频段中，因此，可以通过小波分解的方法，将信号分解到不同的频段中，通过软阈值的方法，计算得到真实信号和噪声干扰各自对应的权重系数，对真实信号的成分进行增强，对噪声干扰的成分进行抑制。小波分解在不同的分解尺度下，将信号分解到不同的频段，在不同的频段中，又将信号分为平均部分和细节部分，再在各个频段中，通过软阈值方法为小波系数分配对应的权重，再将与权重相乘后的小波系数进行重构，即可实现信号将噪[7]。利用小波分解实现降噪，主要可以分为以下3步。

1) 选择1个小波基(如db 5小波基)，确定分解的层次(如分解6层)，通过改变小波分解尺度和反复的卷积计算，对原始信号进行小波分解，得到每一层的高频系数和低频系数，一般认为，低频系数中较多的包含了真实的温度测量信号，而噪声干扰更多的存在于高频系数中。

2) 利用软阈值等方法，在分解得到的每一层的高频系数部分中，计算权重系数，将权重系数与各自对应的高频系数相乘，通过此步骤，对原始信号中的真实信号成分进行增强，对噪声干扰成分进行抑制。

3) 将分解后每一层与权重系数相乘后的高频系数，和各层的低频系数，进行小波重构计算，所得结果即为小波降噪滤波后的信号。

2 卡尔曼滤波应用于测温数据处理

2.1 卡尔曼滤波原理

卡尔曼滤波是一种通过线性系统状态方程，对系统状态进行最优估计的方法，最优估计也可看作是滤波过程[8-9]。卡尔曼滤波主要通过2个互相交替的过程来实现[10]，即可分为：时间更新过程(预测)和测量更新过程(校正)，描述如下。

2.1.1 时间更新过程

时间更新过程又称为预测过程，主要分为以下2个步骤。

1) 进行状态变量的向前推算，定义：第k步的先验状态估计为xk-(此时已知第k步以前的状态情况)，第k步的后验状态估计为xk，控制函数为uk-1，增益矩阵为A，控制输入的增益为B，先验状态的向前推算公式：

xk-=Axk+Buk-1

2) 进行误差协方差的向前推算，定义：先验估计误差的协方差为Pk-，后验估计误差的协方差为Pk-1，增益矩阵为A，过程激励噪声协方差矩阵为Q，误差协方差的向前推算公式为

Pk-=APk-1AT+Q

2.1.2 测量更新过程

又称为校正过程，主要分为以下3个步骤。

1) 进行卡尔曼增益Kk的计算，定义：先验估计误差的协方差为Pk-，增益矩阵为H，噪声协方差矩阵为R，卡尔曼增益计算公式为

Kk=Pk-HT(HPk-HT+R)-1

2) 状态变量为xk，第k步的先验状态估计为xk-，卡尔曼增益Rk，测量变量为zk，增益矩阵为H，由观测变量zk更新估计：

xk=xk-+Kk(zk-Hxk-)

3) 更新误差协方差Pk，卡尔曼增益Kk，增益矩阵H，先验估计误差的协方差Pk-：

Pk=(I-KkH)Pk-

式中：I为单位矩阵。

卡尔曼滤波的计算过程, 其实质上，是一个不断地预测和修正的过程，即是一个最优估计的过程。通过基本方程在时间域内进行递推，因此在最优估计时，不需要大量存储往期数据，在得到新的观测值之后，根据前一时刻的预测状态，测量方差的更新，和卡尔曼因子的更新，就可以计算得到这一时刻的估测值，即得到这一时刻的滤波值，因此，卡尔曼滤波方法具有非常好的实时性，不需要长时间的信号累加过程，能够进行实时计算测量，也不需进行卷积等运算，需要消耗的计算资源少，处理方法简单，易于在硬件中处理和实现，在工程应用中，具有更好的应用价值。

2.2 处理效果比较

选取一段温度探测光缆，放置于常温环境下，在温度探测光缆的前、中、后段随机选取3个探测点，在一段时间内，进行连续的温度数据测量和采集。再对采集的温度探测数据，分别进行时域平均、小波去噪、以及卡尔曼滤波处理，对几种滤波方法的计算效果进行比较。本次实验中，温度探测信号采集时长为10 h，采样率为100 Hz。室温环境在测量开始后的前1.5 h中，开启空调，此时的室温环境在15 ℃左右，之后关闭空调，其后室温逐渐上升到19 ℃左右，通过采集环境温度缓变的数据，验证滤波算法是否能够有效描述温度的变化过程，进行有效的温度测量。

2.2.1 累加时域平均方法

对3个探测点的测温信号，分别进行1 000次(即每段对应10 s数据)和6 000次(即每段对应60 s数据)累加平均处理，1 000次累加时域平均效果见图1(图中白色部分为累加平均值，下同)，6 000次累加时域平均效果见图2。

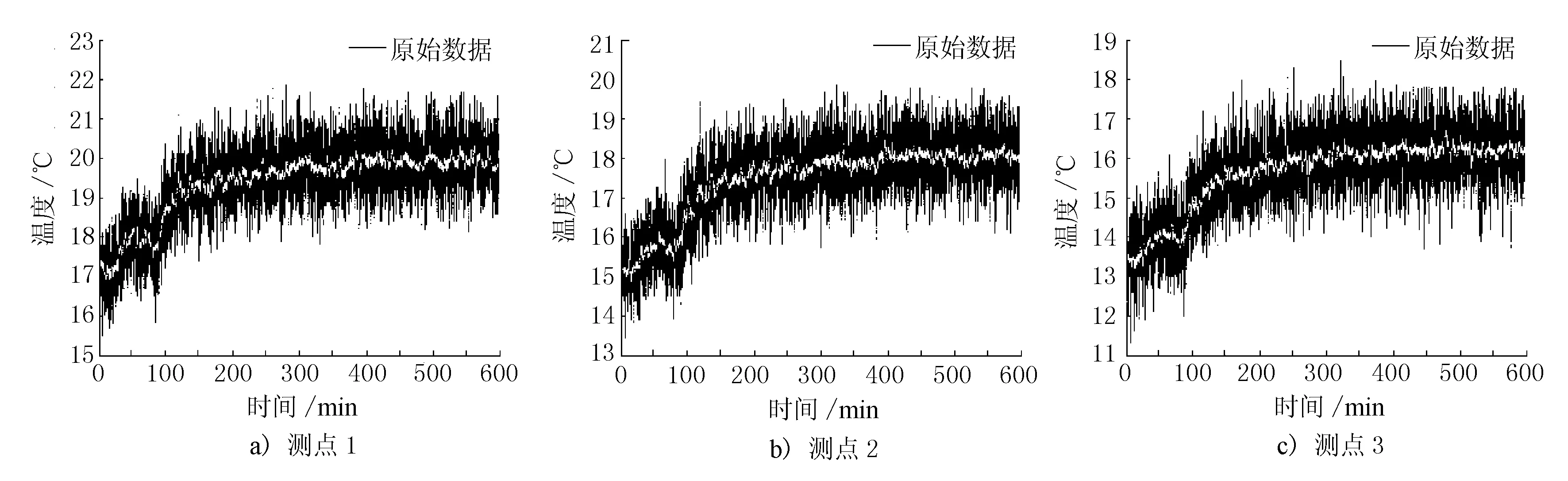
图1 1 000次累加时域平均效果

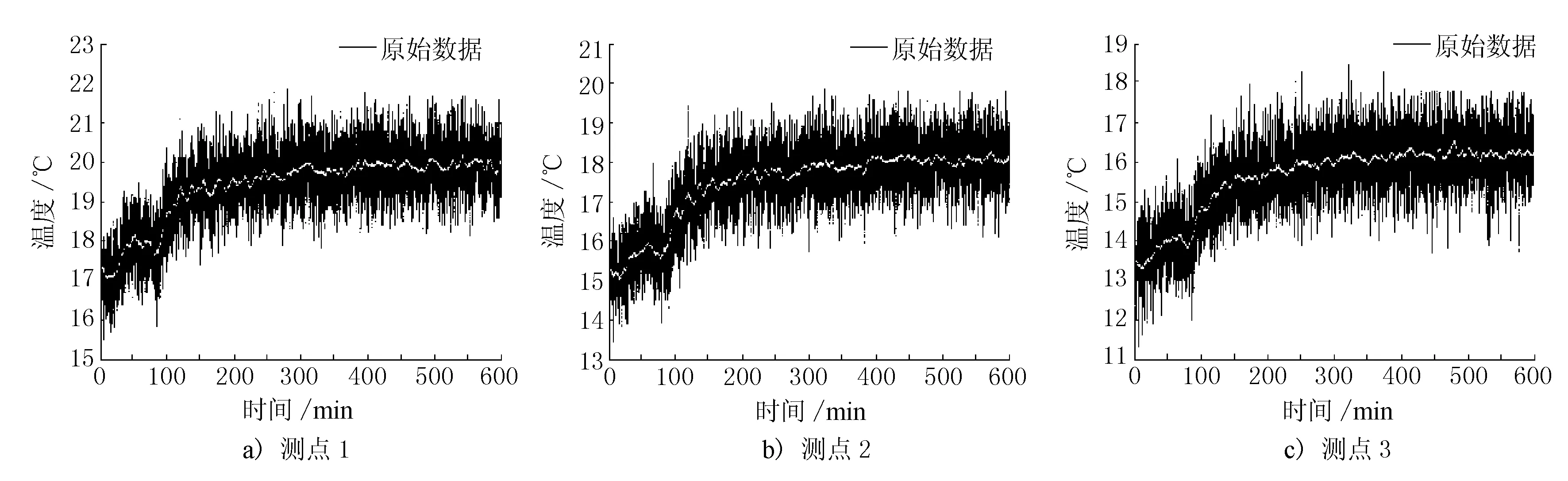
图2 6 000次累加时域平均效果

以上实验结果表明，在测量开始后的前1.5 h中开启空调，经过时域平均滤波后的测温数值在15 ℃左右，之后关闭空调，经过时域平均滤波后的测温数值逐渐上升到19 ℃左右，时域平均滤波算法可以有效描述环境温度的变化。平均累加的方法对测温系统的噪声具有一定的抑制作用，并且，累加的次数越多，采样的时间越长，对噪声的抑制效果越明显，原始温度探测信号的噪声抖动范围约在±3.2 ℃，在累加次数达到1 000次时，温度探测信号的噪声抖动范围可减小到约±1.5 ℃以内；在累加次数达到6 000次时，温度探测信号的噪声抖动范围可减小到约±0.5 ℃以内，但需要的计算时间也越长。

2.2.2 小波去噪方法

选择“db 5”小波，进行6层分解，再利用软阈值方法计算权重系数，进行信号重建，小波去噪处理效果见图3。

图3 小波去噪处理效果

由以上实验结果可得，小波滤波也可以提取测温信号的变化趋势，并且具有一定的抑制噪声抖动的作用。在测量开始后的前1.5 h中开启空调，经过小波去噪滤波后的测温数值在15 ℃左右，之后关闭空调，经过小波去噪滤波后的测温数值逐渐上升到19 ℃左右，小波去噪滤波算法可以有效描述环境温度的变化。经过小波去噪处理后，温度探测信号的噪声抖动范围可减小到约±1.5 ℃以内，但是小波分解所需消耗的计算量也较大，需要进行大量的卷积运算，用来实现一维信号在各个分解尺度上的系数获取。

2.2.3 卡尔曼滤波方法

对信号进行卡尔曼滤波，根据原始信号的噪声抖动范围±3.2 ℃，得到R的取值为10.24，带入卡尔曼滤波计算过程，卡尔曼滤波处理效果见图4。

图4 卡尔曼滤波处理效果

由以上实验结果可得，在测量开始后的前1.5 h中开启空调，经过卡尔曼滤波后的测温数值在15 ℃左右，之后关闭空调，经过卡尔曼滤波后的测温数值逐渐上升到19 ℃左右，卡尔曼滤波算法可以有效描述环境温度的变化。卡尔曼滤波可以有效提取信号的变化趋势，抑制噪声抖动，经过卡尔曼滤波处理后，温度探测信号的噪声抖动范围可减小到约±0.7 ℃以内。

根据以上的实验结果，在第1.5 h关闭空调的时刻前后，卡尔曼滤波算法和时域平均算法、小波去噪算法，都能够准确有效地描述环境温度的变化。并且，卡尔曼滤波算法相对于时域平均算法及小波去噪算法的计算方式，消耗的计算代价更少，具有更好的实时性，易于在计算机硬件上实现，同时能够取得相近甚至更好的滤波降噪效果。

2.3 应用效果对比

在某安装应用现场，使用热风枪对同一段测温光缆进行加热，设定报警温度为70 ℃，测温数据同时接入3个数据处理系统，这3个数据处理系统分别采用累加时域平均方法、小波去噪方法和卡尔曼滤波方法进行测温数据的预处理，记录每个测温系统从开始加热到发出高温报警所用时间，升温实验共进行10次，统计结果见表1。由升温实验高温报警所用时间统计结果比较可得，采用卡尔曼滤波方法进行测温数据预处理的系统，在保证准确有效测量环境温度的同时，具有更好的实时性和灵敏度，卡尔曼滤波方法有效提高了系统测温的稳定性和准确度。

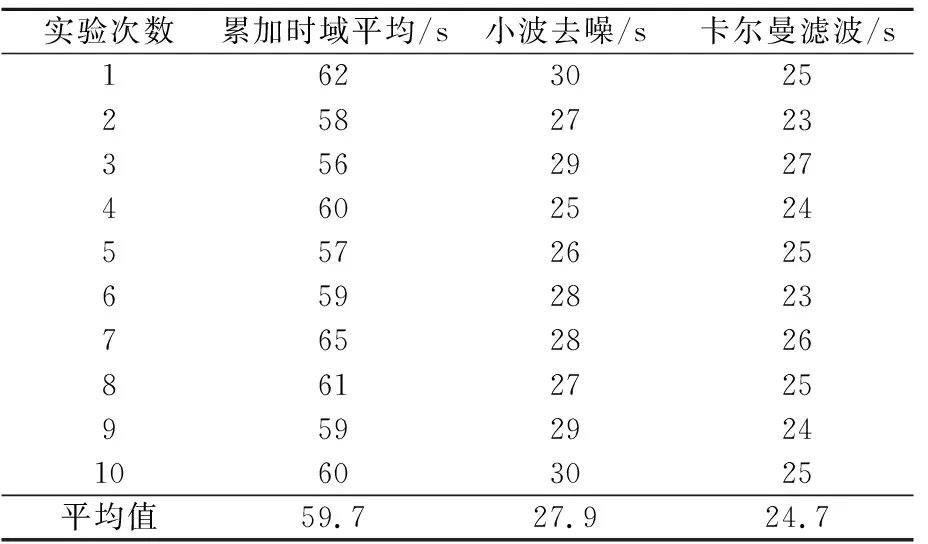
表1 升温实验统计结果

3 结语

将卡尔曼滤波应用于光纤测温隧道火灾监测系统，对测温数据进行滤波降噪处理，经过与现有的时域平均方法和小波去噪方法进行比较，在保证具有相同的温度测量有效性，准确描述温度变化过程的同时，采用卡尔曼滤波可以消耗更少的计算资源和计算时间，具有更好的实时性，并且有效地抑制了系统的噪声干扰，测温数据具有更高的测量精度。在某公路隧道中，经过多次模拟测试和长期运行观察，光纤测温隧道火灾监测系统采用卡尔曼滤波对测温数据进行预处理后，温度监测效果具有更高的报警灵敏度和更低的误报率，监测结果能够对高速公路隧道沿线各个区域的温度异常进行及时的反馈和预警。光纤测温隧道火灾监测系统能够为高速公路隧道的管理者提供科学的参考依据，提升高速公路隧道的智能化管理水平，为高速公路隧道的安全运营保驾护航。