基于几何对称性的椭圆拟合算法
全燕鸣,凌 泉
(华南理工大学 机械与汽车工程学院,广州510641)
椭圆孔在零件中广泛存在,在视觉的工业运用领域中,采用椭圆模型去拟合实际的椭圆孔,通过检测椭圆的位置和大小,完成零件椭圆孔尺寸检测及定位,因此椭圆拟合算法在机器视觉和模式识别等领域内有着广泛的应用。
近年来,学者提出了大量的椭圆检测算法,主要可概括为三类:一类是基于Hough 变换的椭圆拟合方法[1-4],另一类是基于几何特征的拟合方法[5-7],第三类是基于最小二乘法的椭圆拟合方法[8-10]。
本文提出了一种将椭圆对称性及二分法相结合的椭圆拟合算法,使用Halcon 作为图像处理算法库。该方法利用椭圆本身的几何对称性,计算出椭圆中心坐标,再结合二分法,通过逐次迭代逼近的方法计算椭圆的长半轴、短半轴及方向角。最终计算出椭圆的准确参数。本文提出的检测算法,于2019年12月已经运用于明门(中国)幼童用品有限公司的金属管视觉检测中。
1 图像边缘检测方法
边缘检测包括像素级别边缘检测和亚像素级别边缘检测,其中亚像素级别边缘检测,在整像素边缘检测的基础上,采用像素插值和灰度曲线拟合等方法提高边缘检测精度。本文采用Canny 算子提取像素级椭圆边缘并基于高斯拟合的亚像素边缘检测法进一步提高椭圆边缘精度。
2 基于几何对称性的椭圆拟合算法
2.1 椭圆数学模型
椭圆方程的求解,需要确定5 个参数,如图1所示,图中:a,b 为椭圆长短半轴长;x0,y0为椭圆中心坐标;θ 为椭圆长半轴与X 轴之间的夹角(本文中统称为方向角)。该椭圆的方程可以表示为式(1):


图1 椭圆参数示意图Fig.1 Schematic diagram of ellipse parameters
2.2 椭圆的几何对称性
由椭圆的数学模型可知,椭圆关于中心点对称,即作任意角度直线平行线与椭圆相切存在两根切线li,li′(本文统称切线对),相应的存在两切点ci,ci′(本文统称切点对),且圆心位于两切点连线的中点处。切点对的距离记为di;当di最大时,切点对的距离就是椭圆的长轴长;同理,当di最小时,切点对的距离就是椭圆的短轴长,并且此时切线与X 轴的夹角αi即为椭圆的方向角θ,如图2所示。
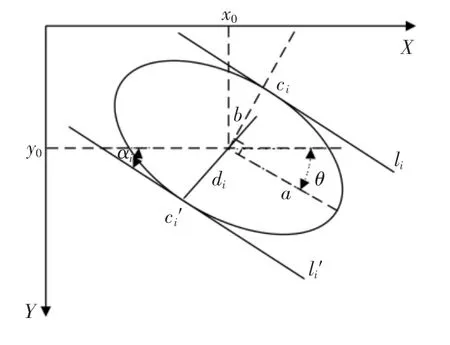
图2 椭圆切线对示意图Fig.2 Schematic diagram of elliptic tangent pairs
2.3 算法原理及流程
1)先对相机进行标定获取内外参,相机采集椭圆孔图像,并进行图像矫正及预处理,采用Canny算子得到椭圆的像素边缘;通过高斯拟合的方法得到椭圆的亚像素边缘[11]。
2) 由2.2 中的椭圆几何对称性计算椭圆中心坐标:计算椭圆不同角度步长(0°~180°之间,角度步长:β=180°/n)的n 组切线对li、li′,可得椭圆切点对坐标:(xi,yi)、(xi′,yi′),以及切点对之间的距离di、切线与X轴的夹角αi,椭圆中心坐标可由式(2)及式(3)计算。

式中:x0、y0为估计的椭圆中心坐标;n 为切点对的对数。
3)通过二分法迭代估计椭圆长半轴长a:通过上一步,可以得到n 个di与αi的值,对n 个di从小到大进行排序,取前2 个记为dk,ds(dk>ds),由此可锁定椭圆长轴长存在于切线角范围为(αk,αs)的角度区域,通过二分法取下一个角度αn+1=(αk+αs)/2,可得到对应新的切线对及切点对的距离:ln+1,l′n+1,dn+1锁定下一个椭圆长轴长出现的切线角区域(αn+1,αn+2),其中:αn+2=(αk+αn+1)/2,如此往复通过二分法在迭代中不断更新逼近椭圆长轴长的真实值,设当迭代到第j 次时,dn+j与dn+j+1差值的绝对值小于设定的迭代阈值ε,此时迭代结束,椭圆长半轴长计算见式(4):

4)同理,计算椭圆短半轴长b 及方向角θ,采用同样的迭代逼近方式,通过2)中获取的数据,对n个di从小到大进行排序,取后2 个记为dv,dp,由此可锁定椭圆短轴长存在于切线角范围为(αv,αp),与3) 中的迭代方式相同,设当迭代到第m 次时,dn+m与dn+m+1的差值绝对值小于设定的迭代阈值ε,此时迭代结束,椭圆的短半轴长及方向角的计算见式(5)及式(6):

通过以上4 步,可以计算出椭圆方程的5 个参数,从而完成椭圆拟合,算法流程详见图3。
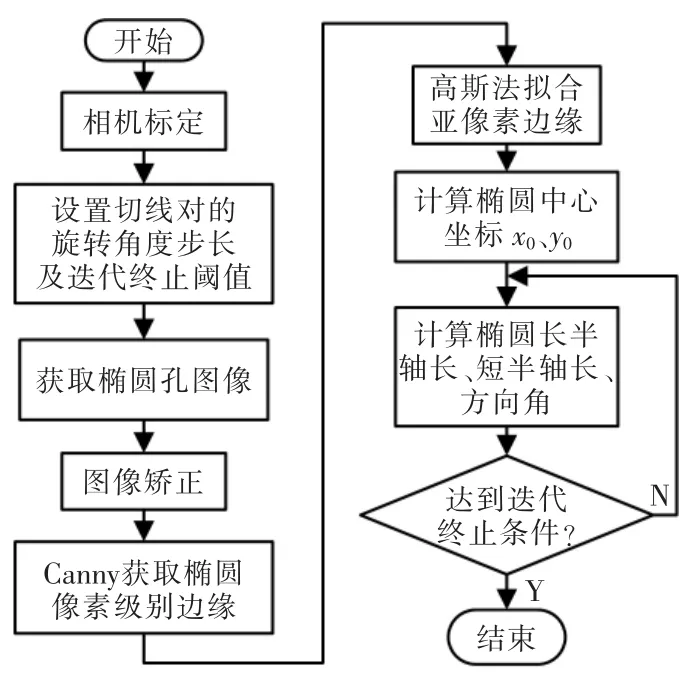
图3 算法流程Fig.3 Algorithm flow chart
3 实验过程
3.1 实验平台及参数配置
本文采用的视觉实验平台如图4,其中包括:视觉检测支架、大恒工业相机(MER-500-7UC),25 mm定焦镜头、球 积分光 源、PC 机(Intel Core i5 处理器,4G 内存,Window10 系统),算法测试软件使用Halcon 开发。

图4 视觉实验平台Fig.4 Visual experiment platform
3.2 实验步骤
1) 通过搭建的视觉实验平台,对相机进行标定:将标定板放在相机的视场内,通过变换标定板的摆放位置、角度获取不同的标定板图像,共采集了18 张不同位置、角度的标定板图像。通过计算18张标定板黑点直径及圆心距离,可计算出相机的内外参,本文采用的标定板见图5。

图5 标定板图Fig.5 Calibration board
2)采集椭圆图像并进行校正:将待测工件的放置于视场中心采集图像,通过上一步中标定出的相机内外参,对图像进行畸变矫正;采集到的零件图见图6、图7。

图6 零件图像Fig.6 Part image

图7 局部椭圆图Fig.7 Partial ellipse
3)获取椭圆亚像素边缘:采用Canny 算子提取椭圆像素级别的边缘;采用文中介绍的基于高斯拟合的亚像素边缘检测法,可提取出椭圆的亚像素边缘,见图8。

图8 椭圆亚像素边缘Fig.8 Elliptical subpixel edge
4)计算切线对与椭圆轮廓的切点对的坐标;取这些切点对连线的中点坐标作为椭圆中心坐标(x0,y0),锁定长半轴、短半轴、方向角出现的角度区域;通过二分法不断迭代逼近,估计椭圆长半轴、短半轴、方向角,当达到迭代停止阈值后(ε=0.1 mm),输出计算结果,椭圆拟合完成。
4 结果与分析
本次实验验证了切线对不同旋转角步长对椭圆拟合精度的影响,实验中采用固定迭代阈值(0.1 mm),分别对比0.5°,1°,1.5°,2°,2.5°,3°,3.5°,4°,4.5°,5°旋转角步长时椭圆的拟合结果,椭圆的实际参数及测量结果见表1。

表1 测量结果与实际值Tab.1 Measurement results and actual values
表1中的数均精确到小数点后三位,由于采用了亚像素边缘提取算法及二分法迭代逼近方法,提高了椭圆拟合的精度,拟合结果可达到实际的零件检测精度要求。表2为切线对在不同旋转角度步长下,得到的椭圆拟合参数与实际值的偏差及对应的算法运行时间。图9为通过表2中的椭圆拟合误差绘制出的误差变化曲线图。

表2 椭圆拟合误差Tab.2 Ellipse fitting error
由图9中的拟合误差曲线可知:椭圆中心坐标的误差,随着旋转角步长β 的增大而增加;椭圆检测算法的运行时间则相反,随着旋转角步长β 的增大而减小;在此次实验中,椭圆中心的最大拟合误差分别为0.074 mm、0.079 mm。算法在实际运用中,用户可以根据实际的测量精度要求选取不同的旋转角度步长,进行调节。
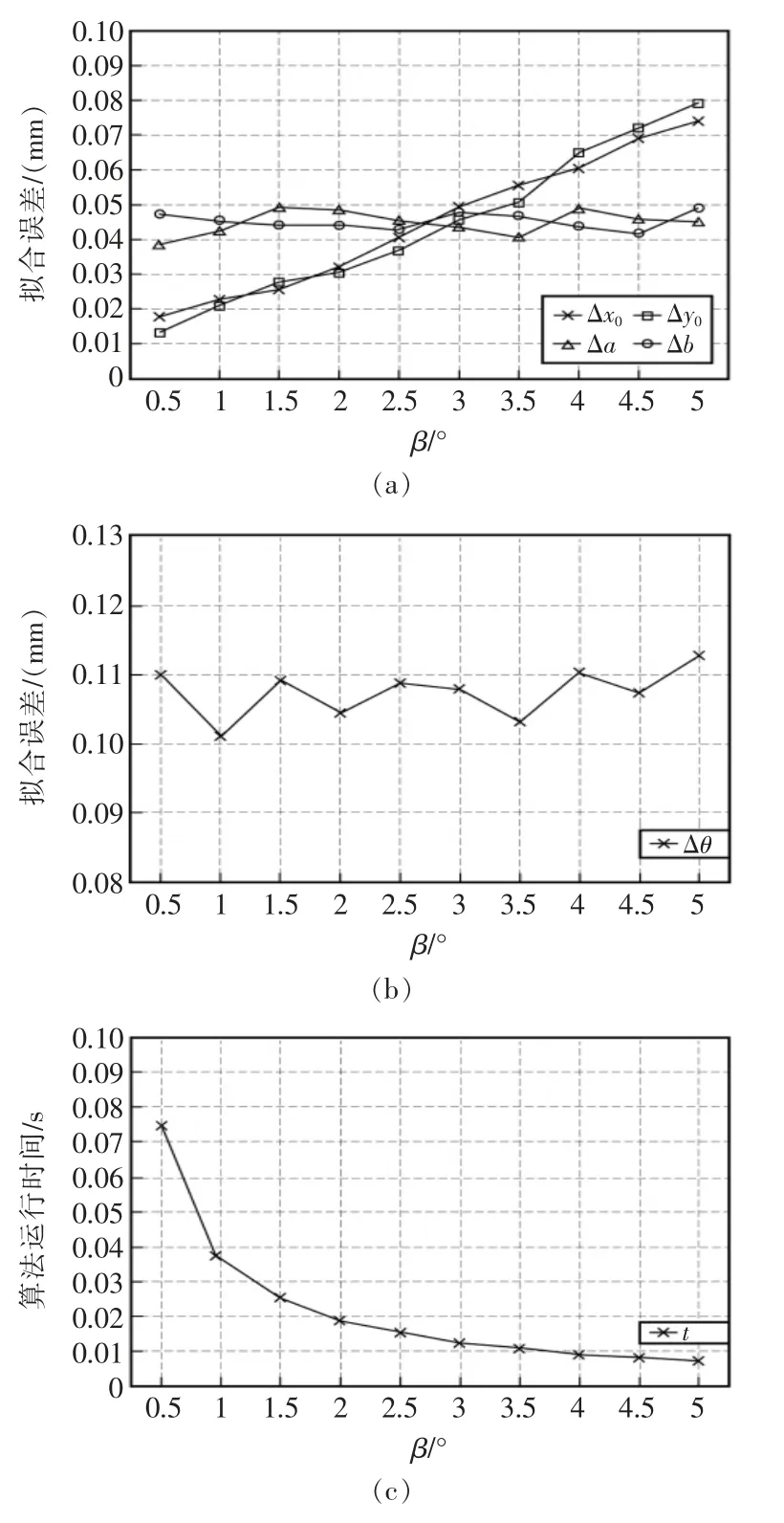
图9 拟合误差曲线Fig.9 Fitting error curve
算法在计算椭圆长半轴长、短半轴长、方向角时采用了二分法进行迭代计算提高了拟合精度,因此长半轴长误差、短半轴长误差、方向角误差不会受到旋转角步长变化的影响,最大拟合误差分别为0.049 mm、0.049 mm、0.113°,通过二分法可以快速缩小迭代范围,以达到快速、精确测量的目的。
5 结语
本文提出了一种基于几何对称性的椭圆拟合算法,通过利用椭圆的中心对称的性质及二分迭代逼近方法,计算出椭圆中心坐标,不断逼近椭圆长短半轴长、方向角的实际值。此算法的优点在于:可以通过控制切线的旋转角步长,及迭代阈值分别对椭圆的中心坐标、长短半轴长的拟合精度进行调整,在达到拟合精度的同时,最大限度提升了拟合效率。拟合结果可达到项目中零件检测精度要求,经验证可投入实际运用。
——对2018年广州市一道中考题的研究

