基于有限元的变压器流场及温度场仿真分析

李 涛，孙学武，杜晓平，宋媛媛

（国网山东省电力公司，济南250000）

有限元是一种求偏微分方程边值问题近似解的数值方法，分解整个问题区域为不同的子区域，每个子区域都是一个简单的部分，这个简单的部分就是有限元[1]。

基于有限元分析变压器流场，该变压器的流场是指变压器内的压强变化，基本的流场形式共有3种类型。第一种是变压器内有相对均匀、略有弯曲的流线组成的气流；第二种变压器流场类型呈现出奇异线的形式，也就是变压器内的风向呈现出不连续的间断线或是分支汇合的渐近线形式[2]；第三种形式则是变压器中风速为零。变压器中的流场所在区域是运动流体所占有的空间。变压器系统内各个点的温度集合称为温度场，反应了变压器温度在空间和时间上的分布。分析基于有限元的变压器流场及温度场，可以增强电网的可靠性，保证电网的安全运行。关于变压器流场和温度场的模拟，相关学者做了大量研究。

文献[3]提出基于CFDesign 的油浸式深海变压器流场和温度场仿真模拟，首先参考环境湿度、海洋环境、深海海水流速等变化因素，进行基于CFDesign 的油浸式深海变压器流场和温度场的数值评估。在评估结果基础上，计算指导变压器的流程，完成深海变压器流场和温度场的模拟。文献[4]提出12 kV 中压开关柜电磁-热流场耦合仿真，首先，在整个开关柜的仿真分析中，基于涡流场、气流场和温度场理论，对开关柜在自然对流和强迫对流条件下的温升分布进行了仿真分析。然后，针对开关柜中出现的温升问题，提出了几种改进方法，包括采用弹簧接触指状结构代替柔性连接结构，以及真空断路器（VCB）极和电流互感器（CT）的优化方案。然后，基于电磁-热流场耦合方法，对不同的改进方案进行了仿真研究。虽然上述研究取得一定进展，但是在有限元方面的研究尚且不足，为此提出基于有限元的变压器流场及温度场仿真分析。首先根据变压器内实际的电磁特征描述流场中对应边值，计算变压器流场仿真参数。然后使用离散化处理变压器产生的涡流，得到变压器绕组的流场仿真参数。计算变压器温度场各状态下的损耗热量，使用整场离散、整场求解方法得到温度场仿真参数，实现变压器流场及温度场的模拟仿真。最后设置仿真实验，得出有效性结论。

1 基于有限元的变压器流场及温度场仿真分析

1.1 计算变压器流场仿真参数

确定变压器流场仿真参数时，首先根据流场的基本理论，保持变压器的正常工作，针对如图1所示的变压器进行仿真模拟。

图1 实际运行的变压器Fig.1 Transformer in operation

在变压器正常运行过程中存在这一规律：若变压器流场存在海量样本满足排列集中分布的情况，此时变压器流场可采用可控调压模式[5-6]；这种方法不会用于特征的全部样本值；若变压器流场存在海量样本满足排列集中分布各不相同的情况，可针对变压器流场进行流场数值模拟控制。结合变压器的实际电磁特征，描述流场内对应边值为高压侧与中压侧，高压侧如式（1）所示：

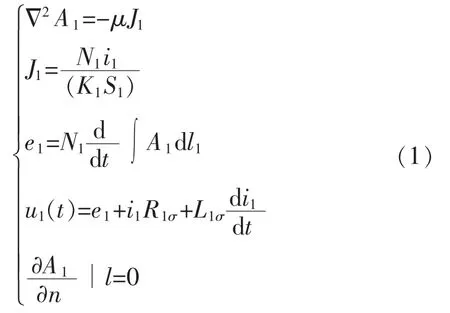
得到中压侧如式（2）所示：

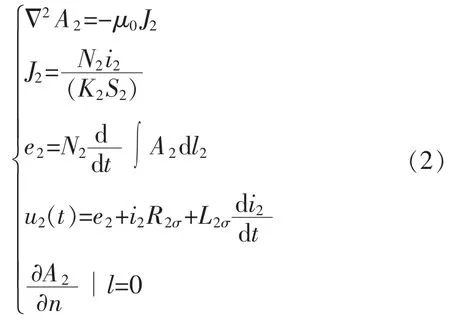
式中：A 为磁矢位；J 是电流密度；e 表示感应电动势；N 表示线圈匝数；K 为占空比；Rσ是等效电阻；Lσ是等效漏电电感；μ 是线路阻抗；i 为线路负载。对式（1）、式（2）进行离散化处理，得到变压器的正弦稳态场的定解方程如式（3）所示：

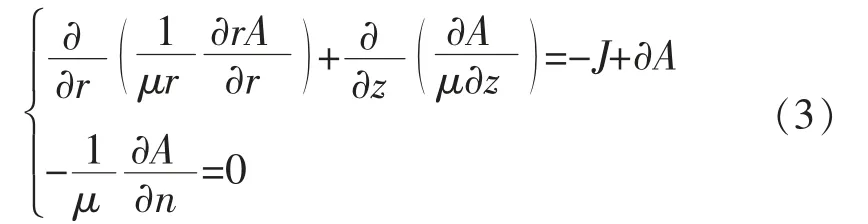
式中：A 为向量磁位；σ 为电导率；μ 为磁导率；J 为源电流密度。在变压器的正弦稳态场的定解方程的支持下，不同属性的重要程度的排序与变压器中各个节点位置的创建可基于有限元特征分配来实现[7-8]。再将图1运行的变压器的调压形式转换为无励磁旁柱调压，保持中高压的运行状态，计算得到变压器仿真参数如表1所示。

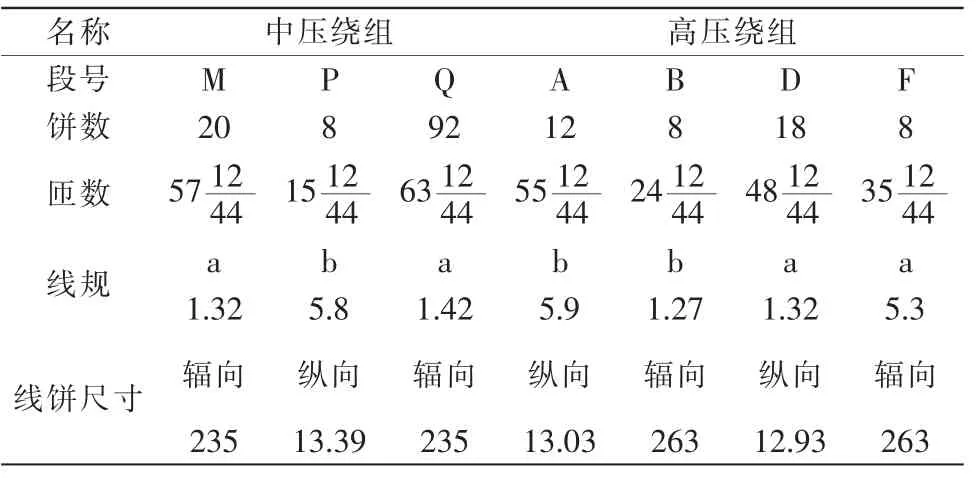
表1 计算得到的变压器仿真参数Tab.1 Calculated transformer simulation parameters

在计算得到表1中的流场仿真参数后，确定变压器换热特性，利用有限元处理方法，模拟仿真变压器的流场以及温度场两种特性。

1.2 确定变压器温度场仿真参数

在确定变压器流场仿真参数的基础上，需确定变压器温度场仿真参数。首先计算电力变压器损耗转化成的热量[9]，使用傅里叶导热定律计算变压器转化的热量，得到：

式中：Φ 表示单位时间内通过截面的热量；T1，T2表示发生热传导的两物体表面各自的温度；x 表示发生热传导的距离；S 表示表面积；k 为热传导系数。使用式（4）计算变压器温度仿真参数，单位热流密度q，得到：

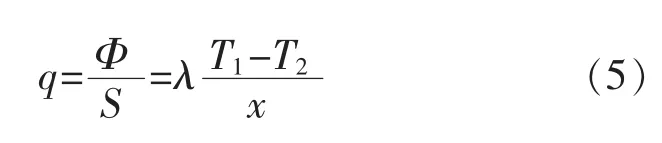
在变压器中若出现负载不平衡，容易引起三相不平衡，即三相电压或电流的值不相等或频率不同。电力变压器油在流经其内部铁芯、绕组和金属表面构件时，变压器内部会产生对流换热作用，致使变压器周围的油温度升高[10-12]。所以在计算温度场仿真参数时，改变变压器内的固有温度场，计算出的温度场仿真参数，依据牛顿对流换热公式得到式（6）：

式中：Tw，Tf分别为壁面温度和流体温度；h 表示变压器传热导数。变压器内部不相邻的固体元件之间会发生辐射传热和电力变压器油箱向外界空气的辐射传热的情况[13]，计算两种热辐射反应的仿真参数，计算公式如式（7）所示：

式中：Φ1是表面1 以热辐射形式与表面2 的对流热量；S1为发生表面1 的表面积；T1，T2为发生表面1和表面2 的温度；ε 为物体1 的黑度；C0为黑体辐射系数。联立上式温度场内温度变化的表达式，得到温度场仿真参数控制方程如式（8）所示：

式中：T 为温度；k2是变压器油和变压器固体域的导热系数；∂为变压器油的比热容，qA为变压器固体域的热流密度。使用整场离散、整场求解方法对式（8）进行数值计算，得到变压器温度场仿真模拟参数[14-15]。将变压器温度场的耦合界面作为内边界，实际求解参数的推导过程如图2所示。

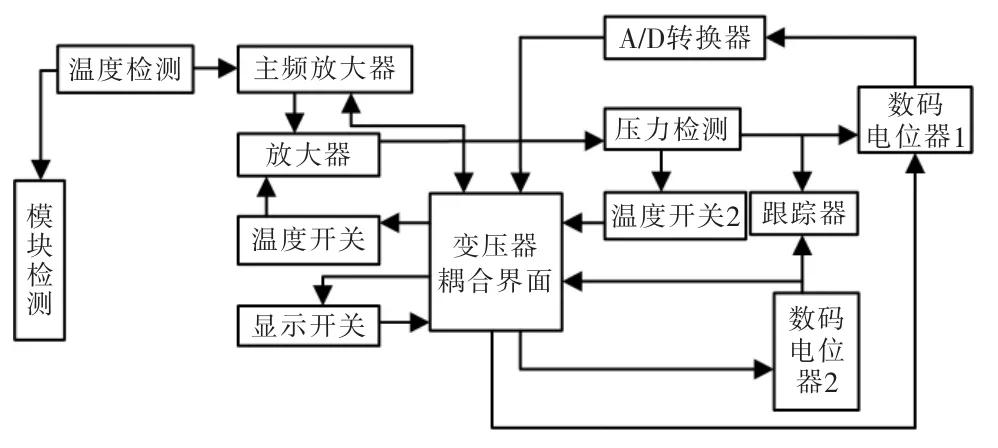
图2 仿真参数求解推导过程Fig.2 Simulation parameter solution derivation process

由图2的推导过程可知，在变压器耦合界面进行温度场控制，其变压器可获得各项指标在考察周期内对应的评估效果。可在变压器控制容积内对式（8）积分计算，得到：

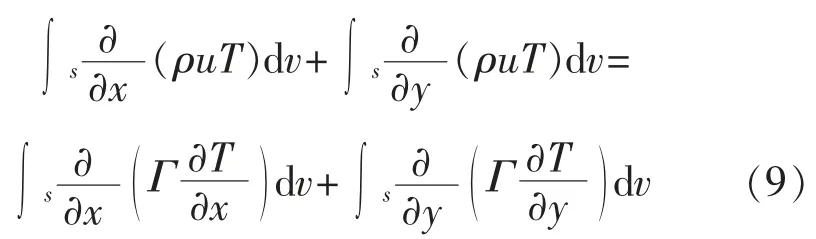
式中：Γ 为广义的扩散系数；S 为广义的源项；u 为速度矢量U 在x，y 轴上的速度分量。使用调和平均插值法分析式（9），令图2中的耦合界面作为变压器中心的控制容积，以点W 为中心控制容积的热流密度，利用Fourier 定律热流密度仿真参数：

式中：q1为热流密度；Γw为交界面处的扩散系数。使用式（10）计算最终得到温度场变压器的所有仿真参数，然后利用有限元法模拟仿真变压器流场及温度场。

1.3 利用有限元法模拟仿真变压器流场及温度场

在模拟仿真变压器流场及温度场时，首先分析变压器内部构件遵守的质量、动量和能量的守恒，计算变压器内部的质量守恒，得到：

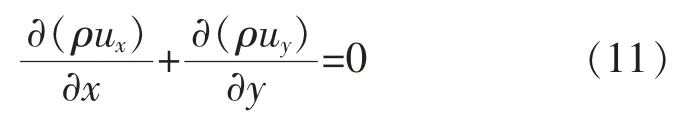
式中：ρ 为变压器内的流体密度；ux，uy分别是单位体积内流体的径向和轴向流速[16]。结合流场及温度场的仿真参数表达式，计算出稳态不可压缩流体的控制方程，得到：

式中：f 是散热系数；η 为温度函数；U 为变压器内的电压[17-18]。结合不可压缩流体的控制方程，使用有限元法将流场及温度场使用同一种参数进行模拟仿真，得到：

在温度场稳定时，在仿真温度场时可表示为

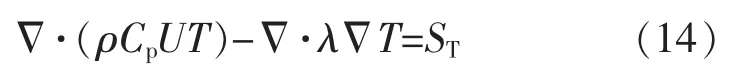
式中：λ 为热传导率；ST是单位体积的产热率；Cp为定压比热容。所以在上式中，当式（13）中的流体的速度为0 时，此时式（13）可以统一模拟仿真变压器的流场[19]。当设置变压器区域内的固体速度为0 时，使用式（14）即可仿真得到变压器内的温度场[20]，依次迭代计算出流场及温度场的有限元控制方程式（13）和式（14）。

2 仿真实验

为了验证基于有限元的变压器流场及温度场的效果及可行性，设置仿真实验。准备640*480 红外像素画质、IFOV 参数为0.93 mRad、最小检测目标尺寸在0.14 mm、测温范围在-20 ℃～650 ℃的热成像仪进行实验。划定变压器的功能区域，规定流场方向，标定热点位置，得到变压器区域示意图如图3所示。

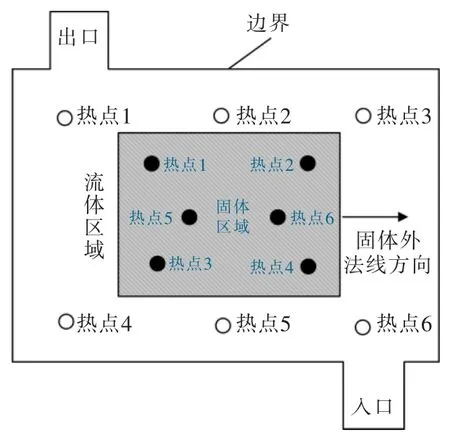
图3 变压器划分区域示意图Fig.3 Schematic diagram of the divided area of the transformer

使用图3的划定区域以及标记的6 个热采集点，分别为热点1 到热点6，在固体区域和流体区域分别都有6 个热采集点。使用基于有限元的变压器流场及温度场仿真方法，模拟仿真变压器内的流场及温度场特性，仿真流程如图4所示。

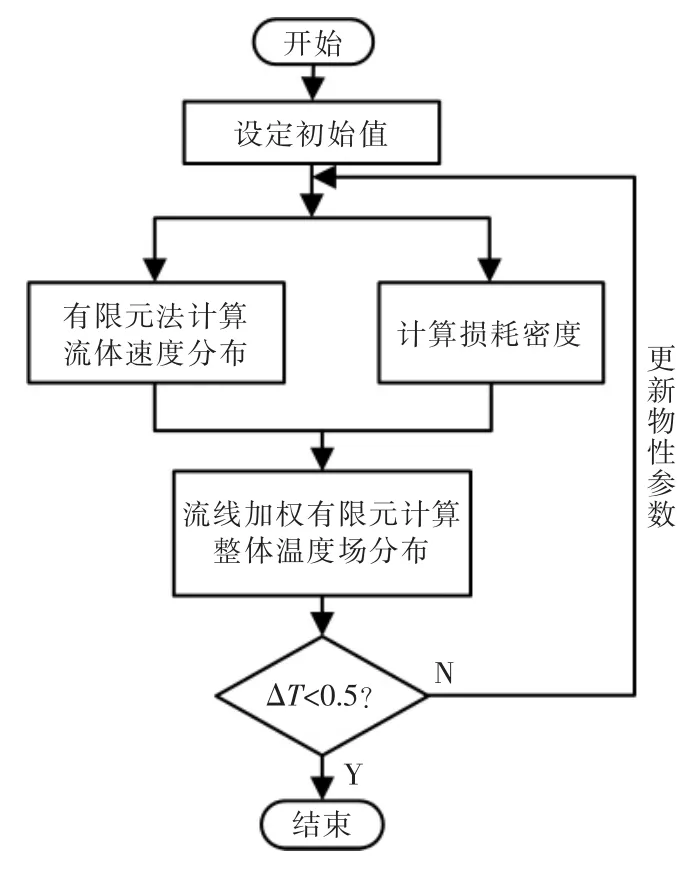
图4 流场温度场仿真流程Fig.4 Flow field and temperature field simulation flow chart

使用图4的耦合仿真流程，利用流线加权有限元法，实现利用相同的变量参数模拟仿真变压器流场及温度场，流场中的导线会感应到变压器内部的电动势，产生涡流，最终得到的模拟仿真结果如图5所示。

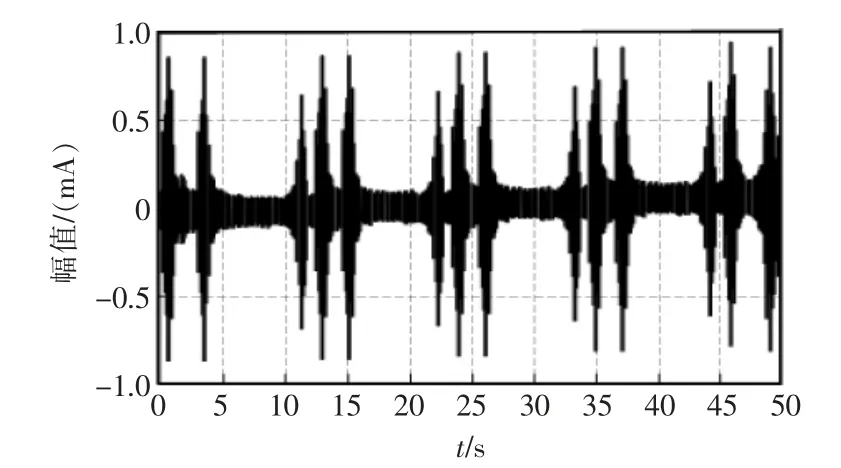
图5 基于有限元的变压器流场及温度场仿真结果Fig.5 Simulation results of transformer’s flow field and temperature field based on finite element

由图5可知，是利用计算出的流场及温度场的仿真参数最终得到的仿真结果，模拟仿真后的变压器整体流场呈现出上下对称分布，温度流场间的电压绕组和中压绕组之间的主空道为温度场的通道。为进一步验证本文方法的可行性，对比文献[3]方法和文献[4]方法仿真结果是否出现缺失，使用3 种模拟仿真方法最终得到仿真结果如图6所示。

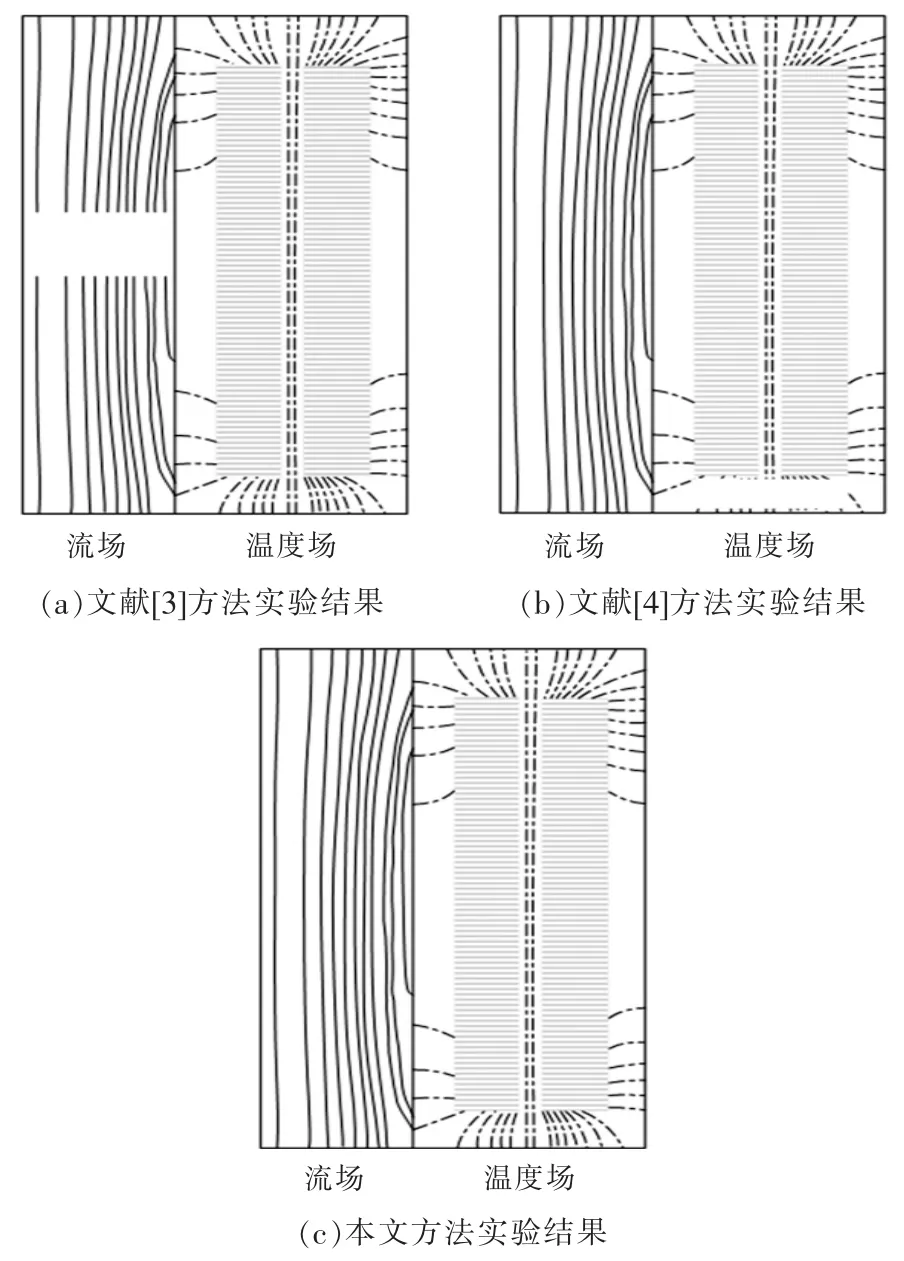
图6 三种方法的变压器流场及温度场仿真实验结果Fig.6 Simulation results of three methods of transformer’s flow field and temperature field

由图6的3 种方法的变压器流场及温度场仿真实验结果可知，文献[3]方法在仿真变压器流场及温度场时，流场的仿真结果发生缺失，文献[4]方法在实际仿真变压器流场及温度场时，温度场的仿真结果会发生缺失，而使用了本文基于有限元的变压器流场及温度场仿真方法可以同时仿真出变压器的流场及温度场，仿真结果不发生缺失，更适合实际模拟仿真变压器流场及温度场。实验研究结果表明，本文方法的变压器流场及温度场仿真结果更加有效。

3 结语

我国输变电技术的不断发展，电力变压器的电压能力和容量技术也不断提高，社会生产与生活所需的变压器是采用高压输电的方式进行输送，逐级变压得到的。伴随社会生产力与生产水平的进步，人们对于电力质量、电力数量要求越来越高，变压器作为关键性设备，其安全与否涉及到整个电力系统的稳定性与可靠性，这就要求对变压器进行定期检查与维修，保证其性能不断优化与提高。分析变压器的流场及温度场也就成为了电力发展中的重要问题。本文方法的创新点是分析变压器内部构件遵守的质量、动量和能量的守恒，计算变压器内部的质量守恒。模拟仿真变压器内的流场及温度场可以有效的预测变压器的容量和内部热点温度，提高变压器的热性能和使用寿命，降低事故的发生几率，在实际的应用中具有一定的借鉴价值。对于未来的工作，可就如何减少变压器流场及温度场的控制操作时间进行更加深入的研究。