基于模糊控制的永磁同步电机滑模观测器控制

柯希彪，郭 琳，3，袁训锋，陈 垚，徐晓龙

（1.商洛学院 电子信息与电气工程学院，商洛726000；2.商洛市分布式新能源应用技术研究中心，商洛726000；3.西安交通大学 电力设备电气绝缘国家重点实验室，西安710049）

永磁同步电机PMSM（permanent magnet synchronous motor）具有结构简单、体积小、能量密度高等优点，在现代制造业等众多领域应用十分广泛[1-2]。永磁同步电机控制中检测出电机实时转子位置信息和转速信息是决定电机控制的成败和控制性能的关键因素。无传感器控制检测电机转子相位和转速信息价格低、控制系统可靠性较高，因此成了众多学者研究的重要课题。

1 永磁同步电机滑模控制的应用

滑模观测器控制SMO（sliding mold observor）具有结构简单、抗干扰能力强、可靠性高等优点，被广泛应用于永磁同步电机控制系统中。文献[3-5]通过构建滑模观测器模型检测电机转速和相位，实现了永磁同步电机无传感器控制，控制结果良好。文献[6-7]结合模糊控制理论，设计模糊滑模观测器控制模型，通过设计模糊控制调节滑模控制参数，实现了永磁同步直线电机无传感器控制，较传统滑模控制性能优良。文献[8-9]研究了滑模观测器控制产生抖振的原因，设计饱和函数对传统滑模观测器进行优化，仿真分析和实验结果表明改进后的滑模观测器能够较准确检测出电机转速，并且对滑模控制的抖振有明显削弱。文献[10]设计了一种积分滑模控制算法对六相永磁同步电机进行控制，通过仿真验证了该控制策略具有良好的控制性能。文献[11]设计了一种模糊自适应反步积分滑模控制策略，试验证明该控制策略对电机控制具有较强的抗干扰能力。文献[12]将模型参考自适应控制与模糊控制相结合，该控制策略有效提高了模型参考自适应控制的自适应能力。文献[13]提出了一种模型参考自适应控制，通过对PI 控制参数进行实时调节，有效提高了模型参考自适应控制性能。文献[14]设计了一种分段PI 模型参考自适应控制，通过实验证明该控制策略可以实现电机全速范围内的无传感器控制。文献[15]设计滑模模型参考自适应控制策略，将双正切函数引入滑模控制中，有效地抑制了滑模控制抖振，准确地检测出了电机转子相位信息。

通过对永磁同步电机传统滑模观测器控制策略的研究，结合模糊控制的特点，在此设计了一种模糊滑模观测器控制。模糊控制具有较强的自适应能力，滑模控制具有较强的抗干扰能力。设计积分滑模面，模糊控制实时调节滑模参数，将饱和函数引入滑模控制中进行观测器设计，可以有效抑制滑模控制抖振，提高观测器检测精度。通过建立模糊滑模观测器控制模型进行验证，结果表明所设计的控制策略可以较好地实现永磁同步电机控制，控制性能优良。

2 永磁同步电机控制模型

隐级式PMSM 两相旋转坐标方程[2-4]为

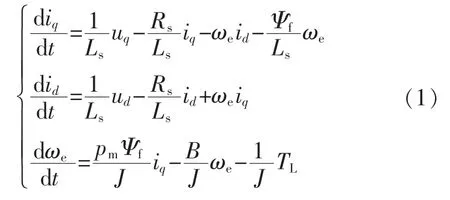
式中：iq，id为电机交、直轴电流分量；uq，ud为电机交、直轴电压分量；Rs为定子绕组等效电阻；Ls为电枢绕组等效电感；pm为转子磁极对数；ωe为电角频率；Ψf为转子励磁磁链；J 为转子转动惯量；B 为转子黏滞系数；TL为电机负载转矩。

PMSM 磁链方程[2-4]为

式中：Ψq，Ψd分别为电机交、直轴磁链。

PMSM 电磁转矩方程为

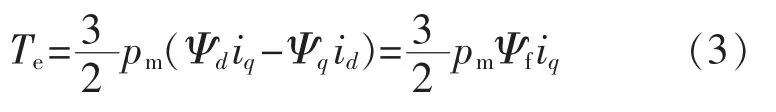
永磁同步电机控制是以矢量控制模型进行设计的，矢量控制控制精度较高，结构简单，是一种无差控制策略，在永磁同步电机控制领域中应用较为广泛。

3 永磁同步电机滑模观测器设计

PMSM 在静止坐标系（α-β 轴）的模型为[2-4]为

式中：iα，iβ为电机α，β 轴电流分量；uα，uβ为电机α，β 轴电压分量；eα，eβ为α，β 轴反电动势；θe为电机转子相位。

滑模观测器模型设计为

式中：“^” 代表各状态量估算值；Hα，Hβ分别为对应分量的控制律。

式（6）式（4）求差可得滑模观测器状态方程为

设计观测器积分滑模面，即

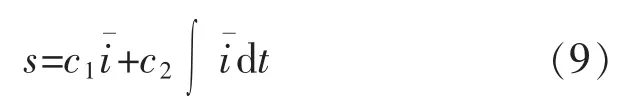
其中，c1＞0，c2＞0。

滑模观测器采用指数趋近律，即

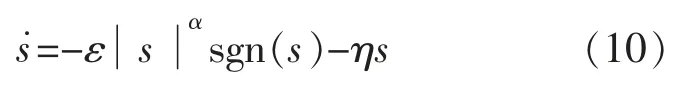
其中，ε＞0，η＞0，0＜α＜1。

滑模观测器控制律为

其中

系统达到稳定运行状态时，状态变量及其变化率均为0，即

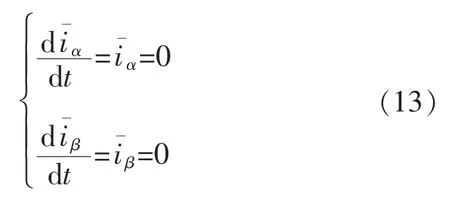
PMSM 反电动势模型为

建立Lyapunov 方程，即

对式（15）求导，可得

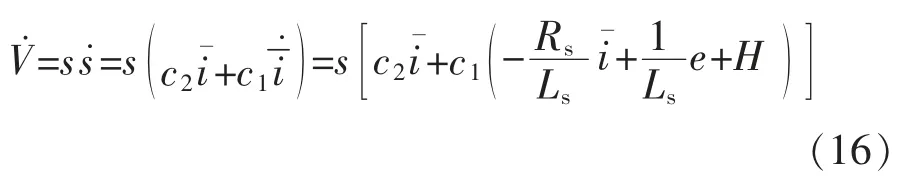
故

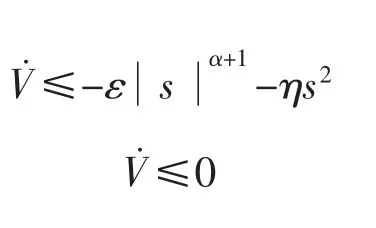
由此证明所设计积分滑模观测器满足Lyapunov稳定性条件，设计的观测器趋于稳定，可实现永磁同步电机滑模控制。

为减小符号函数引起的系统抖振，构建线性饱和函数设计滑模控制率，饱和函数模型为

式中：a 为正常数，其值决定饱和函数线性区域内滑模增益的斜率和滑模边界层厚度。当γ 取值满足式（12）时，滑模观测器依然满足Lyapunov 稳定性条件。

滑模观测器控制律可改写为

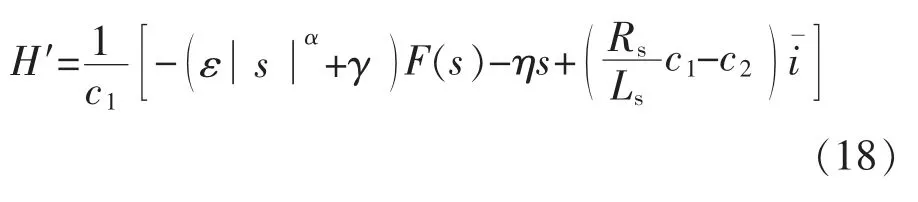
4 模糊滑模观测器设计

模糊控制是一种利用模糊化概念实现精确控制的智能控制策略，模糊控制的鲁棒性和自适应能力较强。在此，将模糊控制理论引入滑模控制中设计模糊滑模观测器控制策略，以电机控制系统的状态变量为模糊控制的输入变量，模糊控制的输出变量为滑模控制参数，设计模糊控制规则，通过实时调整滑模观测器参数，有效提高滑模观测器控制性能。

图1 输入变量隶属函数曲线Fig.1 Membership function curve of input variable

图2 输出变量隶属函数曲线Fig.2 Membership function curve of output variable

表1和表2中，大写字母分别表示模糊条件：NB为负大，NM 为负中，ZE 为零，PM 为正中，PB 为正大，S 为小。由模糊规则拟合的变量c1和c2所输出的特性曲面如图3所示。

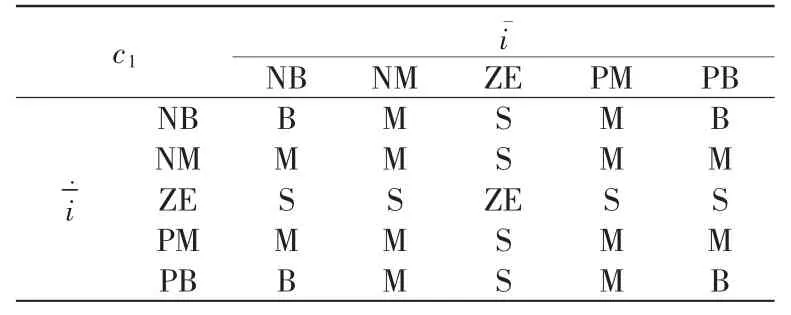
表1 输出变量c1 的模糊规则Tab.1 Fuzzy rules of output variable c1

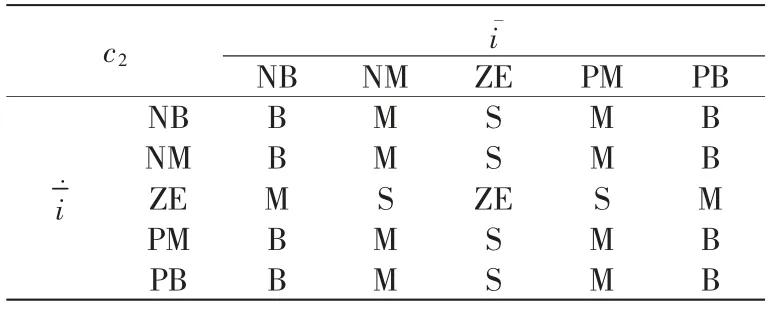
表2 输出变量c2 的模糊规则Tab.2 Fuzzy rules of output variable c2

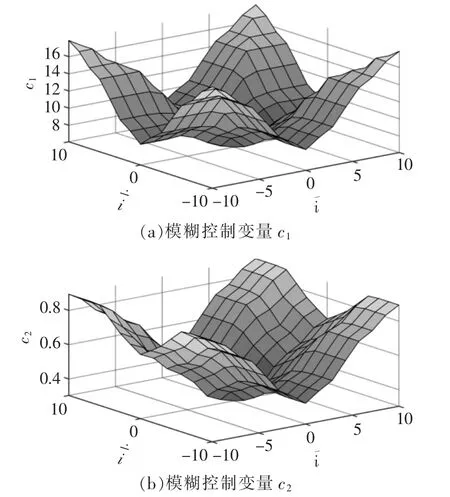
图3 模糊控制变量的特性曲面Fig.3 Characteristic surface of fuzzy control variables

永磁同步电机控制模型如图4所示。

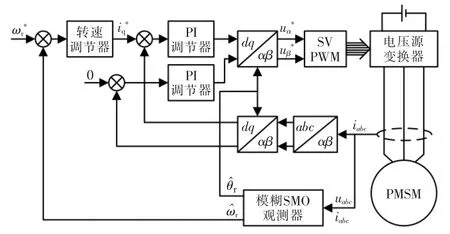
图4 PMSM 控制模型Fig.4 PMSM control model

5 仿真验证

搭建永磁同步电机控制模型，将设计的模糊滑模观测器控制同传统滑模观测器控制进行仿真对比，使电机在相同的运行工况下、相同的系统参数下运行，验证设计的观测器控制能够满足预定控制要求。

永磁同步电机参数见表3，电机调试最高转速为2000 r/min，取滑模观测器参数γ=110。

表3 PMSM 参数Tab.3 PMSM parameters

分别搭建传统滑模观测器控制和模糊滑模观测器控制模型进行永磁同步电机控制。电机运行时间均设定为0.2 s，电机的起始转速设定为n=0 r/min，在t=0 s 时刻电机转速设定为1000 r/min；当电机运行至t=0.06 s 时刻，电机转速调节至n=2000 r/min；在t=0.14 s 时刻，为电机突加TL=1 N·m 的负载转矩。电机仿真波形分别如图5—图8所示，其中图5和图6为电机转速波形，图7和图8为电机转子相位波形。

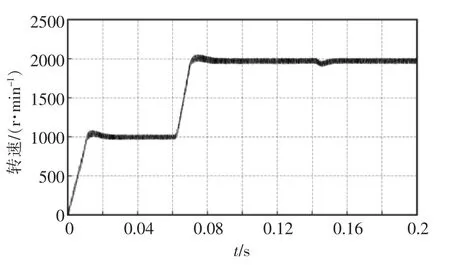
图5 PMSM SMO 转速波形Fig.5 PMSM SMO speed waveform

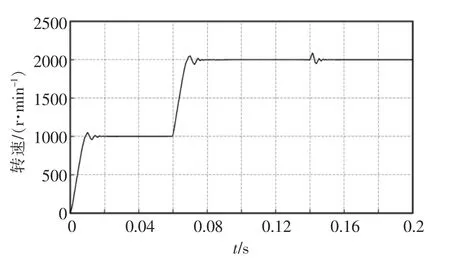
图6 PMSM 模糊SMO 转速波形Fig.6 PMSM fuzzy SMO speed waveform

图7 PMSM SMO 相位波形Fig.7 PMSM SMO phase waveform

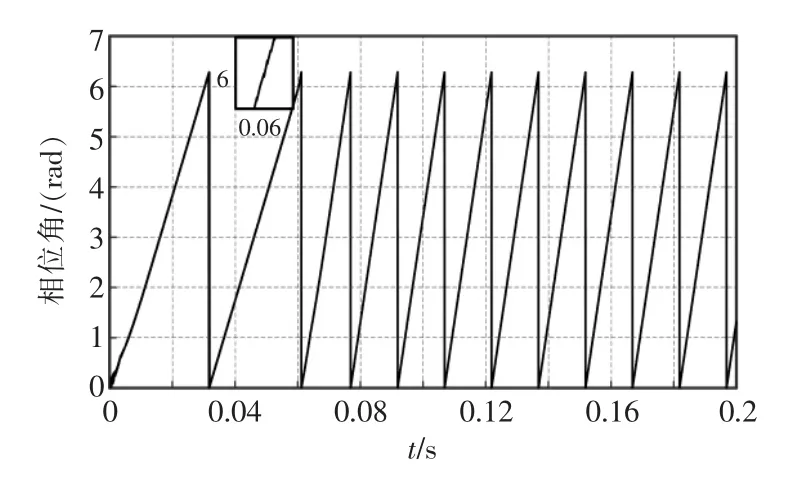
图8 PMSM 模糊SMO 相位波形Fig.8 PMSM fuzzy SMO phase waveform

通过对比图5与图6可见，电机转速在调节过程中（t=0 s 和t=0.06 s 时刻），转速均可以快速跟踪并达到预定转速，体现了滑模控制的快速响应能力。然而，无论是传统滑模观测器控制还是模糊滑模观测器控制，电机转速均会出现较大的超调量。

在传统滑模观测器控制中，电机转速超调量持续时间比较长，电机转速波动比较大。在模糊滑模观测器控制中，电机转速超调量在持续振动1～2 个振动周期后，转速趋于稳定值，且电机在稳定态运行下转速比较平稳，几乎不会出现转速波动的情况（如图6所示）。当给电机突加负载时（t=0.14 s 时刻），电机转速会出现一定的抖动，模糊滑模观测器控制的转速波形，在转速波动一两个振动周期后依然会趋于稳定值，而传统滑模观测器控制的转速会持续的振动，不会达到一个稳定值（如图5所示）。由此表明，模糊滑模观测器控制较传统滑模观测器控制，具有较强的抗干扰能力和自适应能力。

对照图7与图8可见，传统滑模观测器检测电机相位存在较大幅度的振动，电机相位检测误差较大；模糊滑模观测器对电机相位检测的精度较高，检测的电机相位抖振比较小（t=0.06 s 时刻），为电机控制交直轴电流解耦提供可靠的保障，使电机控制更精确，系统稳定性更高。通过仿真证明，模糊滑模观测器控制在永磁同步电机控制中，表现出了更好的控制性能。

6 结语

通过对永磁同步电机滑模观测器控制研究，结合模糊控制，设计了模糊滑模观测器控制策略。该积分滑模控制具有抗干扰能力强，控制稳定性高的优点，模糊控制具有较强的鲁棒性和自适应能力。将模糊控制与积分滑模控制相结合，可以提高滑模观测器的检测电机转子信息的精度，降低滑模控制的抖振，同时使得控制系统的抗干扰能力和自适应性均有所提高。通过仿真对比验证了提出的模糊滑模观测器控制是有效的。