踩点答对题 自信得满分

文 周汉斌

（作者单位：江苏省东台市实验中学）

中考要想取得高分，攻克最后的两道综合题是关键。其中，几何综合题一般分三小题呈现，满分12分。近年来，这类题往往以动态几何形式出现，在图形的变换过程中，探究图形中某些不变的因素，把操作、观察、探求、计算和证明融合在一起。在答题时我们要调节好心态，心中默念“压轴题不需要拿满分，但要拿到能拿到的分”。下面以2019年济南中考第26题为例分析说明。

小圆同学对图形旋转前后的线段之间、角之间的关系进行了拓展探究。

（一）猜测探究

在△ABC中，AB=AC，M是平面内任意一点，将线段AM绕点A按顺时针方向旋转与∠BAC相等的角度，得到线段AN，连接NB。

（1）如图1，若M是线段BC上的任意一点，请直接写出∠NAB与∠MAC的数量关系是________，NB与MC的数量关系是 ；

图1

（2）如图2，点E是AB延长线上一点，若M是∠CBE内部射线BD上任意一点，连接MC，（1）中结论是否仍然成立？若成立，请给予证明，若不成立，请说明理由。

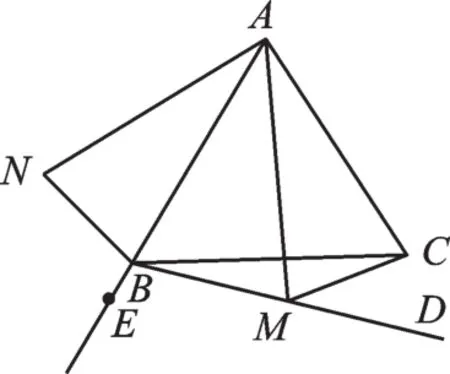
图2

（二）拓展应用

如图3，在△A1B1C1中，A1B1=8，∠A1B1C1=60°，∠B1A1C1=75°，P是B1C1上的任意点，连接A1P，将A1P绕点A1按顺时针方向旋转75°，得到线段A1Q，连接B1Q。求线段B1Q长度的最小值。

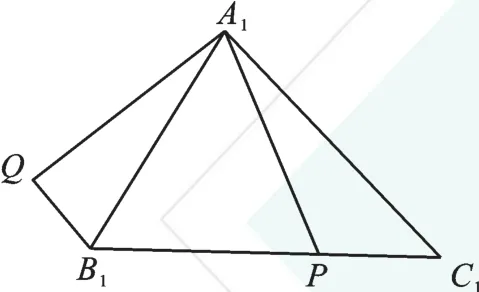
图3

此题位于整卷倒数第2题的位置，是考查几何变换的一道综合题，有较大的难度，也是一道区分度明显的压轴题，解答的原则是分步取分。

【分析（一）（1）】如图1，

∵∠MAN=∠CAB，

∴∠NAB+∠BAM=∠BAM+∠MAC，

∴∠NAB=∠MAC。

∵AB=AC，AN=AM，

又∠NAB=∠MAC，

∴△NAB≌△MAC（SAS），

∴BN=CM。

故答案为∠NAB=∠MAC，BN=CM。

【点评】填对一空得2分，两空共4分，压轴题不是每一个问题都很难，认真读题审题，思考一下，还是能轻松拿分的，解题的自信很重要。

【分析（一）（2）】（1）中结论仍然成立，第（2）问的证明方法也与（1）类似，（1）是为（2）引路的。

如图2中，（1）中结论仍然成立。

理由：∵∠MAN=∠CAB，

∴∠NAB+∠BAM=∠BAM+∠MAC，

∴∠NAB=∠MAC，

又∵AB=AC，AN=AM，

∴△NAB≌△MAC（SAS），

∴BN=CM。

【点评】一道试题有几个小题，题目之间必然有关联，如本题的（1）（2）两问之间是呈现递进关系的，（1）是（2）的特例，（2）是（1）的一般情况，因此做（2）时不妨看看（1），（1）（2）比一比，思路自然产生。

【分析（二）】题目明确指出：“拓展应用”，也就是利用（一），解决（二），因此我们就要在（二）中寻找（一）的影子，一旦找出，（二）就不难解决了。（一）中的△ABC是等腰三角形，因此我们在A1C1上截取A1N=A1B1，连接PN，如图 4，出现了（一），模仿之：

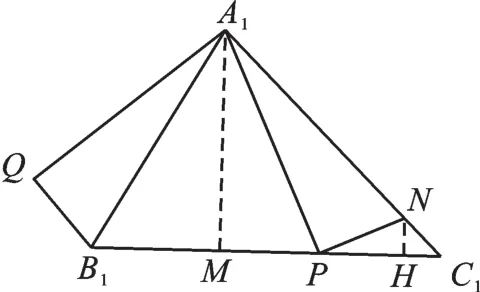
图4

∵∠C1A1B1=∠PA1Q，

∴∠QA1B1=∠PA1N，

又∵A1Q=A1P，A1B1=AN，

∴△QA1B1≌△PA1N（SAS），

∴B1Q=PN。

要求线段B1Q长度的最小值，则转化为求PN长度的最小值。联想到垂线段最短，即当PN垂直B1C1时PN的值最小。为此作NH⊥B1C1于H，作A1M⊥B1C1于M，如图5。

在Rt△A1B1M中，

在 Rt△NHC1中，

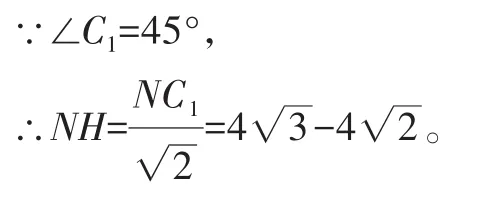
根据垂线段最短可知，当点P与H重合时，PN的值最小，

∴QB1的最小值为。

图5

【点评】最后的4分，是全题的亮点。将A1P绕点A1按顺时针方向旋转75°，得到线段A1Q。动点Q由点P的运动而发生，点P动则点Q动，点P是主动点，点Q是从动点，因此点P在线段B1C1上运动，点Q也应该在某线段上运动。点Q是由点P绕点A1按顺时针方向旋转75°得到的，因此点Q的路径是线段B1C1绕点A1按顺时针方向旋转75°得到的（如图5）。要求线段QB1的最小值，由于点B1的位置是确定的，而点Q的路径是一条线段，线段最小值当然是根据垂线段最短来确定，但这个最小值如何求，则难以下手。题目的“拓展应用”暗示我们去构造（一）中的模型，利用（一）的结论解决问题。根据这个暗示，不难添加辅助线，构造全等三角形转化问题。我们要善于揣摩命题者的意图，寻找命题专家不经意中透露的信息，一旦想到暗语，压轴题也是不难破解的。