抓关键 巧解题
文 王娟玲
(作者单位:江苏省无锡市东实验学校)
“统计与概率”与我们的生活密不可分。如果我们在生活中学会用数学的眼光来分析问题,就会发现很多乐趣。不信,我们就一起来看看。
例1在一次捐款活动中,某班50名同学都拿出自己的零花钱,有捐5元、10元、20元的,还有捐50元和100元的,如图所示的统计图反映了不同捐款数的人数比例。那么根据图中信息,该班同学平均每人捐款______元,捐款的众数是______元,中位数是______元。
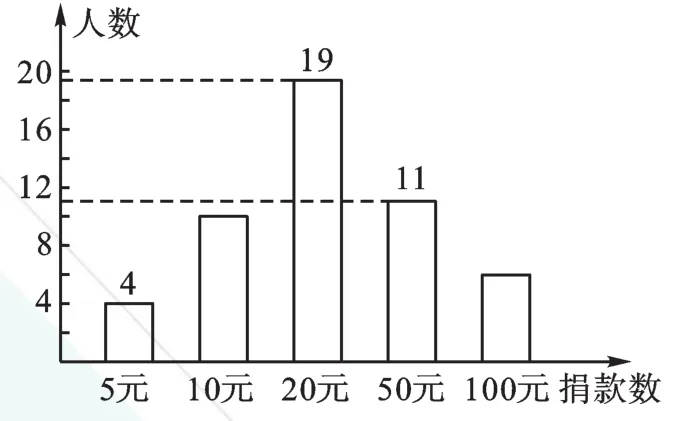
图1

图2
【分析】本题的关键是:根据图1中捐款20元的人数是19人和图2中捐款20元人数占总人数的38%解决问题。求得总人数:19÷38%=50(人)。进而求得捐款100元的人数:50×12%=6(人)。最后求得捐款10元的人数:50-(4+19+11+6)=10(人)。平均每人捐款数=总金额÷总人数。同学们要避免将5个数的算术平均数认为平均每人捐款数。根据众数的定义,捐款的众数为20元。在求解中位数时,一定要牢记将数据先排序。总人数为50,中位数取的是第25和第26人捐款面值的平均数,这两个同学捐款数均为20元,所以中位数也是20元。
答案:33,20,20。
例2一只不透明的袋子中装有2个白球和3个红球,这些球除颜色外其他都相同,搅匀后从中任意摸出1个球。
甲说:“摸出的球不是白球就是红球,所以摸出白球和摸出红球这两个事件是等可能的。”
乙说:“白球有2个,红球有3个,所以摸出白球和红球这两个事件不是等可能的。”
你认为谁的说法有道理,请说明理由。
【分析】本题关键在于对“等可能性事件”的理解。袋子里共有5个球,所以摸出每个球是等可能的。由于有2个白球和3个红球,所以乙的说法正确。
解:乙有道理,摸到每一个白球和每一个红球是等可能的,摸出白球的可能性比摸出红球的可能性小。
例3甲、乙两超市(大型商场)同时开业,为了吸引顾客,都举行有奖酬宾活动:凡购物满100元,均可得到一次摸奖的机会。在一个纸盒里装有2个红球和2个白球,除颜色外其他都相同,摸奖者一次从中摸出两个球,根据球的颜色决定送礼金券的面值(在该超市使用时,与人民币等值),如下表:
甲超市:
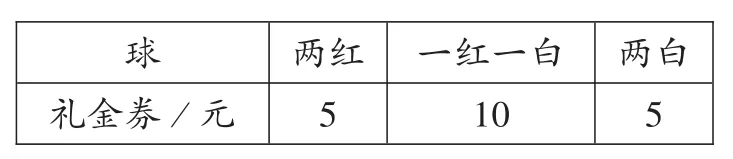
礼金券/元球两红5一红一白10两白5
乙超市:

两白10球礼金券/元两红10一红一白5
如果只考虑中奖因素,你将会选择去哪个超市购物?请说明理由。
【分析】理清题意,选择去某个超市购物的原因在于平均获得的礼金券面值多,这就需要我们计算摸到各种球对应的概率。根据题意,每个人摸两个球,关键是“无放回”,即第一次摸到的球,第二次不会再摸到,再根据获得的礼金券计算平均收益即可。
解:根据题意画出树状图,如下:
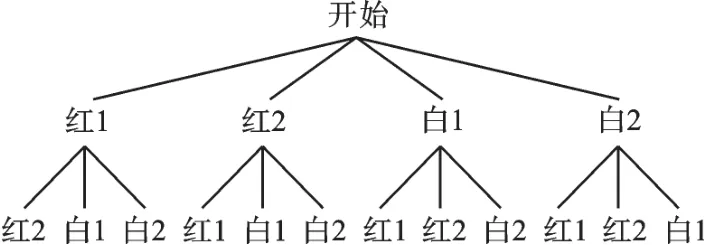
由图可知,P(两红)=,
P(两白)=,
P(一红一白)。
所以我会选择去甲超市购物,因为在甲超市获得礼金券的平均收益多。
解决概率问题时,我们要从概率的意义出发,理解等可能性事件。画树状图或列表前更要读懂题意,抓关键词,从而巧妙地解决问题。

