改进遗传算法的汽车悬置系统多目标优化设计

雷芳华 潘洁宗

（1.郴州职业技术学院；2.上汽通用五菱汽车股份有限公司）

为改善汽车的舒适性，提高整车的减振（NVH）水平，在汽车动力总成悬置系统多目标设计的过程中，振动优化设计一般优化悬置位置、刚度等参数，以系统的固有频率和解耦程度为合理设计目标，把惯性参数作为已知参数[1]，又由于解耦优化目标函数和设计参数的多目标复杂性，同时也存在多个局部最优解，从而需要寻找一个合适的算法去搜索到全局最优解。一般的优化算法，如牛顿法、梯度法、遗传算法等容易陷入局部最优解。在遗传算法（GA）算子的改进方面，文献[2]提出利用个体之间的海明距离、文献[3]提出利用不同的交叉策略、文献[4]提出利用动态调节交叉、变异概率的方法来克服早熟问题，并且加强了局部搜索能力，大大提高了遗传算法的全局寻优能力。因此，文章提出了一种改进选择算子的方法，通过染色体不同的适应度设置调节因子，从而形成动态染色体复制概率，保持染色体的多样性，避免了遗传算法过早收敛的问题，通过算例对比，达到了预期的效果。

1 悬置系统数学模型

一般情况下，都是把动力总成视为刚体，同时把动力总成悬置系统视为具有3 个移动自由度和3 个转动自由度的空间6 自由度振动系统，对应6 个模态，包括前后移动模态、左右移动模态、上下移动模态、横向转动模态、纵向转动模态和左右转动模态。悬置系统数学模型，如图1 所示。

图1 汽车动力总成悬置系统六自由度数学模型图

在动力总成上建立1 个动坐标系G0-XYZ，原点G0位于动力总成质心，系统动力模型通过3 个具有三向弹性（阻尼）的元器件支承，在悬置系统中，阻尼能有效地减少系统的振动，由于阻尼对于固有频率和解耦程度的影响较小，一般可以忽略不计。根据上述动力总成悬置系统力学模型建立6 自由度无阻尼自由振动方程，如式（1）所示。惯性矩阵（M），如式（2）所示。刚度矩阵（K），如式（3）所示。

式中：q——动力总成（刚体）在广义坐标系下的坐标x，y，z 及绕 x，y，z 轴的转角 θx，θy，θz的总和；

m——动力总成的质量，kg；

Jx，Jy，Jz——动力总成分别绕x，y，z 坐标轴的转动惯量，kg·m2；

Jxy，Jyz，Jxz——动力总成对应下标平面的惯性积，kg·m2；

K——3 个悬置点减振元器件在x，y，z 向刚度值的总和，K=k1，k2，…，k9，N/m；

Ei——第i 个悬置点坐标位置组成的矩阵，m；

Bi——第i 个悬置点的安装方向角余弦值组成的矩阵，（°）；

Di——第i 个悬置点的x，y，z 向刚度矩阵，N/m。

目前应用比较普遍的模态解耦度评价指标是用模态的能量比值概念来表示的，也就是对于一个频率，单个模态能量与总模态能量的比值表明这个模态能量的强弱。第j 阶振型中第h 个自由度的振动能量占该阶运动总能量的百分比，如式（4）所示。

式中：dighj——第j 阶振型中第h 个自由度的振动能量占该阶运动总能量的百分比，%；

φj——第j 阶振型向量；

eh——第h 个元素为1 的6 阶单位列向量。

在一个频率下，一个模态能量占总能量的98%就表明这个模态能量非常强，在实际工程中，一般情况是难以达到这种解耦度的。一般如果在某个频率下，一个模态的能量占85%以上，那么这个模态与其他模态的解耦程度则被视为满意，对于横向转动模态要求更高，期望达到90%以上[5]282。

2 悬置系统多目标优化设计

2.1 适应度函数

悬置系统优化设计采用模态的能量比值作为目标函数。悬置系统特性受多种因素影响，比如动力总成的惯性参数和悬置系统的安装位置、角度以及刚度值等，由于惯性参数和系统位置、角度受到车架和其他器件的空间限制，也难以进行改变和调整。因此文章将以 3 点悬置的 9 个刚度值 K=（k1，k2，…，k9）作为设计变量，以6 个自由度的最大解耦度为优化目标函数，采用统一目标法将多目标优化问题转化为单目标优化问题进行求解。因此，适应度函数经过加权组合后的关系式，如式（5）所示。

式中：F——染色体i 的适应度；

w1，w2，…，w6——各自由度相对应的权值，且w1+w2+…+w6=1；

digi——各自由度上的最大解耦，i=1，2，…，6。

2.2 约束条件

在实际隔振优化中，需要通过悬置系统6 自由度完全解耦或者部分解耦及合理配置固有频率，才能最终实现减小振动耦合。在合理配置固有频率方面，为了保证系统的使用寿命，系统6 个固有频率都要大于5 Hz[6]，动力总成作为激励力，系统固有频率小于激励力频率时，才能使得隔振效果最佳[5]283。文章中选择的发动机怠速转速为800 r/min，为保证隔振效果最佳，计算系统固有频率应小于18.6 Hz，因此该悬置系统的固有频率（fi/Hz）应该满足 5 Hz≤fi≤18 Hz（i=1，2，…，6）。从某种程度来说，为避免悬置系统产生内部共振，系统各阶模态之间的最小固有频率差值应该大于1 Hz，然而人最敏感的频率范围为4～6 Hz。综上，悬置系统的固有频率最好能控制在 6 Hz≤fi≤18 Hz（i=1，2，…，6）。那么，通过有效地控制悬置系统的固有频率，进一步地优化刚度设计变量。然而，刚度过低容易导致过大的静变形，刚度过高又会不利于减振，因此，要求悬置刚度约束满足设置要求，如式（6）所示。

为了便于算法的简洁操作和高效运算，刚度的设计变量约束范围将设置为算法初始种群的随机输入范围，而固有频率约束将设置为一个检测固有频率的子程序，实现约束检测功能。

2.3 改进遗传算法的算子选择

2.3.1 算子选择

GA 中选择算子就是从当前种群中根据每个个体的适应度值按概率选出优良的个体，使它们有机会作为父代为下一代繁殖子孙。个体的适应度越高，被选择复制的机会越多，也就是繁殖的机会越多；反之，机会就越少，甚至被淘汰。为了进行动态的选择复制操作，需要对种群中的每个个体设定一个复制概率，则第i 个染色体被复制的概率，如式（7）所示。

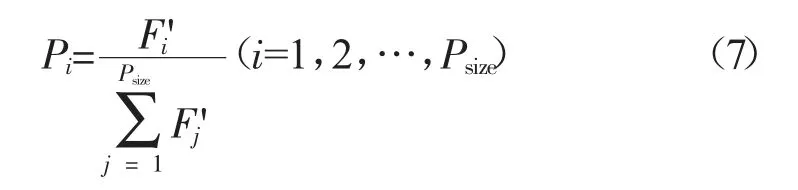
式中：Pi——第i 个染色体的复制概率（i=1，2，…，Psize）；

Psize——种群设置的总数；

引入一个控制染色体多样性的调节因子，则动态定标适应度关系，如式（8）所示。

式中：GEN——遗传算法的遗传代数，一般取GEN=100，200，…，600；

r——遗传到第r 代；

δ——控制染色体多样性的调节因子，δ 一般取10，20，…，60。

2.3.2 遗传操作

按照遗传算法的操作，计算适应度值，运用轮盘赌选择法复制，再对种群染色体进行交叉和变异等遗传操作。文章中确定种群大小Psize=30，最大遗传代数GEN=400，其中交叉因子（Pc）和变异因子（Pm）为预定值，其值越大，能保持的多样性就越好，越能防止早熟。因此，为了测试改进后选择算子的作用，设置较小的预定值，取 Pc=0.3，Pm=0.2。

3 优化算例

针对某国产自动挡车型的振动问题，分析其动力总成悬置系统的隔振效果，为了便于动态分析，首先设置参考悬置系统的基本理论参数。表1 示出动力总成的质量和惯性参数。表2 示出悬置系统位置和优化前的刚度参数。

表1 某车型悬置系统惯性参数表

表2 某车型悬置系统位置和优化前的刚度参数表

表3 某车型悬置系统优化前各阶频率及能量分布表

根据传统遗传算法和改进遗传算法进行方案优化，表4 示出经过传统遗传算法和改进遗传算法优化后的悬置刚度参数。表5 及表6 分别示出传统及改进算法优化后的各阶固有频率及能量分布。从表5 及表6中可以看出：传统遗传算法优化后，θx，θz方向上的解耦度已经让人较满意，但是X，Z，θy方向上的解耦度却还是一样，与其他方向的耦合程度还是很高；改进遗传算法优化后，几乎所有方向上的解耦度都可达到99%，解耦结果让人较为满意。

表4 某车型悬置系统传统及改进算法优化后刚度参数对比表N/m

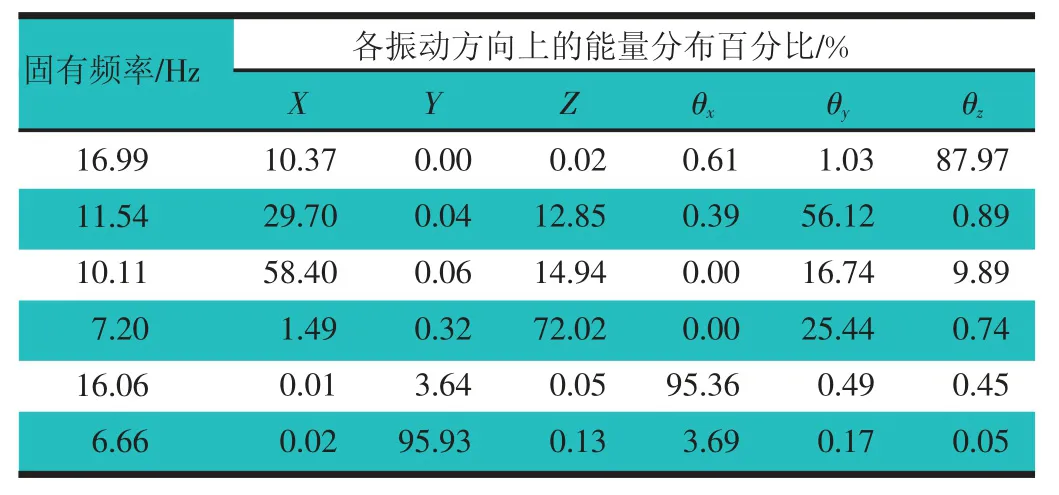
表5 某车型悬置系统传统遗传算法优化后各阶频率及能量分布表

表6 某车型悬置系统改进遗传算法优化后各阶频率及能量分布表

在优化过程中，染色体多样性的动态分布情况能直接决定遗传算法全局搜索能否寻找到最优解，避免出现早熟现象。表7 示出2 种遗传算法的优化性能对比。从表7 中可以看出，2 种算法的初始适应度值是处于优化的同一起跑线的，但是由于传统遗传算法的染色体多样性控制能力较差，使得适应度值进化到第10代的时候，F=0.800 2，基本趋于平稳，优化的效率低，而且优化结果不令人满意。

表7 2 种遗传算法的优化性能对比表

然而改进遗传算法的适应度值在进化到第100 代时，F=0.999 5，基本也趋于平稳，由于优化初期尽可能地保持了染色体的多样性，使得收敛结果让人较为满意。

4 结论

文章改进了GA 算法中的选择算子，设置了动态定标适应度，从当前种群中根据每个个体的适应度值按概率选出优良的个体，个体的适应度越高，被选择复制的机会越多，繁殖的机会越多；反之，机会就越小，甚至被淘汰。经过优化算例的计算结果表明，该算法将各自由度的解耦度提高到99%，适应度提高到0.99，在实际优化工程中很好地控制了染色体的多样性，防止了早熟现象，能高效地应用于动力总成悬置系统的多目标优化设计，大大地提高了悬置系统多目标优化设计的可靠性。该优化的刚度参数是否可行，将在后续企业配置动力总成悬置系统减振元器件中得以验证。