无机晶体材料热膨胀系数理论计算及实验研究

王于静 赵 静 陈 稳 杨 军

(陆军工程大学 1通信工程学院， 2基础部，江苏 南京 211101)

热膨胀系数是材料在工程应用中的关键参数，如在结构材料和功能材料等领域有广泛应用[1-4]。目前主要是通过实验测量获得，然而实际材料的种类繁多，考虑到实验设备性能、经济成本及材料本身的限制，热膨胀系数不能完全依靠实验测得，有必要建立一种理论计算方法来快捷有效地获得材料热膨胀系数。晶体材料热膨胀系数的理论计算可以分为经验晶体化学方法[5-9]和理论计算方法[6,9]两大类型。经验晶体化学方法考虑到热膨胀是材料所固有的属性，由组成晶体的化学成分和晶体结构所决定的，该方法以实验测量数据为基础，结合材料化学成分、化学键、离子价态、配位数以及电子结构等参数，建立其与热膨胀系数之间定量关系的方法。但经验晶体化学方法有一定的局限性，目前仅能给出晶体材料平均热膨胀系数，而且只能针对简单晶体结构的晶体更有效。此外，经验晶体化学方法也不适合计算某一特定温度下热膨胀系数，因此需要发展更普适的有温度依赖关系的热膨胀系数计算理论和方法。

1 理论计算方法

根据固体理论，如果只考虑原子间简谐振动，则势能曲线左右对称，平均值为零，并不能引起晶体的膨胀，所以晶体膨胀是原子间非简谐振动的结果。如果考虑到势能的高次非谐项，则原子运动方程不是线性微分方程，且原子状态的通解不再是特解的线性叠加。为此，A.R.Ruffa[7-11]从量子理论出发，建立了用于热膨胀计算的定量计算Ruffa模型。Ruffa 模型中通过引入Morse势来表达原子间的相互作用势，一方面考虑到Morse势求解薛定谔方程具有明确的解析解，另一方面，相对于量子谐振子模型，Morse势能够更好的描述非谐效应。对于离子晶体化合物，Morse势可以表达为[8,12]

(1)

上式中，a,D和r0分别表示势垒宽度倒数、势垒深度和能量最低点平衡位置。对于式(1)，从物理上理解,方程右边第一项对应排斥势函数，第二项则为吸引势函数。根据量子力学理论，Morse振动能En和平均原子间距〈rn〉则可以表达为[8]

(4)

(5)

(6)

(7)

(8)

热膨胀系数α1(T)对温度T的依赖关系则可以表达为(8)式对T微分[12]：

(9)

其中，

(10)

方程(10)称为Debye函数，考虑方程(3)忽略的高次项，则热膨胀系数的修正项为[8,12,13]

因此，包括修正项的总热膨胀系数可以表示为

α(T)=α1(T)+α2(T)

(13)

2 焦绿石结构晶体热膨胀系数理论计算

2.1 理论计算

图1 La2Zr2O7焦绿石晶体结构图(晶体学空间群227)

为验证上述晶体材料热膨胀理论的正确性，我们以焦绿石结构的陶瓷材料La2Zr2O7为例(晶体结构如图1所示)，结合式(2)～(13)进行理论计算并与实验测量结果进行对比。根据上述分析，如果要计算晶体材料的热膨胀系数，必须先得到rn，D，a以及θD等参数。需要指出的是上述理论方法是适合二元化合物，对于多元化合物则需要将其参数描述为相应的二元化合物参数的线性组合。例如，La2Zr2O7的平均原子间距可以利用加权平均来确定原子间距：

(14)

式中，rLa，rZr和rO分别为La离子的有效半径(配位数为8)；Zr离子的有效半径(配位数为6)以及O离子的有效半径(配位数为4)，相关参数如表1所示，经过计算La2Zr2O7平均原子间距237pm。

表1 焦绿石晶体结构La2Zr2O7各元素的离子半径

对于D的计算，考虑到采用复杂的势能函数并不能提高计算精度，为此Ruffa采用包含吸引和排斥势的相对简单且物理意义明确的Born势：

(15)

(16)

对于Born势能和Morse势能之间的关系，Ruffa采用下列经验方程：

其中，Debye温度θD可以利用实验测量值，也可用下面的关系式进行估算(对有些材料估算值与实验值有一定偏差,可以直接采用实验值)：

(19)

对于斥力因子m, Ruffa提出如下经验公式[7-11]：

(20)

其中，q为平均电价，采用晶体的原子价的最大公约数;mq为多价化合物的斥力因子;m为对应阴阳离子配位相同的单价化合物的斥力因子。计算表明，Ruffa因子估算方法对于卤化物非常有效，其理论计算值与实验测量值符合较好，但对于氧化物需要进一步修正，为此Inaba给出了以下公式[10,11]：

(21)

其中，mo为氧化物的斥力因子;ma为对应卤化物的斥力因子;mr为Ruffa斥力因子;c是一个取决于元素周期表的周期和氧化物中金属元素存在的d层或f层电子的系数.需要指出的是上面的计算方法仅适合计算二元化合物的热膨胀系数，对于La2Zr2O7计算则相关参数需要将相应的参数进行线性组合[14]。

2.2 实验测量

本文采用固相反应法制备测试样品，工艺流程简述如下：将所需的原材料氧化物粉末于800～1000℃煅烧1h，后根据要求按一定化学计量比混合，用无水乙醇作为混合介质，氧化锆为球磨介质球磨混料，转速为250～300rpm。球磨后对浆料进行旋转蒸发，然后置于120℃干燥箱干燥12h，过400目筛，在适当的温度下煅烧成预成相粉体。将固相法制备的陶瓷粉体采用压片机20MPa保压5min压制初始素坯，成型坯体经220MPa冷等静压2min后于干燥箱中放置24h，用于释放静压过程中产生的内应力。将制备的坯体在空气中采用无压烧结，烧结相关温度参数为室温至1000℃，升温速率为5℃/min，高温段1000℃至1600℃升温速率为3℃/min，烧结温度为1600℃，保温10h。降温速率为5℃/min，得到高致密陶瓷多晶样品，样品的扫描电子显微镜(Scanning Electron Microscope，SEM) 微观形貌如图2所示，从图中可看出样品致密度高，晶粒发育良好，晶界清晰，无第二相出现。该结论可以进一步从X射线衍射(X-ray diffraction, XRD)图谱(图3)中得到证实，从图3中可以看出，样品的X射线衍射峰尖锐，晶化完全，特别是(331)和(511)特征衍射峰表明其为有序焦绿石结构(空间对称群227)。随后根据测试仪器要求对样品尺寸进行加工，并完成平整度加工和表明抛光处理。

图2 La2Zr2O7 多晶陶瓷SEM表面形貌图

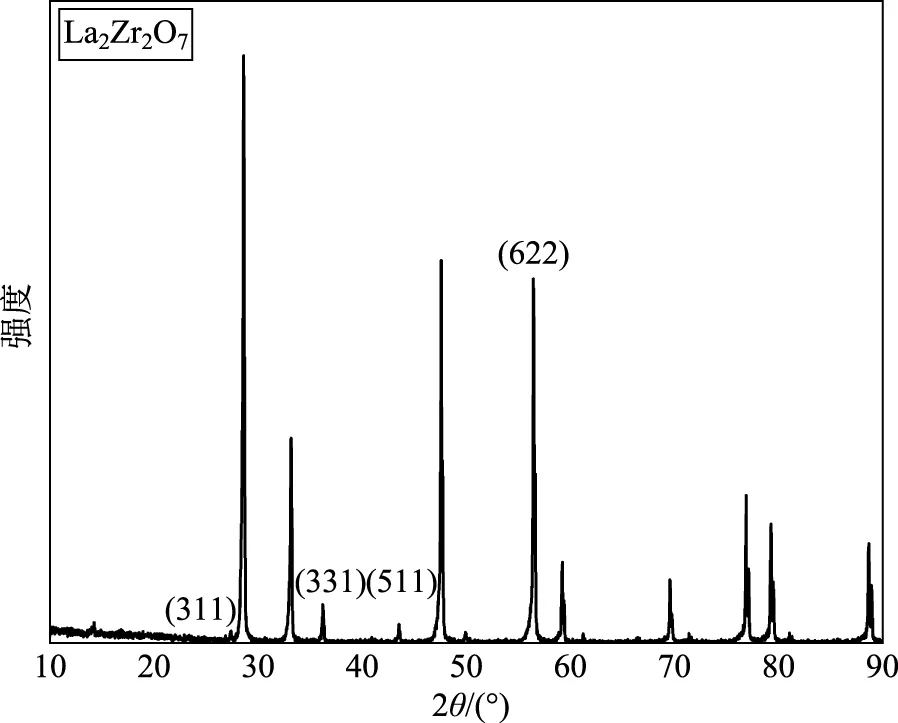
图3 La2Zr2O7 XRD衍射图谱

本文中采用推杆法热膨胀仪(NETZSCH，德国，DIL 402PC)测量样品热膨胀系数，具体原理为采用高精度位移计测量样品在升温过程中的长度变化，从而计算出热膨胀系数。测试前要多次测试氧化铝标样，得到准确基线后再对待测样品进行测量，测试温度范围为室温到1500℃，升温速度为50℃ /min，测试气氛为空气。测试过程中要保持测试设备的高度稳定性，避免振动。

2.3 结果及讨论

La2Zr2O7晶体热膨胀系数理论计算及实验结果如图4所示，可以看出，理论计算结果与实验测量结果总体趋势符合得较好，特别是在高温阶段，理论计算和实验测量误差很小，表明理论模型的合理性和有效性。在低温阶段，理论计算值要高于实验测量值，主要源自于两个方面，一是低温阶段实际材料的原子振动非谐性比理论模型低，导致实验值低于理论模型预测值。二是实际测量材料为多晶材料，其对热膨胀系数的宏观值有一定影响。需要指出的是，高温热缺陷对其热膨胀系数有很大影响, 而Ruffa 模型没有考虑其影响, 致使高温下实验值和计算值也存一定的偏差[6]。尽管如此，从图4中可以看出，理论预测与实验测量值整体符合得较好，验证了理论模型计算的准确性和实用性。为此，我们利用该方法计算了系列的氧化物热膨胀系数，如图5所示，分别计算了不同稀土离子半径的稀土锆酸盐氧化物： Sm2Zr2O7，Gd2Zr2O7， Yb2Zr2O7及多元氧化物 Sm2FeTaO7的热膨胀系数，可以看出，稀土锆酸盐氧化物在低温阶段热膨胀系数随温度的上升变化较快，但在高温段趋向于恒定值，这与杜隆-柏替定律要求相一致。

图4 La2Zr2O7 热膨胀系数理论计算及实验值

图5 多元氧化物热膨胀系数理论计算(a) Sm2Zr2O7； (b) Gd2Zr2O7； (c) Yb2Zr2O7； (d) Sm2FeTaO7

3 结语

考虑到晶体材料的多样性和复杂性，实验测量晶体材料存在一定的局限性，本文介绍和发展了一种预测无机晶体材料热膨胀系数的一种有效方法，并通过固相反应法实验制备了高质量的焦绿石结构的La2Zr2O7晶体材料进行试验测量对比。研究表明，理论模型计算和实验测量符合得较好，验证了理论模型的有效性和准确性，为快速预测无机晶体材料的热膨胀系数提供了一种有效的方法。