数形结合在小学数学解题中的应用
梁桂春

【摘要】在小学数学教学中,培养学生的解题能力是重要的教学目标,解题能力也是数学核心素养的重要组成部分.小学生的思维是以形象思维为主,引导他们用数形结合的方式,能够有效地提升他们的解题能力.基于此背景,对数形结合在小学数学解题中的应用策略进行了探究,希望能够达到一定的借鉴意义.
【关键词】数形结合;数学解题
对数形结合而言,就是在数学中实现数量关系和空间形式的有机融合,这是一种典型的数学思维方法.通过数形结合的方式,可以有效地简化数学问题,能够借助图形的方式使学生获得更直观、更形象的感知,同时也能够在条件问题以及答案之间成功地架构桥梁.针对小学数学问题而展开的解决教学实践中,依托于数据结合的方式,能够有助于优化问题的解决过程,进而提升其数学核心素养.
一、借助数形结合,降低问题难度
“形”最突出的特点就是直观,就小学生而言,仍以直观形象为主要思维方式,小学生面对抽象思维以及数学解题,大都会受制于思维难度,不但运用较少,甚至还会出现无从下手的局面.引导学生运用数形结合的方式就能够有效地降低数学问题的难度.
例如,在教学“替换以及鸡兔同笼问题”的过程中,可以给学生设计这样一道题:笼中的鸡和兔子一共有8只,腿合计22条,那么请问鸡和兔各有多少只?针对这一问题的解决,借助数据结合的方式便可以有效降低问题的难度.教学过程中,教师可以引导学生通过画图示的方式进行解决.
这样,学生通过画图就可以很快地得出鸡有5只,兔有3只,并且,在画图的过程中,能够把假设的数学思想进行具体化.
在小学的中低段,具体的教学过程更多的是激发学生的学习兴趣,实际上针对抽象思维以及数形结合等相关知识的教学,教师也应善于利用这一特点,或者链接学生生活,或者选择更直观的图文结合方式,这样学生就可以联系自己的经验实现对问题的自主解决,既有助于发展其数学思维,也有助于促进其数学探究.
二、借助数形结合,找准关键条件
对小学生而言,实际解决问题的过程中,必须准确把握问题的条件,否则就会在解决问题的过程中失去方向.教师应引导学生依托于数学问题的语言,并以此为基础进行图像演示,这样就能够成功地将抽象化的数学语言转化为直观的图形,必然可以准确把握问题的关键条件,明晰具体的解题思路.
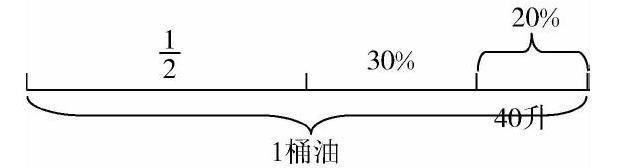
例如,一桶油漆经历了两次使用之后余下还有40升,第一次用去了整桶的12,第二次用去的是整桶的30%,请问这桶油漆总共多少升?针对这道分数应用题的解答,首先需要学生准确把握题目中的已知条件,并了解条件之间的关联,这样才能够明确具体的解题方向.所以此题的解题关键在于余下的40升所对应的分数,也就是其在整桶油漆容量中的实际占比.如果依靠字面理解的方式,很容易引发学生思维的混乱.由此可以在审题的过程中,借助画线段图的方式,先分别标示出第一次、第二次使用量的占比以及余下的40升.学生在画图的过程中会以整条线段表示整桶油漆(具体的单位为1),之后在线段中分别标示出两次使用量的占比,这样就可以直观地感受到余下的40升在整桶油漆中的实际占比为20%.
结合线段图的方式,实现了对抽象问题的简单化以及形象化处理,有助于学生快速准确地把握解题突破口,顺利实现对这一问题的有效解决.
三、借助數形结合,明确解题思路
学习数学并非为了应试,是为了掌握一种基本的生活技能,同时也是对文化的传承.学习数学最主要的功能就是生活中的应用,比如,算账、理财,这些都是比较常见的数学知识运用的实例.所以在小学数学教学实践中,应用题往往更贴近生活,也是数形结合应用最普遍的一个方面.
华罗庚曾经提出过这样的观点:人们很早就对数学这门学科形成了枯燥乏味的刻板印象,导致这一现象的关键原因在于脱离实际.对数形结合而言,既是理论和实践的有机融合,同时也是一种更有效的方法和手段,可以帮助小学生完成基本数学模型的架构.通过数形结合的思想,有助于集中直观的图形以及抽象的数字,既实现了互补,也实现了二者的有机结合,同时还使得问题更立体、更形象,可以帮助学生准确把握要件,明确解题思路,有助于促进多方位思维能力的发展.
例如,行程问题:小明、小红两家相距12千米,二人约好同时前往图书馆,小红以步行的方式,每小时行走4千米,小明选择骑自行车,每小时的速度是小红的3倍.小明追上小红需要多久?
针对此题的分析,很多学生会感到混乱,由此便可以借助数形结合的方式,引导学生画出线段图就能够帮助学生准确把握要件,迅速完成对问题的解答.
在小学数学应用题中,追及问题是其中极为重要的知识板块,具有多样的题型,难度也有所不同.针对此类问题的解决,首先应当具备良好的逻辑思维能力.但是在题目中会涉及较为复杂的信息量,很容易引发学生的混淆,如果借助线段图的方式,既直观又形象,同时也可以标示出关键的信息,这样学生便能够轻松实现解题.数形结合的思想,能够更直观地体现数与形各自不同的特点,同时也能够突出二者之间的联系,是一种非常有效的解决问题的方式.
总之,在解决问题的数学实践中,依托于数学结合的思想,既有助于促进小学生的数学思维,同时也能够更有效地激发他们主动探究的兴趣.所以,教师应有意识地渗透数学结合的数学思想,同时也应当在实践中为其搭建促进试炼的平台,这样才能够帮助学生积累更丰富的经验,才有助于数学素养的全面提升.

