小学六年级数学错例分析及教学对策研究

陈赛姬

六年级学生在数学学习上的错误是多种多样的，错误的原因也五花八门。本文结合相关文献的研究和与六年级学生的访谈结果，将六年级学生数学典型错例划分为几类后进行具体的错因分析，并给出相应的教学对策。

一、知识性错误

知识性错误是指学生对概念理解不清、运算定律的使用不当、知识记忆不牢。它主要表现在学生对数学知识认识上的缺陷。

1.概念理解不清

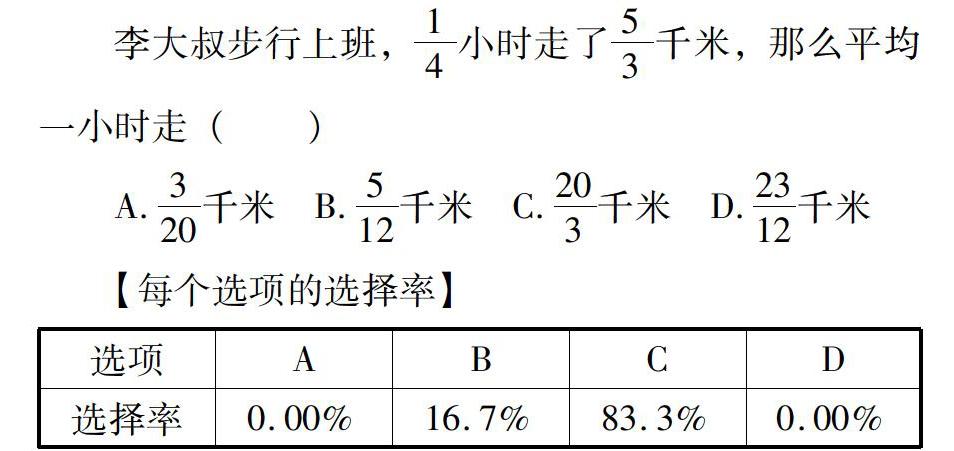
数学概念是数学教学的重要组成部分，正确地理解概念，是学生学好数学的前提和保障，也有利于学生正确地解答实际问题。概念理解不清主要是指学生对概念的理解不到位，不能识别出题目所涉及的概念，导致不会应用正确的数量关系解决问题。

【错因分析】对速度的概念理解不到位，不知道求平均一小时走的路程实际上就是求李大叔的速度;不清楚题目数据的含义，如1/4小时表示时间，5/3km表示1/4小时走的路程，要求的是李大叔的速度，速度=路程÷时间。

【教学对策】1.加强对速度概念的分析，让学生默读概念，把概念的关键点圈出来，再举例说明。2.重视对学生读题习惯的培养，要求学生一边读题，一边把题目的已知条件用横线画出来，并写上已知是时间、速度、路程还是单价、总价、数量等，再把题目的问题用波浪线画出来，并写上要解答的是时间、速度、路程还是单价、总价、数量等，根据要解答的量是什么，找到解决问题对应的数量关系式。

2.运算定律的使用不当

六年级的乘法分配律的学习，是在四、五年级整数乘法分配律、小数乘法分配律学习的基础上，推广到的分数乘法。由于乘法分配律的运用比较灵活，学生没真正理解乘法分配律的本质，导致运算定律使用不当。

【错误率】36.6%

【错因分析】乘法分配律掌握不好，不懂得把括号外面的4×5看成一个整体，分配给括号里面的每一个数。

【教学对策】1.首先，让学生按四则运算的顺序算出正确的结果，与此题的结果作比较，从而产生疑惑，为什么两种方法算出来的结果会不一样呢。其次，出示题目（100-7）×4×5○100×4×5-7×4×5，问学生，左边表示几个4×5，学生很快能得到93个4×5，右边表示的是几个4×5减几个4×5，学生也很快能得到是100个4×5减掉7个4×5等于93个4×5，从而明白，应该把括号外面的4×5看成一个整体，分配给括号里面的每一个数。2.类型题巩固训练。

3.知识记忆不牢

德国心理学家艾宾浩斯研究发现，学生对于理解了的知识的记忆，比不理解的知识的记忆要容易得多。在六年级分数乘法的教学中，我们经常会遇到学生因为不理解分数乘法的意义，只是机械地记忆计算法则，知识记忆不牢导致出错;在已知体积，反过来求出高、底面积等时，学生只是机械的记忆公式，不知道公式是怎样推导出来的，这是知识记忆不牢导致的。

【典型错例】

一辆货车箱是一个长方体，它的长是4m，宽是1.5m，高是4m，装满一车煤，将这车煤堆成一个高是2m的圆锥形，它的底面积是多少平方米？

错解：4×1.5×424÷2=12（m2）

=6×4

=24（m3）

错误率：20.5%

【错因分析】1.学生不知道圆锥形煤堆的体积就是长方体车厢的体积。2.圆锥的底面积公式记错。

【教学对策】1.用捏泥让学生理解圆锥形煤堆的体积就是长方体车厢的体积。2.让学生经历圆锥底面积、高的公式推导过程。

二、策略性错误

小学六年级学生解题的策略有：①借助画图、列表等手段分析题目;②找出题目的关键句，利用关键句构建解题模型。策略性的错误一般有表象加工整理技巧欠缺和解题模型构建能力差。

1.表象加工整理技巧欠缺

画图便于分析题意，有的题目，图画出来了，结果也就出来了;有的题，图画好了，题意学生也就明白了。但是画图依赖于人们对表象加工整理的可靠性，学生表象加工整理技巧欠缺，不会借助画图、列表等手段去分析题目，导致出错。

【典型错例】

把一个直径10厘米圆分成两个相等的半圆，两个半圆的周长和是（）

A.31.4

B.51.4

C.41.4

D.62.8

【每个选项的选择率】

【错因分析】从与学生的访谈，可以看出学生在没画图之前，对两个半圆的周长和并不清晰，也不习惯借助画图的方法去分析题意。

【教学对策】1.注重对学生画图分析题意能力和习惯的培养。画图能使抽象的数学问题变得形象化，直观化，有助于提高学生解决数学问题的能力。但在我们的教学实践中，经常可以看到学生不会或者不愿意借助画图去分析题意，因此，教师应该从低年级开始就鼓励学生用自己喜欢的方式来画图，激发学生的画图分析题意的兴趣，并通过展示学生的创意作品等来增强学生的自信心，体验画图策略带来的便捷及成就感，同时教师也要加强对学生画图分析题意方面的指导，实现学生愿意用画图策略，会用画图策略。2.加强类型题和对比题型的练习。比如把题目的直径为10厘米改为半径为10厘米，其他条件不变;或者把题目改为，把周长为25.7厘米的半圆拼成一个圆，这个圆的周长是多少？

2.解题模型构建能力差

找出题目的关键句，根据关键句写出等量关系式，建立正确的解题模型，是我们解决分数百分数应用题的一般步骤，学生解题模型构建能力差，一般是指学生未能利用关键句写出正确的等量关系式，或者未能利用数形结合，建立起正确的等量关系式。

【典型错例】

汉阳村有个种粮大户，前年收稻谷26000千克，去年比前年增产了三成，这个种粮大户去年手里多少稻谷？

错解1：26000×30%=7800（千克）

错解2：26000÷（1+30%）=20000（千克）

【错因分析】1.学生不懂得借助线段图去分析题意。2.不理解去年比前年增产三成的意思。3.不懂把关键句去年比前年增产了三成转化成等量关系式前年收到稻谷×（1+30%）=去年收的稻谷。

【教学对策】1.让学生读完题，找出题目的关键句，分析关键句讲的是什么与什么作比较，比较的结果怎样，画线段图表示，根据线段图得出等量关系式，把关系式中已知的量写在它下面，未知的量打个问号在等量关系式相应的量下面，再根据已知跟未知的量，确定是用乘法还是除法计算。2.类型题对比题强化训练。

三、心理因素造成的错误

学生在解题的过程中，一般都要经过读题识别，找出题目中的问题和条件，利用记忆中储备的知识分析解决问题所需要的条件，选择恰当的条件进行解题，再回顾反思。可見，学生能否正确解题，除了跟他所掌握的知识技能、解题策略有关系，还跟他解题时的心理因素息息相关。比如，解题时一味追求做题的速度，急于求成导致错误;看到数据能凑整，没去分析题目含有什么运算，盲目“凑整”导致错误。

综上所述，六年级学生错例的产生，有些源自于学生对概念的理解不清、运算定律使用不当、知识记忆不牢等知识性错误，有些源自于学生表象加工整理技巧欠缺、解题模型构建能力差等策略性错误，还有些源自于学生急于求成、“凑整”心态等心理因素造成的错误。在教学过程中，我们要夯实基础，注重知识的形成，要加强解题策略的训练，还要了解学生的解题心理。

【本文系广州市天河区教学科学规划课题“基于单元测试数据提升小学数学错例分析及教学对策能力的策略研究”研究成果之一】

责任编辑 罗峰