动能定理在物理问题教学中的应用——以空气阻力上抛运动为例

刘万海，王 翔

(1.绵阳师范学院数理学院，四川绵阳 621006；2 .兰州城市学院，甘肃兰州 741000)

0 引言

学生在物理课程的学习中，对物理规律的理解、掌握和应用是非常重要的教学内容和任务.空气阻力[1-6]的上抛运动问题在中学物理中主要作为中学教师的自我提升，对中学生没有作过多要求，而且初入大学的学生由于在高中阶段几乎没有深入学习微积分知识，因此大学生对物理规律进行深入的理解、掌握和应用有一定的困难.本文响应目前教育部倡导的高校“金课”建设的要求，并且针对大学生的以上学习困难，利用大学生掌握的基本微积分知识，在大学物理教学中积极引导学生讨论与实际生活紧密相关的物理问题，以培养学生对物理规律更好地理解、掌握和应用.

1 问题描述

在考虑空气阻力的情况下，物体从抛出点上升到最高点时所用时间(上升时间)t上和该物体从最高点落回到原位时所用时间(落回时间)t下的大小关系，以及上升(落回)距离H上(H下=H上)与上抛(落回)速率v上(v下)之间的关系.

我们知道，不考虑空气阻力时的上抛运动是中学物理教学过程中的教学重点内容之一.在不考虑空气阻力的情况下，做竖直上抛运动的物体到达最高点之后开始下落直到抛出点为止.关于其上升和下降阶段所用时间之间的关系等问题，可以从不同的角度进行讨论.从运动学知识可知，上抛阶段可视为匀减速直线运动，而下落阶段视为匀加速直线运动.两个阶段物体的加速度方向均为向下，大小相等，即重力加速度. 因此，上升阶段物体运动的距离以及所用时间和下落阶段物体运动的距离及所用时间分别相同.在相同加速度的情况下，进而可以得知抛出速度的大小和落回原处时的速度大小也相同.从机械能的角度来说，只在重力作用下的运动物体而言，其机械能守恒.也就是说，运动物体经过上抛运动之后又回到原处时，其重力势能没有变化.因此，其动能一定保持不变，从而得出落回原处时速度大小和抛出时的速度大小相同.从动量定理来看，上升阶段和下降阶段物体动量的变化量大小相同，从而重力的冲量大小也相同.因此，两阶段物体所用时间相同.总之，对于不考虑空气阻力时的抛体运动，我们可以运用的研究途径很多.

然而，现实生活中的运动物体难免要受到空气阻力的作用.空气阻力的存在，给我们研究抛体运动带来了不小的挑战.空气阻力不像重力那样总保持竖直向下，而总是和物体运动方向相反.同时，空气对运动物体阻力的大小也不像重力那样只与物体的质量有关，而是跟运动物体的形状、体积大小和运动快慢有关.其中，物体的形状因其外形的不同而千变万化，目前为止还无法对物体的形状给予定量描述.为此，空气阻力和运动物体之间的定量关系很难确定.空气阻力，指空气对运动物体的阻碍力，是运动物体受到空气的弹力而产生的.物体在运行时，由于前面的空气被压缩，两侧表面与空气的摩擦，以及尾部后面的空间成为部分真空，这些作用共同所引起的阻碍作用.在逆风运行时，还要把风力附加在内.在现实生活中，自由落体也受空气阻力的影响，其速度、接触面积和空气密度等都会影响空气阻力的大小.通常，我们通过实验的方法，对特定形状的运动物体在一定情况下所受的空气阻力的大小进行研究.在理论研究中，我们通常采用一定的物理模型来处理空气阻力的存在.

已有文献[7]对考虑空气阻力的上抛运动，运用牛顿第二定律和泰勒公式展开法进行了详细讨论，给出了上升时间小于落回时间的结论.本文从动能定理出发，对该问题进行了较为深入的讨论，本着通过一题多解、举一反三和触类旁通的方式对动能定理更加深入地理解，使学生达到熟练掌握和应用的目的.

2 动能定理应用分析

以下对该问题首先进行定性分析，然后进行定量计算与讨论.

2.1 定性分析

(1)

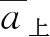
(2)

考虑关系式(1)，容易得出

t上

(3)

说明在空气阻力作用下，上升时间t上小于落回时间t下.

2.1.2 用动能定理讨论上抛速率和落回速率之间的大小关系 根据动能定理：

(4)

将初、末位置选在抛出点、落回点(两点重合)，上式(4)变为

(5)

v上>v下，

(6)

说明在空气阻力作用下，上抛速率v上大于落回速率v下.

2.2 定量计算

在空气阻力作用下，物体在上升阶段所受合力为mg+f上，与运动方向相反做减速运动，下降阶段所受合力为mg-f下，与运动方向相同做加速运动.为了研究方便，将上升阶段等价为从最高点到抛出点之间的加速运动.这样，我们只需要研究从最高点到下落距离H的两种加速运动.这两种运动中物体所受合力为F=mg+bf，其中b=1和-1分别对应上升和下降过程.因此，对于初速度为0，下落H时速率为V的运动过程，依据动能定理，有

(7)

其中重力mg为常量，对其积分后得到

(8)

(9)

这样，当空气阻力的表达形式已知时，关于抛出点速率的关系式就得到了.为了讨论方便，我们取空气阻力的表达式为f=βvα，其中α可取0和1.当α=0时，β=f0，空气阻力为恒力的情况；当α=1时，β=k(常系数)，空气阻力与速度成正比的情况.下面分别进行讨论.

2.3 讨论

(1)α=0时，上式(9)积分后得到

(10)

从而得到

(11)

(12)

(2)α=1时，将其带入积分式(9)后，得到

(13)

δ=bξ-ln(1+bξ).

(14)

因此，我们可以得到上升(取参数b=1)和下降(b=-1)阶段距离随速度的变化关系分别为

δ上=ξ上-ln(1+ξ上),

(15)

δ下=-ξ下-ln(1-ξ下).

(16)

我们将无量纲距离随无量纲速率的变化关系作图1.

图1 无量纲距离随无量纲速率的变化关系Fig.1 The Relationship between Dimensionless Distance and Dimensionless Rate

图1中虚线表示加速下降阶段落回距离随落回速率之间的变化关系，实线也表示加速运动过程中距离和速率之间的关系，但其对应的是减速上升阶段，即该曲线表示的是上升距离和上抛速率之间的关系.从图1中曲线可以看出：在考虑正比于运动速率的空气阻力时，无论在上抛阶段，还是在下降阶段，上抛速率或落回速率越大，物体的上升距离或落回距离越大.如取相同的上抛或落回速率ξ=0.4时，上升距离不超过0.075，而下降距离超过了0.10，其差别较大.在上升距离(落回距离)一定时，我们看到上抛速率大于落回原位时的速率：如δ≈0.11时，上抛速率超过了0.5，而落回速率仅为0.4，其差别较大.

通过上述讨论可知，在考虑空气阻力的情况下，利用匀变速直线运动规律定性得出了上升时间小于落回时间的结论。利用动能定理定性判定了上抛速率大于落回速率，进而通过定量计算，证明了定性分析所得结果的正确性，同时给出了上升距离(落回距离)和上抛速率(落回速率)之间的定量关系式.总之，空气阻力对上抛运动有很大的影响.当然，当物体的运动速度较大时，空气阻力和速率的关系较为复杂，这里不做介绍.

3 结语

本文在考虑空气阻力的情况下，应用匀变速直线运动的相关规律和动能定理对上抛运动进行了定性和定理分析，很好地体现了物理规律在实际物理问题教学中的应用.其实，由于空气阻力的存在，我们日常生活中遇到的很多物理现象，如平抛运动、斜抛运动、上抛运动、弹簧谐振运动和单摆的摆动等，都可以借助相应的物理规律进行深入研究.而且，目前的很多软件，如数学软件Mathematica、Maple、Matlab，绘图软件Tecplot、Origin等，能为我们进行科学研究提供很好的辅助作用，起到事半功倍的效果.讨论这类实际问题，可以加深我们对物理规律的理解和掌握，同时，也可以更好地研究实际生活中的物理现象，解决真实情景下的物理问题.因此，在大学物理教学中，物理教师要多提出类似的物理问题，鼓励学生积极参与讨论和研究，从而提高学生分析问题和解决问题的能力.