融合GMS与VCS+GC-RANSAC的图像配准算法

丁 辉，李丽宏*，原 钢

（1. 太原理工大学电气与动力工程学院，太原030000； 2. 中国煤炭科工集团太原研究院，太原030000）

（∗通信作者电子邮箱ya721@163.com）

0 引言

图像拼接和图像配准是图像处理中十分重要的部分。其中图像配准是图像拼接的基础，也是图像拼接最重要的一个环节。图像配准在医疗卫生［1］、机器人［2］、自动驾驶［3］、人脸识别［4］、图像检索［5］、目标跟踪等领域都有广泛的应用。图像配准大致可分为灰度分析和基于特征分析两种方法［6-7］。灰度分析主要是一类特定模板对目标图像基于灰度评价函数的滑动匹配，受光照、角度和尺度变换影响较大；而基于特征分析的配准方法由于对光照等鲁棒性较好，现已成为该领域主流的分析方法。

基于特征的图像配准分析方法大致可分为三个步骤:特征点提取、特征点匹配、计算空间变换模型。对于特征点提取算法，有经典的尺度不变特征转换（Scale-Invariant Feature Transform，SIFT）［8］，还有在其基础上基于速度和精度方面的优化；在提取速度优化方面有SURF（Speeded Up Robust Features）［9］、ORB（Oriented FAST and Rotated BRIEF）［10］、AKAZE（Accelerated-KAZE）［11］等算法；在提取精度优化方面有PCA-SIFT（Principal Component Analysis-SIFT）［12］、ASIFT（Affine-SIFT）［13］等。特征点描述子粗匹配通常采用暴力匹配原则（Brute-Force）与快速最近邻搜索库（Fast Library for Approximate Nearest Neighbors，FLANN）［14］；而在特征点精匹配步骤中，普遍使用随机抽样一致性（RANDom SAmple Consensus，RANSAC）算法［15］进行错误点剔除。但当样本数据繁多且模型外干扰点数量大时，算法局部最优模型收敛时间会呈指数型增长；同时剔除后也会存在一些明显的错误匹配点。为了兼顾配准速度和精度，Bian 等［16］提出一种基于网格运动统计（Grid-based Motion Statistics，GMS）的算法，该算法利用网格将粗匹配点区域化，统计各小区域中匹配关系的特征点数量，以此进行错误匹配剔除。该算法运行速度能达到实时效果，缺点是会有明显的匹配错误没有剔除。朱成德等［17］提出一种通过根据左右图匹配对距离相近原理改进的RANSAC 算法，算法原理简单易懂，运行速度快；但该算法通过一个距离范围进行错误点剔除，当配准图像是大视角旋转缩放时，正确匹配对也会有极大的距离，这种情况下算法会把大量正确匹配点进行剔除，故对于有缩放和旋转的图像配准效果并不好。Barath 等［18］提出图割随机抽样一致性（Graph-Cut RANSAC，GC-RANSAC）算法，该算法通过在RANSAC 的局部优化环节利用图割算法（能量函数）区分内野点，优化效果和全局最优模型都极佳，缺点就是当野点较多时，算法的运行速度受到极大限制。

针对以上各算法缺陷，本文提出一种融合GMS 与VCS+GC-RANSAC 图像配准算法:首先通过ORB 对图像进行特征点提取并对特征点进行暴力匹配；之后通过GMS 算法对图像做网格划分，利用网格中正确匹配点具有一定的特征支持量原理对粗匹配对进行第一次剔除；接着利用图像特征点与正确匹配点构成的向量可由指定向量相加而成，应用矢量系数相似性（Vector Coefficient Similarity，VCS）原理对匹配对进行进一步剔除、整理，减小错误匹配所占比例，以利于后面算法减少迭代次数与运行时间；最后利用GC-RANSAC 算法建立局部最优模型，得到高精度配准图像。

1 网格运动统计

网格运动统计（GMS）算法［16］是一种基于匹配对邻域特征点支持量的评价方法。它主要是对经过ORB 特征提取以及暴力粗匹配后的特征匹配进行过滤。图1为GMS邻域特征点支持量原理示意图。以图1 为例，正确匹配对邻域内有两个正确匹配支持量，而错误匹配对邻域内没有正确匹配对对其支持。具体算法原理如下:假定标准图和待匹配图分别为Ia、Ib，其上有两个已匹配完成的粗匹配区域Ra、Rb。假定Ra中含有n 个特征点集合｛a1，a2，…，an｝，Rb中含有相对应的n 个特征点集合｛b1，b2，…，bn｝。Ra、Rb区域的n 个匹配对集合为｛x1，x2，…，xn｝，其中xi=(ai，bi)表示一对特征点匹配对。设Si为xi匹配正确时，其邻域Ra中特征点支持量，则

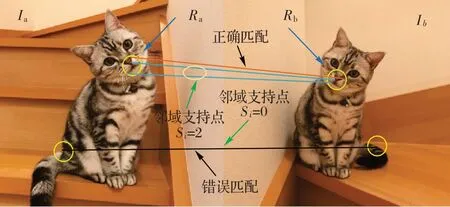
图1 GMS邻域特征点支持量原理示意图Fig. 1 Schematic diagram of GMS neighborhood feature point support principle

由式（5）可知，当Ra、Rb匹配错误时，Ra中一个特征点恰好还匹配到Rb区域的一个特征点几率近乎为0，至此便证明错误特征匹配对邻域内近乎没有特征匹配对支持的理论。

由式（3）、（4）可知，特征匹配邻域内特征点支持量符合二项分布，即:

为了提高匹配速度，将标准图与配准图像网格化；同时，为了将正确匹配时特征点支持量与错误匹配时特征点支持量差距拉大，统计目标网格及其周围8 个网格的特征点支持量作为目标网格区域某一特征匹配的支持量。因此，邻域特征点支持量变为:

其中:K 代表与所在网格区域相邻不相交的网格数。由式（7）可得Si标准差与均值:

根据Si的标准差与均值设定区分正确与错误匹配邻域特征点支持量阈值:

在实验中发现mf通常极小，而Sf较大，同时α较大可以有极高的置信度拒绝大量错误匹配对，所以mf可以忽略，即:

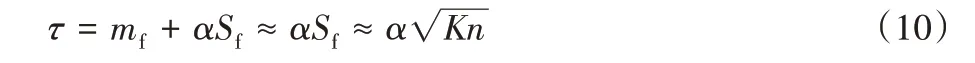
对于一个网格区分正确与错误匹配邻域特征点支持量阈值

其中:na表示9个网格中特征总数的平均值。

通过式（11），将待配准网格中粗匹配对邻域特征点支持量大于τi保留，将小于τi的粗匹配点剔除，即完成了GMS算法对粗匹配对的筛选。

图2 匹配过程中各事件的相互关系Fig.2 Relationship between events in matching process

2 VCS+GC-RANSAC

2.1 图割随机抽样一致性

图割随机抽样一致性（GC-RANSAC）［18］于2018 年被提出，旨在克服一些传统RANSAC算法不足。通过实验和仿真，其在一系列问题上（直线拟合、仿射矩阵、基本矩阵的估计）的结果比传统RANSAC算法更加精确。

传统RANSAC主要算法步骤为:

1）随机挑选计算模型所需最小点数子集；

2）计算模型相关参数；

3）计算所建立模型与所有点的距离，根据距离阈值将点集内点分为内点与野点；

4）保存内点个数和模型对应的基础矩阵；

5）重复以上步骤，迭代k次得到k个模型及其对应的内点与基础矩阵；

6）通过评价函数比较k个模型，最后输出最好模型。

GC-RANSAC 主要对传统RANSAC 算法的步骤3）（局部最优）进行优化改进，传统RANSAC算法对于模型内点和野点的区分仅仅依靠一个阈值，没有考虑数据的空间结构。传统RANSAC根据式（12）区分内野点:

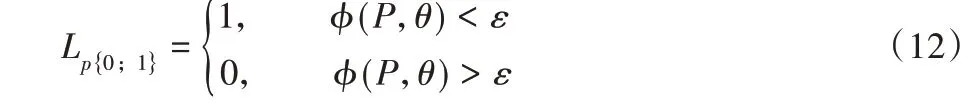
其中:P 为点集中一点；θ代表模型；φ 为距离函数；ε 代表点距模型距离的阈值。

GC-RANSAC 算法提出运用一元能量函数对内野点区分进行改进:

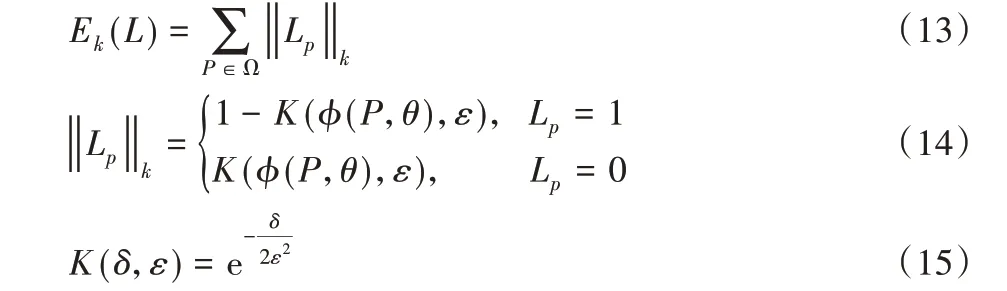
式（13）中:一元能量函数Ek(L)表示对点集Ω中单个点P与模型距离进行惩罚。由式（14）、（15）可知，当标签为1（内点）距离模型越近惩罚越小，当标签为0（野点）距离模型越近惩罚力度越大。将所有点惩罚值相加便得到一元能量函数。

当数据包含很多野点，且这些野点与模型距离也比较近，在这种情况下，对不同标记的邻近点使用相同惩罚会导致野点的主导优势，这样会使所有内点被标记为野点。针对这一问题，GC-RANSAC算法通过考虑点与点之间的空间结构一致性，提出基于空间一致性的能量函数Es(L):

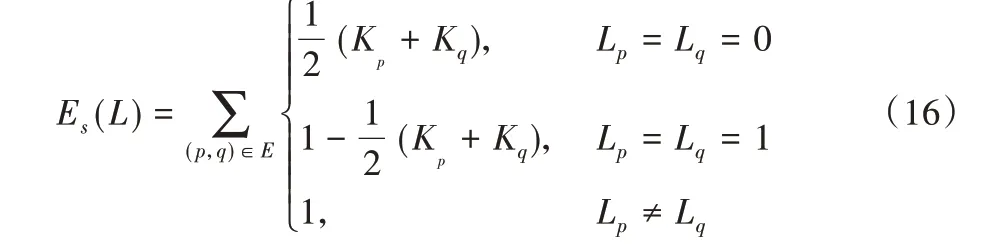
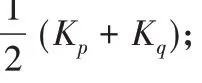
将两个能量函数结合成一个多项式，该多项式既考虑点对模型的匹配度又考虑空间结构一致性，即

其中:λ是一个平衡参数。

全局最佳标记L*= min E(L)，利用图割算法可计算得到E(L)的最小值时点集标记。

2.2 VCS+GC-RANSAC原理

尽管GC-RANSAC 较之前RANSAC 和LO-RANSAC 算法，大幅提高了精度，但当野点（在图像配准中即为错误匹配点）比例占点集数量（匹配集）较大时，算法可能会迭代很多次才能找到局部最优模型，这样算法的运行速度和效率就会受到极大影响。

在图像配准中，即使图像经过缩放、旋转、平移，但其各个特征点与特定的稳定特征点之间位置相对关系并不会有很大改变（稳定特征点与各个特征点构成一个整体），即由基向量运算得到的特征点矢量系数不会有太大的突变。

由此本文提出一种基于矢量系数相似性（VCS）原理对错误匹配特征点进行部分剔除的方法。以下为原理详解。

根据平面向量基本原理提出假设:任一平面内任一向量均可以由两不共线的向量相加得到，经基本仿射变换后，该向量表示形式不变。

由式（20）可得:

将式（18）代入式（21），可得

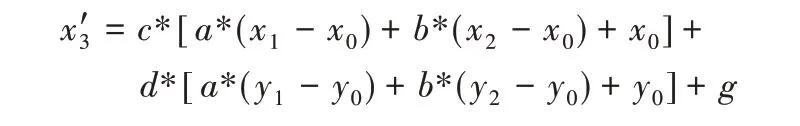
合并其他项整理得:

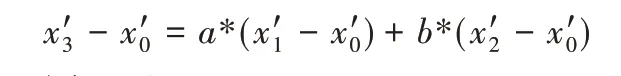
同理可证:

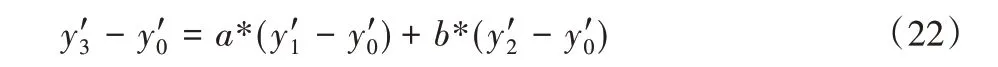
对比式（19）、（22）可证向量经仿射变换后由两向量相加的系数不变性。考虑到一些客观问题，本文算法将通过一个系数相似性阈值进行错误匹配剔除。

综上，基于VCS的GC-RANSAC算法步骤如下:

1）挑选3 组稳定、正确且不共线的匹配对，将匹配图与待匹配图的3个特征点组成两特征基向量；

2）将待评价的匹配对分别与稳定匹配对之一组成向量，并求得它们在特征基向量下的系数值；

3）将对应的系数值做相似度对比，判断相似度值是否大于给定相似阈值T，符合条件的匹配对即组成样本集S；

4）将样本集S作为GC-RANSAC 算法待检测样本，求出局部最优模型。

3 实验与结果分析

为了验证本文所提改进算法运行速度与匹配精度的优异性，将本文算法与SIFT+RANSAC、ASIFT+RANSAC、GMS+GCRANSAC、AKAZE+RANSAC、GMS 进行比较，测试平台为个人笔记本:其中操作系统Windows 7，Intel core i5-4210M CPU@2.6 GHz 内存为4 GB，算法通过Visual Studio 2015 编译平台编写C++代码进行实现，测试数据集为Oxford 标准仿射变换图集及现实拍摄图集。

采用匹配正确率（Correct Matching Rate，CMR）［20］与匹配时间两个指标对算法进行综合评价，其中CMR 评价指标的定义为:

其中:nc为特征点对匹配正确的数目；nt为算法得到的总的匹配对数目。nc可由Oxford 图集所提供的仿射变换矩阵真值获得。

图3 展现了本文算法与SIFT+RANSAC、AKAZE+RANSAC、GMS 算法在Oxford 图集的6 个子数据集的CMR 对比。实验序号1～5 是各个算法在测试数据集序号2～6 的图像与标准图1 配准结果。数据集中包含了光照明暗对比（Leuven），视角尺度对比（Wall、Graf、Boat）以及模糊度对比（Trees、Bikes）三类配准测试图像。由图3（a）、（b）可以看出本文算法在处理模糊配准方面相较于其他三种算法更加稳定，匹配精度平均可达92%以上；四种算法在光照强度对比方面（图3（f））匹配准确率相差不多，但本文算法仍具有些许优势。在视角尺度变化方面（图3（c）～（e））可以看出所有算法在实验5 匹配精度近乎为0，这是因为视角变换太大时，匹配难度呈指数型增长，而本文算法也因GMS 算法所提邻域特征点支持量急剧下降，导致正确匹配率骤跌。但本文算法相较于其他三种算法在前4 次实验仍有较大优势。而且本文算法相较于文献［17］算法在视角尺度方面（图3（c）实验5 以及图3（e）实验4）也具有一定优势，这主要是由于GC-RANSAC 相比RANSAC有更强的局部最优模型的刻画。

图3 不同算法在Oxford数据集上的CMR实验Fig.3 CMR experiment for different algorithms on Oxford dataset

为了展示本文算法与其他算法的不同，下面将对算法综合指标进行评价。图4（b）～（f）展示了以Oxford 图集中bark子数据集实验5 为例（原图为图4（a）），应用本文算法与ASIFT+RANSAC、AKAZE+RANSAC、GMS、GMS+GC-RANSAC 算法进行图像配准的结果。Bark子数据集是Oxford数据集中配准难度最大的数据集，包含了极大角度的视角转变和尺寸缩放，这对配准提出了极大挑战，表1 是本文算法在Bark 子数据集实验的量化展现。由图4配准图可以看出，ASIFT等算法较本文算法有更多特征匹配对，但本文算法匹配对平顺且无明显的错误匹配对，ASIFT 算法虽然有很多特征对匹配出现，但匹配杂乱无章，有许多可见错误匹配对。AKAZE+RANSAC 与GMS 匹配虽然较本文算法运行速度较快，但在配准图示中可以清晰可见有错误匹配对。GMS+GC-RANSAC算法匹配图也有可见的错误匹配对。遵循配准中正确率首要的准则，虽配准数量较少但匹配平顺且无明显的错误匹配对的本文算法，相对于其他4个算法具有一定优势。

表1 不同算法在Bark数据集实验5的运行结果比较Tab. 1 Comparison of running results of different algorithms in Bark dataset experiment 5

图4 Bark数据集上实验5原图及不同算法的配准结果Fig.4 Original image and registration results of different algorithms of experiment 5 in Bark dataset

通过表1 各算法表现分析在全局表现中，本文算法在平均匹配精度上提高了30.34%，平均匹配时间缩短了0.54 s。在局部对比方面，本文算法虽然比ASIFT 算法最后得到的匹配对数量少，但匹配正确率比ASIFT 高3.465 个百分点，且运行时间几乎仅是ASIFT 的一半，这对实时性要求高的情况是非常重要的。本文算法较AKAZE、GMS 的运行时间分别多了0.734 s、0.503 s，这是由于GC-RANSAC 算法比RANSAC 寻找局内最优模型需要更多时间，而且GMS 的算法邻域特征点支持量也需要比其他暴力匹配算法需要更多的时间；但匹配精度比两种算法分别提高了62.12%、52.03%。这种在大视角变换情况下的配准正确率提高是十分重要的，是求取配准图与待配准图之间的仿射变换矩阵真值，进行真实图像拼接的十分重要一步。本文算法由于在GC-RANSAC 之前对样本进行了一次筛选，故而比GMS+GC-RANSAC 拟合最优模型迭代次数更少，运行时间更短，同时正确率也有提高。综上所述，考虑配准确率及运行时间两个评价指标，本文算法优于其他4种算法。

为进一步展示本文算法的实用性，对现实所拍实物图集进行配准，该图集包含了煤矿巷道所用液压支架的大角度视角变换和重复性纹理物体在暗光严峻条件的大角度视角变换。从如图5 所示的配准效果中可以看出，配准平顺无明显错误对，本文算法在实用性方面有很好表现。

图5 本文算法在现实所拍数据集上的配准效果Fig.5 Registration results of the proposed algorithm on real dataset

4 结语

本文针对现有配准算法在复杂环境中配准正确率较低、配准时间较长的问题，提出融合GMS 与VCS+GC-RANSAC 的配准算法，经权威数据集以及现实所拍图集的测试对比与验证，说明了本文算法的鲁棒性和高效性均有提高。但算法在大角度视角转变环境下的一些配准仍存在欠缺，改进本文算法以期在复杂视角下的配准取得更好效果是下一步研究的方向。