基于邻域信息的改进模糊c均值脑MRI分割

王 燕，何宏科

（兰州理工大学计算机与通信学院，兰州730050）

（∗通信作者电子邮箱hk_smile@qq.com）

0 引言

图像分割就是根据人们的需要将图像分为若干个具有相同性质区域的过程［1］，分割后的区域具有区域内属性相似度高、区域间相似度低等的特点。磁共振影像（Magnetic Resonance Image，MRI）是应用放射性磁场将人体的各种组织描绘成图像的过程。脑MRI 图像主要由灰质（Grey Matter，GM）、白质（White Matter，WM）和脑脊液（Cerebrospinal Fluid Rhinorrhea，CSF）三大组织组成［2］，而MRI 技术是区分这些组织和结构必要手段，对于研究解剖结构的变化和脑量化是必不可少的途径。同时，这三大组织也是模拟肿瘤生长的先决条件，肿瘤根据周围组织以不同的速度扩散。由于MRI 技术简单方便，经常被用于脑功能、脑部病变的诊断和研究。而脑MRI 图像因为其在形状上的复杂性和多样性，现有的文献中出现了许多方法应用MRI 技术来检查身体的异常情况，如分水岭技术、多级阈值技术、聚类技术和边缘检测技术等方法。

聚类是一种运用生物信息学的自动分割技术，在图像中应用普遍，很多人对此进行了研究与应用。聚类可分为k 均值和c 均值两大类。模糊c 均值（Fuzzy c-Means，FCM）聚类是最普遍的。它的原理是依照不同的标准将数据进行分类，按照均方逼近的理论，使目标函数达到最小，迭代计算出合乎设定阈值的聚类中心和隶属度，而后依照计算出的聚类中心和隶属度矩阵来对数据分类。该算法遵循模糊集理论［3］，具有实现容易、花费时间少等优点；同时具有容易受到初始中心的影响、目标函数陷入局部极值、对噪声敏感等缺点［4］，导致分割后图像并不令人满意。

近年来，研究人员提出很多利用FCM 算法来分割脑图像的方法。文献［5］在目标函数中引进犹豫度优化聚类，提出了直觉FCM（Intuitionistic FCM，IFCM）聚类算法，十分适合于医学图像分割，但该算法对犹豫度的定义不够清晰。文献［6］将改进的遗传算法与FCM 相结合，在彩色图像中的分割结果很好，但未涉及医学图像分割。文献［7］引入了FCM_S 算法，经过在目标函数中增加像素的灰度信息，分割效果较好，是一种很好的方法，但是计算量比较大。文献［8］提出了一种直觉无中心的FCM（Intuitionistic Center-Free FCM，ICFFCM）聚类算法，用直觉模糊隶属函数来定义像素到聚类的相似性，很好地解决了脑MRI 图像的模糊性和聚类过程中的不确定性；抗噪性较好，但运行时间长。文献［9］将像素的局部空间信息与灰度信息相结合，提出了一种抗噪声性强的聚类算法——模糊局部信息c 均值（Fuzzy Local Information c-Means，FLICM）算法；但该算法对图像的分割精度不高。文献［10］提出了一种自适应正则化的基于内核的FCM（Adaptively Regularized Kernel-based FCM，ARKFCM）算法，用高斯径向基核函数替换了FCM 聚类中的欧氏距离，以较低的计算成本达到更高的分割精度。但是算法抗噪性不高，对噪声很大的图像进行分割时容易造成图像缺失。

本文结合像素的邻域提出了改进的FCM 图像分割方法。首先，通过计算马尔可夫随机场的最大化条件概率来表示周围像素对该像素的影响。然后，将其引进到FCM 算法的目标函数中，在目标函数中增添修正项，改变目标函数的计算公式，改善算法的抗噪性。因为普通的FCM 算法易受初始值的影响，容易造成算法的不稳定性或部分图像的缺失，因此，采取文献［14］中提出的自适应遗传算法对数据进行全局优化，确定初始聚类中心，从而提高分割的效率和精度。经过对比实验验证，该方法在对脑MRI 图像进行分割时拥有更好的分割精度和抗噪性，同时耗费时间比较少，提升了现有FCM 算法的效率。

1 本文改进的FCM算法

1.1 马尔可夫随机场表示的邻域信息

图像分割领域中的马尔可夫随机场理论经常用于图像处理技术中，常用此体现像素与像素间的关系。由于在图像的像素划分中，马尔可夫随机场使用了像素的邻域信息，因此具有很强的抗噪性。在马尔可夫随机场模型中，像素的类别由像素的邻域决定，马尔可夫模型假设图像具有马尔可夫性，设有一像素点xik，则以像素xik为中心选择一邻域范围ηik。那么定义在该像素点后的马尔可夫模型为X=｛Cxik|Cxik∈｛1，2，…，C｝｝，Cxik是像素xik的类别标号［11］，C为类别数，被判别为第c类的概率是Pci。如图1 所示，像素xik的邻域为ηik=｛t1，t2，…，t8｝，依据哈默斯利-克利福德定理可以得出，马尔可夫随机场等价于Gibbs 随机场，由此可得马尔可夫的空间信息服从吉布斯分布（联合概率分布），计算公式如下:

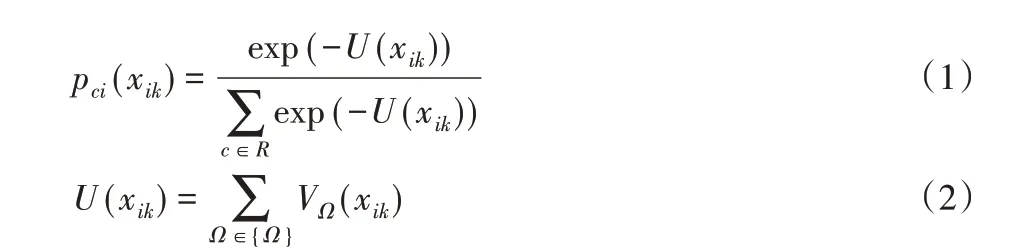
依据式（2），等式左边代表的是能量函数，右边代表的是势团Ω 的势团函数，Ω 是所有势团组成的集合。在马尔可夫模型的图像中，像素点的标记受周围像素的影响，像素越远受影响越小。为了提升计算效率，采取迭代条件模型，即整幅图像在其标号域中的条件概率等于对应标号域中各点的条件概率密度的乘积。最后，利用极大似然法确定模型参数，通过最大化条件概率更新像素标签。

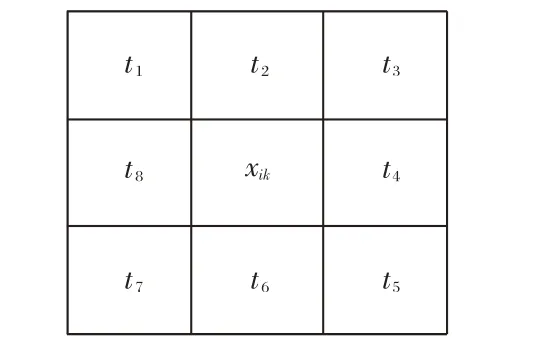
图1 xik的邻域ηikFig. 1 Neighborhood ηik of xik

1.2 改进的FCM图像分割算法

FCM 算法是利用目标函数来解决图像分割问题，经过求目标函数的最小数，迭代出隶属度矩阵和初始值，依据隶属度矩阵和聚类中心对数据进行划分，从而实现对图像的分割。假设有一图像像素集合X=｛xk|k=1，2，…，n｝，n 代表图像中像素点的个数，c 为聚类数。改进的FCM 算法利用在目标函数中加入马尔可夫模型表示的像素邻域，来改变隶属度矩阵的求解方法，从而提高算法的抗噪性能。因为马尔可夫随机场模型在图像分割时联系了像素的邻域信息，因此具有良好的抗噪性能，从而提高了算法的抗噪性能。在目标函数中加一正则项引入马尔可夫随机场表示的邻域信息，即用马尔可夫的最大化条件概率代替隶属度矩阵，改变后的FCM 算法目标函数的表达式为:

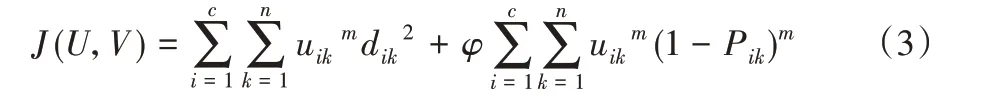
其中:uik为第k个像素对于第i类的从属程度；dik表示第k个像素到第i 个聚类的标准的欧氏距离；Pik是用马尔可夫随机场代表的像素xik的空间邻域信息；φ 是约束系数，用来调整目标函数的约束能力。依照拉格朗日乘数法计算出隶属度矩阵和聚类中心的新计算式。新的表达式为:

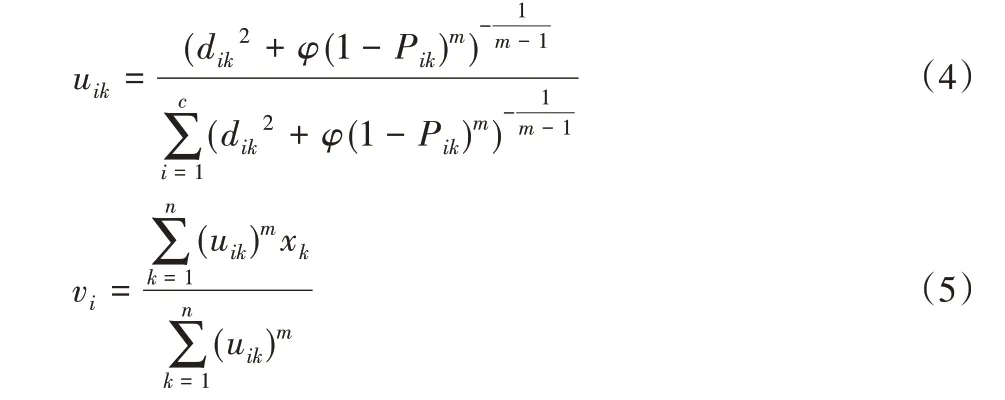
其中:vi=｛v1，v2，…，vc｝是c个初始的聚类中心；m∈［1，∞）为模糊指数，用来控制数据分类的模糊度［12］。在m=1 时，聚类是硬c均值聚类。Nikhil 等［13］研究发现m 的最优取值范围为［1.5，2.5］，通常m=2是比较理想的取值。

当算法收敛到一定阈值时，终止迭代，依照隶属度矩阵和初始中心划分数据，最后更新图像的像素值，输出分割后的图像。

2 算法实现过程

2.1 自适应遗传算法确定聚类中心

由于聚类算法对初始中心的敏感，因而不适当的初始值会使得聚类的结果较差并造成图像的缺失。在传统的FCM算法中，初始中心是随机选定的，并且随机的初始聚类中心可能会使数据离某些聚类太远，从而增加了算法的迭代次数。

为了防止随机初始值对分割效果的影响，采取文献［14］中的自适应遗传算法来优化初始值。因为遗传算法能够在全局内对数据寻优，是一种寻找最优解的方法，能够提高算法的稳定性。自适应遗传算法［14-16］主要组成如下:

Step1 初始化参数。每一个个体由c*s 的浮点数表示，其中c是聚类数，s是数据维度。

Step2 生成初始的种群。实验中随机选择3个样本作为一类，取均值作为初始值共c 次。种群的大小一般在30～75，实验种群数为50。

Step3 计算适应度。为使得染色体的质量更高，利用适应度来评估染色体的质量。适应度一般选用优化后的FCM算法的目标函数（式（3））的倒数，计算公式如下:

Step4 计算遗传算子。

1）选择:依照生物进化论原则，采取非线性排序选择方式，按适应度降序排序，按相应的编号计算非线性选择概率。

2）交叉:计算交叉概率，增大种群的稳定性。

3）变异:计算突变概率，防止交叉形成局部收敛，增加种群的多样性。

Step5 设置运行参数。为了保证结果最优，参数设置为:交叉概率0.6，变异概率0.1，最大迭代次数100，收敛精度为0.000 01。

Step6 解码输出聚类中心V（0）。

2.2 改进的FCM算法流程

改进的FCM算法流程如图2所示。

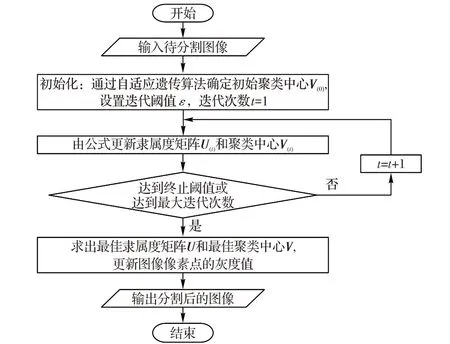
图2 改进的FCM算法的流程Fig. 2 Flowchart of improved FCM algorithm

首先输入待分割图像，由自适应遗传算法确定初始的值V（0），再依据式（4）～（5）计算隶属度矩阵和聚类中心；当达到设定的阈值abs（Jt（U，V）-Jt-1（U，V））＜ɛ 或最大终止次数时，终止算法的迭代；然后，依据各类别的聚类中心和隶属度矩阵进行像素的划分，依据隶属度的最大值将图像的像素划分类别；最后，更新像素的灰度值，并输出分割后的图像。

3 实验与结果分析

实验中所用的数据集选用McGill 大学Montreal 神经所的Brain Web 脑MRI 图像库［17］。该数据库仿真了脑MRI 图像的各种组织和结构，包含了基于两种解剖模型（正常和多发硬化）的脑MRI 数据，并且提供了三种合成方式（T1-，T2-，PD-）下的三维脑MRI 图像。图库中含有不同的扫描厚度、噪声和灰度灰度不均匀的大脑图像。每组图像数据的大小为181×217× 181，图像像素值取值范围为［0，255］，数据库提供了全部脑MRI 图像的金标准图像，按照这些图像能够比较算法划分的准确性。

脑图像主要由GM、WM、CSF组成。这三大组织是最为重要的组成部分，是脑肿瘤等疾病生长的前提，更加准确地分割出上述部分拥有很重要的实际意义。因此在实验之前，为了更加准确地进行分割，事先剔除了脑图像的其他部分，切片厚度为1 mm，取聚类数目c=4（即GM、WM、CSF和背景），模糊指数m = 2，迭代阈值ε=0.000 01，最大迭代次数T=100。图像像素邻域为3× 3 邻域，实验环境为Matlab2018a。在实验中，将本文算法与FCM 算法、FLICM 算法、ARKFCM 算法进行了对比。

通过经验得出当约束系数φ=0.6 时，实验获得的分割结果图像较好。

3.1 检测抗噪性实验

为了检测算法的抗噪性能，在实验中选择BrainWeb 图像库作为实验数据库，并以T1 加权，选取脑切片图像第100 个MRI 图像为例。图3（a）是包含所有组织的原始大脑MRI 图像，图3（b）～（d）是去除了大脑其他组织后的图像，依次显示了不同噪声的图像。

图3 实验使用的图像Fig.3 Images used in the experiment

对图3（d）的图像依照4 类分割来检验该方法的可靠性。表1 为FCM 分割过程当中随机选取的聚类中心、用自适应遗传算法确定的聚类中心和聚类后的聚类中心。从表1 可以看出:随机选取的方式就是随意取用c 个像素作为初始值，在某种程度上增加了算法的不可控性，具有一定的随机性。采用自适应遗传算法确定初始的聚类中心更加接近于聚类后的聚类中心，验证了该方法的有效性，提高了算法的效率。

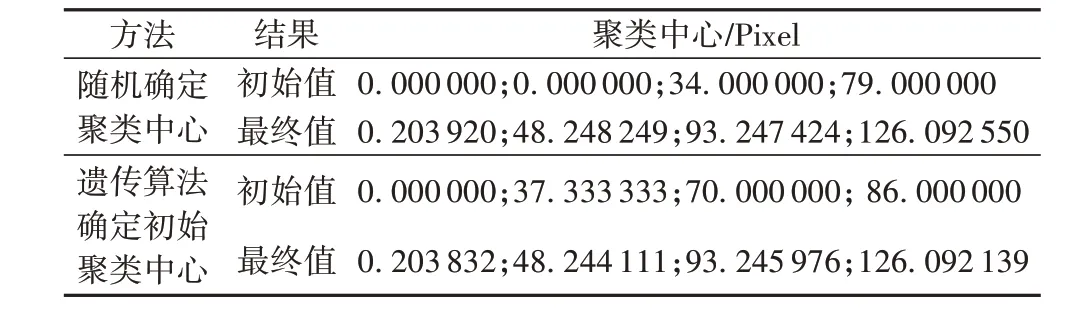
表1 MRI图像FCM分割实验聚类中心Tab. 1 Clustering centers of MRI image in FCM segmentation experiment

从图4所示的实验结果可看出:1）本文的PSNR 值高于对比算法，即抗噪效果较好，其他算法的实验效果不明显。经典的FCM 算法易受初始值的搅扰，需要进行多次实验才能得到想要的分割图像。2）FCM算法没有很清楚地分割出脑脊液与脑灰质图像，脑脊液与脑灰质交织在一起，抗噪性差。如实验中对于在7%的噪声与40%的灰度不均匀图像的分割中，ARKFCM 算法对于白质的分割中含有噪声，没有完全分割出白质，造成了图像的缺失。整体来看，本文的算法的抗噪性优于对比算法，具备较好的抗噪性能，实验效果较好。

在对实验结果的评价中，实验效果的好坏容易受到个人情感因素的干扰。为更加准确地评价算法的抗噪强弱，实验中选用峰值信噪比（Peak Signal-to-Noise Ratio，PSNR）来评估算法的抗噪性，并对FCM、FLICM、ARKFCM 与本文算法进行比较和说明。PSNR是一种基于灵敏度的评价指标，用于客观评价算法的抗噪性，它基于对应像素点间的误差，并不受个人情感因素的影响［18］。PSNR的表达式如下所示:

表2 不同算法的图像峰值信噪比对比 单位：dBTab. 2 Comparison of PSNR for different algorithms unit:dB

其中:MSE 为均方误差（Mean Square Error）。PSNR 能够很好地评估算法的抗噪声能力，表示的是分割后图像与原图的像素之间的误分率，数值越大，说明分割后的图像质量越高，算法的抗噪性越好，像素的误分越小。实验后获得的图像如图4 所示，分别代表了实验使用的算法在不同噪声下的分割结果。

3.2 医学图像分割

以BrainWeb 的第100 个脑MRI 图像作为实验，为充分地检测算法的抗噪性能及分割结果的精度，实验选取7%的噪声与40%的灰度不均匀图像。图5 为第100 幅脑MRI 图像的脑白质金标准图像、脑脊液金标准图像和脑灰质的标准分割图像。

图4 抗噪性实验结果Fig.4 Experimental results of noise immunity

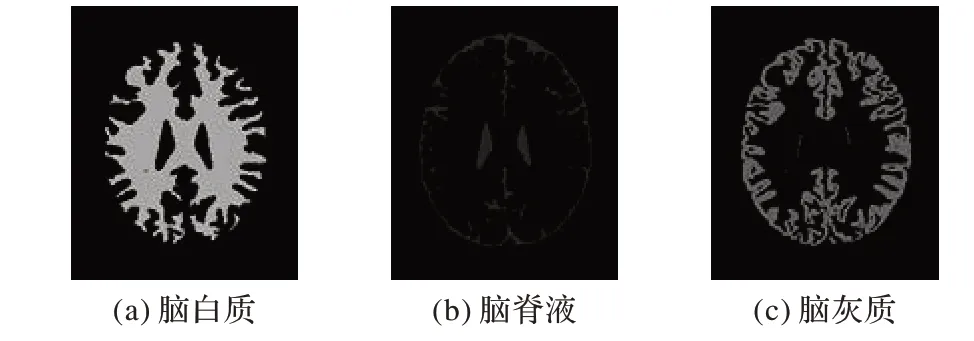
图5 标准分割图像Fig.5 Standard segmentation images

为进一步检测本文算法分割脑图像的精确度，实验选用以下5个指标进行评估:

1）JS（Jaccard Similarity）［19］，是用来评价算法分割准确的指数，是医学分割图像中使用最为广泛的指标之一。JS 的数值越大，代表聚类的性能越好，分割的精度越高，分割图像越靠近金标准图像。计算公式如下:

其中:S1为分割后的图像像素集和；S2为分割图像的标准图像像素集和。

2）Dice［20］，是一种使用很普遍的用于定量分析医学图像分割的精度的评价指标。Dice的值越大，分割后图像越好，图像分割越精确。计算公式如下:

其中:S1为分割后的图像；S2为标准分割图像。

3）Sensitivity［21］，是评价算法划分感兴趣区域能力的指标，其数值越大，分割效果越好，分割精度越高，分割图像越接近于标准分割图像。计算公式如下:

4）迭代次数，是指算法的迭代运行数，迭代次数的多少在一定程度上决定了算法的复杂度和性能，可以很好地说明算法的效率。

5）运行时间。为了客观地说明聚类运行时间的多少，选取FCM 迭代所用时间作为比较，尽管遗传算法的迭代运算需要一些时间，但经过优化后的聚类中心使得FCM 算法的收敛速度加快，在分割脑图像时所用时间并没有增加很多，而且对于高维数据具有更好的效果，使得算法的普适性更高。

实验后各脑组织图像分割结果如表3 所示，各脑组织的分割图像如图6所示。

从图6 可看出:本文算法的分割图像拥有更少的噪声点、更清楚的脑图像边界分割、更好的抗噪性能和更高的可靠性。从表3 可看出:本文算法相较于对比算法，在分割精度以及迭代次数上均有所提高。本文算法Jaccard 指数平均为82.76%，Dice 指数平均为90.45%，Sensitivity 指数平均为90.19%。与对比算法相比，本文Jaccard 指数分别提高了2.40 个百分点、2.10 个百分点、23.29 个百分点；Dice 指数分别提高了1.44 个百分点、1.26 个百分点、17.9 个百分点；Sensitivity 指数分别提高了1.86 个百分点、1.95 个百分点、16.95 个百分点。从表3 可以看出:本文算法在实验精度、迭代次数和运行时间整体更优，整体上提高了FCM 算法的效能，使得应用范围更广，能较好地分割脑图像，有效抵抗各种噪声和异常值；并且对高维数据拥有更好的实验结果，为更加精确地分割各脑组织提供了一种新的方法。

表3 脑组织图像分割结果Tab. 3 Brain tissue image segmentation results

4 结语

本文实验的主要目的是更精确地识别出脑图像中的WM、GM 和CSF 这三大组织，同时增强算法的抗噪性能，在整体上提升FCM 算法的效率，以及扩大其应用范围。通过改进算法的目标函数，引入马尔可夫随机场表示像素点的邻域信息以消除图像中像素点错误分类的结果，提高算法的抗噪性。由于FCM 容易受到初始值的影响，用遗传算法克服了这种缺陷，提高了聚类算法的分割的准确性，使得在图像分割中得到了很好的运用，鲁棒性高。实验结果显示，该算法拥有很强的抗噪声性，图像分割的准确性更高，能在一定的程度上减少了迭代次数，改善了FCM 算法的整体性能，为模糊聚类的划分应用提供了一种新的实践。下一步的研究方向是改善约束系数的自适应能力，将其应用于病灶图像的分割，以及提高算法的通用性。