基于多重网络的复杂产品工程变更传播影响评估

李从东，章志伟，曹策俊，张帆顺

（1. 暨南大学管理学院，广州510632； 2. 暨南大学物联网与物流工程研究院，广东珠海519070；3. 重庆工商大学商务策划学院，重庆400067）

（∗通信作者电子邮箱zhangzhiwei0123@163.com）

0 引言

工程变更是复杂产品设计过程中不可避免的重要活动。在产品全生命周期内，新的客户需求、生产制造工艺的改进、上下游供应链的变动等都会不断地要求企业对已有产品设计进行变更。特别地，对复杂产品而言，某个零部件的工程变更很可能影响到其他零部件，从而引发工程变更传播的连锁效应，甚至造成工程变更的雪崩式传播［1］。从这种意义而言，工程变传播可被视为各零部件为满足产品特定功能、行为、结构要求而发生的变更信息传递过程［2-3］。然而，在工程变更的实际执行过程中，产品设计人员往往只考虑了零部件间显性的结构关联关系，而忽略了其他的功能或行为关联关系。这很容易造成对潜在变更传播通道的忽视，进而导致变更活动的失控甚至失败。基于此，如何在综合考虑零部件间功能、行为、结构关联关系的情况下，对工程变更传播影响进行评估，从而提升复杂产品工程变更控制效果和效率是当前亟待解决的重要课题。

针对工程变更传播影响评估问题，国内外学者已进行了有意义的探索。从结构关联关系、功能和结构关联关系、功能-行为-结构关联关系三个视角，对已有文献进行梳理。基于结构关联关系视角，Lee 等［4］基于产品设计依赖网络，引入网络层次分析法测量零部件在工程变更影响和传播方面的相对重要性。Lee 等［5］使用贝叶斯网络对变更预测法（Change Predict Method，CPM）进行改进，以提高对各零部件变更可能性的预测精度。宫中伟等［6］提出利用INI 指数识别开发网络Hub 节点，并据此给出相应的工程变更控制策略。基于功能和结构关联关系视角，Zhang 等［7-8］提出在对工程变更影响评估过程中，需要利用零部件间结构和功能关联关系构造复杂产品零部件网络，以便对工程变更造成影响巨大的节点进行识别。郑玉洁等［9］将功能与结构关联关系细化为零部件的空间、物料、能力、信号依赖性，并用以构造产品关联关系网络，从而寻找最优变更传播路径。基于功能-行为-结构关联关系视角，Koh 等［3］证实在工程变更领域，零部件间功能、行为、结构关联关系是对复杂产品工程变更传播影响进行评估的必要信息。Hamraz 等［10］也提出利用领域匹配矩阵和多领域矩阵来匹配功能、行为、结构关联关系，以支持产品设计变更管理。总体而言，已有研究从不同视角、利用不同方法对工程变更传播影响评估问题进行了有意义的探索；然而，大多数已有研究在对复杂产品建模时仅考虑了功能、行为、结构关联关系中的部分类型，导致对工程变更传播影响评估的不准确。事实上，复杂产品工程变更的传播往往会在同一对零部件间多个功能、行为、结构关联关系内同时进行［3，10］。由于功能和行为关联关系具有隐蔽性和重叠性，任何对功能、行为、结构关联关系的忽视，都会造成潜在变更传播通道在一定程度上的遗漏，并且容易导致对变更风险的错误评估。换而言之，以上不足均会削弱工程变更控制的实际效果，甚至导致工程变更活动的彻底失效。

而随着多重网络理论的发展为解决上述问题提供了新思路和技术手段。具体地，复杂产品可以被抽象为一种多重网络:零部件作为网络节点，功能、行为、结构关联关系分别为不同网络层连边。不同于传统的单层网络，多重网络突破了连边同质性的限制，可以充分地反映出节点间多种关联关系［11］。在多重网络中，各类功能、行为、结构关联关系被独立地抽象出来并予以分层描述，使得以不同关联关系为载体的工程变更传播活动得到了全面的展示。特别地，考虑到多重网络模型中对各单层网络的聚合处理，能够将各层网络信息进行二次整合，而这对于功能、行为、结构关联关系的有机整合是至关重要的［10］。因此，在工程变更领域，采用多重网络模型对包含零部件及其功能、行为、结构关联关系的复杂产品进行建模是可行的。

针对上述问题，本文聚焦于基于多重网络的工程变更传播影响评估问题。首先，构建包括零部件功能层、行为层以及结构层网络在内的多重网络模型；其次，从节点的局部属性、全局属性、位置属性三个方面，评估节点重要度；最后，运用易感-感染-易感（Susceptibility-Infection-Susceptibility，SIS）模型对复杂产品工程变更传播影响进行定量化评估，试图为产品设计人员有效控制工程变更提供支持。

1 多重网络模型建立

1.1 基于FBS模型的关联关系分析

研究表明，功能-行为-结构（Function-Behavior-Structure，FBS）模型［12］常被用于系统地描述设计对象，其被相关领域从业者广泛接受。其中:功能代表设计目的；行为表示对功能实现过程的客观描述；结构指定设计对象的物理实体。从这种意义而言，作为具体设计对象，零部件为实现产品的特定功能，依托特定行为进行运作，受到特定结构限制。基于此，本文将零部件间的关联关系划分为三类:功能、行为和结构。

具体地，功能关联关系是一种较为抽象的零部件相关性，无法被设计人员感性认识，具有隐性特征。若多个零部件共同承担一项功能，即可视为彼此间拥有功能关联关系。在确定功能关联关系时，往往需要借助功能分析系统技术法、减件-运行法等手段获得形式化的逻辑推理结果。类似地，同样具有隐性特征的行为关联关系是一种对零部件间共同存在的行为的定性描述。一般地，零部件行为可由效应链推理法获得。然而，结构关联关系则是一种显性的直接物理连接关系，主要从几何、材料等维度展开对零部件相关性的描述，往往需要依靠各类物理规则对其存在性进行判定。

由于FBS模型是从产品概念设计视角对关联关系进行分类，为了将其合理地运用于产品全生命周期中，需要对各类关联关系进一步细分。鉴于文献［13］的观点，功能关联关系可被细分为物质流、能量流和信息流三种形式。对行为关联关系而言，其包含三类独立的隐性物理属性:机械、电特性和热效应。同样地，对结构关联关系而言，本文仅考虑有工程变更传播有关的因素，其被划分为四类独立的显性物理属性:几何、材料、表面和控制器。因此，如果同一对零部件至少共同承担一种形式的功能流、某种行为属性或某种结构属性，则该对零部件间存在相应的功能、行为或结构关联关系［10］。

在工程变更领域，对复杂产品进行建模后，还需要明确各关联关系所承载的变更传播风险［1］。事实上，变更传播风险是传播强度和传播范围扩散共同累积作用的结果，能够较好地表明关联关系所具备的传播特性。根据Clarkson 提出的变更预测法［14］，相邻零部件间变更直接风险被定义为变更发生直接可能性和变更直接影响的乘积。其中，变更直接可能性是指一个已变更零部件造成另一个相邻未变更零部件产生变更的概率，变更直接影响是指零部件发生变更时需要重做设计工作的平均比例。进而，变更传播直接风险可表示为:

其中:α表示关联关系的类型，α = 1，2，3分别代表功能、行为、结构关联关系；βα表示α 关联关系中的第β 类功能流或行为属性或结构属性，β1≤3、β2≤3，β3≤4；表示相邻零部件a和零部件b间关联关系α的下属第β类功能流或行为属性或结构属性所具有的变更直接风险；同理和为相邻零部件a 和零部件b 间关联关系α 的下属第β 类功能流、行为属性、结构属性所具有的变更直接可能性和变更直接影响。

为了充分展现复杂产品中各关联关系所承载的变更传播风险，可采用矩阵来表示，见图1。在设计结构矩阵（Design Structure Matrix，DSM）的基础上，分别构造变更直接可能性矩阵、直接影响矩阵以及直接风险矩阵。

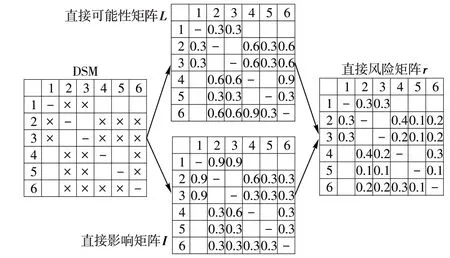
图1 工程变更直接可能性矩阵、直接影响矩阵和直接风险矩阵Fig. 1 Direct likelihood matrix，direct impact matrix and direct risk matrix for engineering change

图1中:左侧为1个包括6个零部件的产品DSM；“×”表示零部件间共同承载特定形式的功能流或者拥有相同的行为或结构属性。中间是以DSM 为基础得到的面向该产品零部件间某功能流或行为属性或结构属性的变更直接可能性矩阵以及直接影响矩阵，矩阵内部元素取值范围为［0，1］，其数值越大，表示对应零部件间的变更直接可能性、影响越大。右侧则是对应的变更直接风险矩阵。图1 表明变更直接可能性矩阵以及直接影响矩阵中的数据可以从工程变更数据库和产品设计人员处获取。特别地，根据相关数据进行估值时，应注意以下两点:第一，需要多名产品设计人员共同参与估值，且最终结果应是在各产品设计人员统一意见后所得出的唯一值；第二，面对历史数据，可以采用三角分布估计出具体数值。

1.2 多重网络模型

利用多重网络理论对具有M个零部件的复杂产品进行建模。该模型由三个单层子网（功能层、行为层和结构层）构成，每个单层子网均有相同的M 个节点，且连边仅代表一种关联关系。鉴于此，单层子网可用简单图描述为Gα=（V，Eα，Wα），其中:V是节点集合，用于表示零部件；Eα是连边集合，用于表示关联关系；Wα是连边权重集合，用于表示关联关系所承担的传播直接风险。进而，单层子网络可表示为:

图2 多重网络模型Fig. 2 Multiple network model

为进一步分析复杂产品中的关联关系，将其融入到单个聚合网络中。进而，聚合网络对应的邻接矩阵A =（aj，h）M×M，其内部元素可表示为:

考虑到变更直接风险是网络连边需要承受相应的工程变更信息流量负载的直观体现。信息流量负载越高，相应的变更直接风险也就越大。为了有效控制网络工程变更雪崩式传播的发生，应当赋予网络连边与其承担的变更直接风险相匹配的容量，故而聚合加权网络连边的权重可表示为（已对各子网络的权重值进行了归一化处理）:

例如，图3就是利用上述方法基于图2所获得的聚合加权网络。可以看出，聚合加权网络将多重网络中各单层子网有机地聚合在一起，虽然忽略了各连边在不同单层子网存在映射的事实，使得各连边在单层子网中的单独特性无法得到充分体现，但能够从全局的角度突出描述复杂产品的丰富拓扑结构，为准确计算节点重要度提供便利。

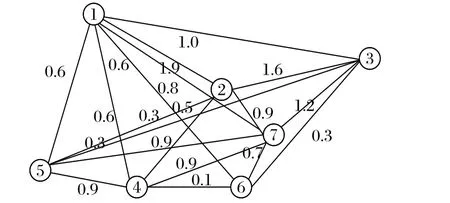
图3 聚合加权网络Fig. 3 Aggregation weighted network

2 节点重要度评价

2.1 全方位节点识别法

实际上，高重要度零部件在复杂产品拥有重要地位，在很大程度上能够控制变更传播走向以及变更传播影响范围［6］。因此，有必要对各零部件进行重要度评估，从而识别出高重要度零部件。然而，在复杂网络视角下利用各网络拓扑结构特征对各零部件对应的节点进行重要度评估是一个综合性问题，需要兼顾节点的全局属性、局部属性和位置属性［17］。

为了解决上述问题，本文引入全方位节点识别法。具体而言，Hou 等［18］将在不同重要度评估中综合得分较高的节点称为全面节点，并认为采用度、介数中心性、核度三个子指标得分的欧氏距离所生成的全面距离是识别全面节点的重要指标。因此，全面距离可表示为:

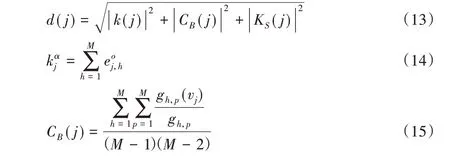
其中:d(j)表示节点vj的全面距离；k(j)表示节点vj的度，是局部属性；CB(j)表示节点vj介数中心性，是全局属性；KS(j)表示节点vj的核度，是位置属性；gh，p(vj)表示经过节点vj的节点vh到节点vp的最短路径数量；gh，p表示vh到节点vp的最短路径数量。此外，在介绍核度之前，需要了解到一个网络的K-核是指反复去掉度值小于KS(j)的节点及其连边后，所剩余子网的节点数量。若此时节点vj属于KS(j)-核，而不属于（KS(j)+1）-核，则节点vj的核度为KS(j)。

2.2 节点重要度衡量指标

然而，在现实场景中可以发现具有相同核度的节点，仍然会由于重要度的不同而获得差异化的信息传播能力，这表明核度不适合精确评估节点重要度。鉴于此，Liu等［19］依据目标节点与最高核度节点集的最短距离，构造出基于节点位置属性的重要度测量指标（简称K-核距离）:

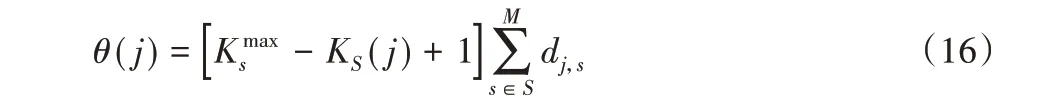
其中:θ(j)表示目标节点vj的K-核距离；Kmaxs是网络核度，即网络中的最高核度；dj，s表示节点vj到节点vs的最短距离，也就是节点vj和节点vs间所有连通的路径中权重倒数之和（本文中权重为相似权）的最小值；S 为具有网络核度的节点集合，则s表示拥有网络核度的节点。可以看出，K-核距离指标能够依托节点最短距离计算目标节点到达各具有网络核度的节点距离，从而体现目标节点在网络中的传播影响力。

基于上述分析，为了提升全面距离对同核度节点重要度的区分能力，本文将K-核距离融入到全面距离中，生成改进的全面距离指标（下文简称改进全面距离）:

可知，改进全面距离越高，表明目标节点相邻节点数量越多、经过的最短路径越多、达到其他高重要度节点的最短距离越短，进而目标节点所对应的零部件在变更传播过程中越容易被影响且引起的变更传播影响范围越大。因此，基于工程变更视角，可认为改进全面距离适用于衡量复杂产品的零部件重要度。

2.3 节点重要度评估算法步骤

根据前文中对节点重要度评估的描述，给出节点重要度评估算法，步骤总结如下:

Step1 根据各节点间的变更直接风险，由式（6）、（7）、（9）计算聚合加权网络中各连边权重；

Step2 利用聚合邻接矩阵，根据式（14）求得聚合加权网络中各节点度；

Step3 基于聚合加权网络，使用Dijkstra 算法，求出所有节点彼此间最短路径，其后利用式（15）求解其介数中心性；

Step4 利用K-核分解方法，求得各节点核度，并根据式（16）求得各节点的K-核距离；

Step5 根据式（17），算出各节点的重要度。

3 基于SIS模型的节点重要度评估方法验证

为了验证改进的全面距离指标的有效性，本章采用易感-感染-易感（Susceptibility-Infection-Susceptibility，SIS）模型对具有最高重要度的节点进行传播能力分析。SIS 模型常被用于描述流行病的传播过程。在每个时间步内，感染节点会以概率λ 感染易感邻居节点，同时会以概率β 重新变为易感节点。而在工程变更传播过程中，已变更零部件会对相邻未变更零部件进行变更传播，并且已变更零部件也会发生反复变更迭代，这与SIS 模型所描述的流行病传播过程相类似。进一步地，为了使SIS 模型能够应用于加权网络，考虑连边权重对传播速率的影响，定义感染节点vj感染易感邻居节点vn的概率为:

其中:η 和θ 均为大于零的常数。为了不失一般性，在本文中设η = 0.2，θ = 0.6，并给出在t时间步时，度为K（j）的易感节点vj被感染的概率［20］:j

其中:Nj(t)表示在t时间步内节点vj的感染邻居节点vn集合。

在验证过程中，对初始感染源的确定，除了利用度、介数中心性、K-核距离、全面距离和改进的全面距离指标外，还考虑了随机选择节点和遍历寻找两种情况。在随机选择情况下，是将任意选取的单个节点作为感染源，以运行SIS 模型。而在遍历寻找情况下，将所有节点分别作为感染源运行SIS模型，在确定最优感染源后，将其传播结果作为最终结果。理论上，遍历寻找可以确定网络中重要度最高的节点，但其运算非常耗时并不适用于实践，此处仅作为验证手段。

由于复杂产品具有较高的连通性、聚类性和异质性，为了尽可能地贴近现实环境，分别以随机生成拥有500 个节点的NW 网络和BA 网络为仿真基础。而考虑到现实复杂产品工程变更过程中，零部件即使在发生某次变更后，仍然会因受到其他零部件变更影响而导致再次变更，故而在SIS 模型中设由感染状态恢复为易感状态的概率β = 1。此外，仿真环境为双核Intel Core i5-5200U/Matlab（2015b）。进而，分别在NW 网络和BA 网络中运行SIS 模型40 次后，求得基于相应的7 种初始感染源，各感染过程中在不同时间步内平均感染节点数量（见图4）。从图4 可以看出，在NW 网络中和BA 网络中，以改进的全面距离最高的节点为初始感染源，获得的感染节点数量均仅次于遍历寻找情况下所获的结果，且两者间的差距较小。结果表明，改进的全面距离指标可以获得较好的重要节点确认结果。由此可以认为，在无法运用遍历寻优的现实环境中，改进全面距离指标可以有效识别网络中的最重要节点。而从广义上来说，改进全面距离指标同样能够对各节点重要度进行有效且合理的评估。

图4 基于不同网络的SIS模型仿真对比Fig. 4 Simulation comparison of SIS models based on different networks

4 案例分析

柴油发动机是一种典型的复杂机械产品，在实际研发过程中常需要根据不同规格载具的要求进行工程变更。本文以某型号载货汽车的柴油发动机为研究对象，在保留40 种主要零部件的基础上，对本文方法的可行性和有效性进行验证。

1）对柴油发动机零部件间FBS 关联关系进行分析，得到的传播直接风险矩阵（见图5）。

2）将图5 中所展现的传播直接风险矩阵表示为多重网络，并最终形成聚合加权网络，相应结果如图6所示。

3）根据第2 章的描述，构建节点重要度评估指标。在由式（17）计算各节点的改进全面距离后，将其按从大到小进行排序，从而作为节点重要度评估结果（见表1）。若取表1中排名前5 的节点为高重要度节点，则本案例中高重要度节点依次为2、11、1、17、9。

4）为验证上述高重要度节点的正确性，将其与采用度、介数中心性、K-核距离、全面距离以及遍历法获得的高重要度节点进行比较。此处，在运行SIS 模型时，同样将式（18）中的随机常数η 和θ 设置为0.2 和0.6，并且将β 设置为1，则具体结果如表2 所示。进一步地，为验证改进全面指标对非重要节点的排序正确性，分别以节点2、11、1、17、9 为初始节点进行变更传播过程仿真，相关结果见图7。

由上述验证过程及其结果可知:

1）通过对比图6（a）、（b）可以发现:聚合加权网比单层功能、行为、结构关联关系网具有更加丰富的拓扑结构。虽然，单层功能、行为、结构关联关系网络可以在其领域范围内提供一定的零部件关联关系信息，但这些信息并不完整，容易导致对零部件间总体变更直接风险的错误预测。因此，将以FBS关联关系为连边、零部件为节点的多重网络应用在工程变更领域中是合理性且有必要的。

2）由表2 可知，利用改进全面距离所获得的最高重要度节点与利用度、介数中心性、全面距离以及遍历寻找所获得的最高重要度节点相同，均为节点2。这与事实相符:气缸体作为柴油发动机的主体零部件是多数零部件的直接承载体，在结构、行为和功能上必然与其他零部件间存在大量关联关系。在工程变更传播过程中，气缸体受到变更传播影响的概率较高，且对变更的传播能力较强，相对于其他零部件具有更高的重要度。此外，利用改进全面距离所得到的高重要度节点集与度、全面距离指标、遍历寻找所获得的高重要度节点集节点相同，由此可以再次验证本文方法的有效性。而上述节点集所存在的节点排序差异是由于利用不同指标评估节点重要度时需要考虑的因素和利用的算法不同所造成的。例如，观察表2 可以发现相较于节点11，虽然节点1 的度、K-核距离要更高，但其介数中心性要明显更低。由于节点1 的相邻节点数量要高于节点11，到其他最高K-核节点的距离也比节点11更短，然而经过该节点的最短路径数量要远低于节点11。这意味着从改进的全面距离指标视角来看，在最终考虑传播能力时，节点11要强于节点1。

图5 柴油发动机各关联关系的传播直接风险矩阵Fig. 5 Propagation direct risk matrix for each diesel engine association relationship

3）由图7 发现当更传播时间步超过某一阈值时，发生变更的零件数量趋于稳定，即接近全部零件数。在图7 中，多数零部件变更传播过程，会在第11～13时间步趋向稳定。因此，在产品工程变更传播过程中如果不能及时控制变更传播，则工程变更传播将会影响到整个产品范围，最终导致整个产品工程变更传播控制效果和效率大打折扣。

总的来说，为了尽可能地降低复杂产品的工程变更传播影响，需要以高重要度零部件为对象，执行以下三种工程变更控制策略:

1）增加高重要度零部件设计余量。零部件的设计余量是该零部件所承载功能流或行为属性或结构属性的允许值和实际值间差值。存在设计余量的零部件在工程变更传播过程中可以充当变更缓冲区，以吸收传播直接影响，从而降低甚至消除与未变更相邻节点间的传播直接风险。因此，在复杂产品原始设计中，适当增加高重要度零部件的设计余量是极其有必要的。

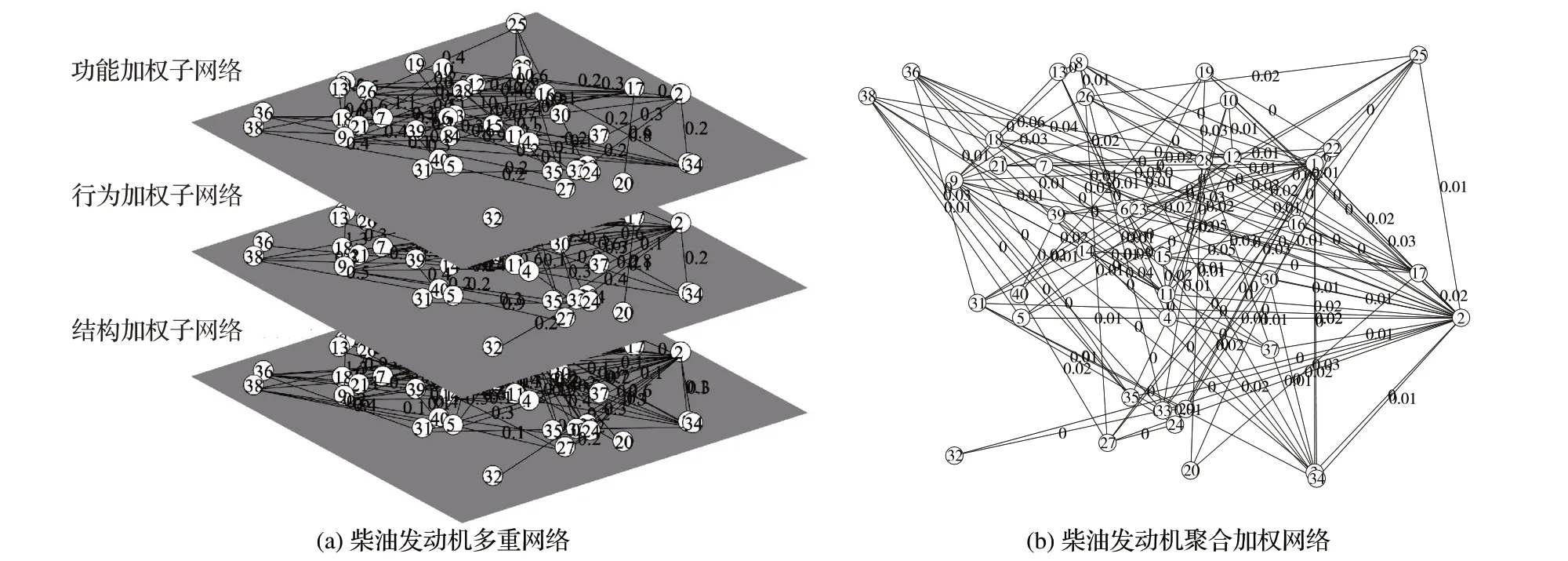
图6 柴油发动机多重网络模型Fig. 6 Diesel engine multiplex network model

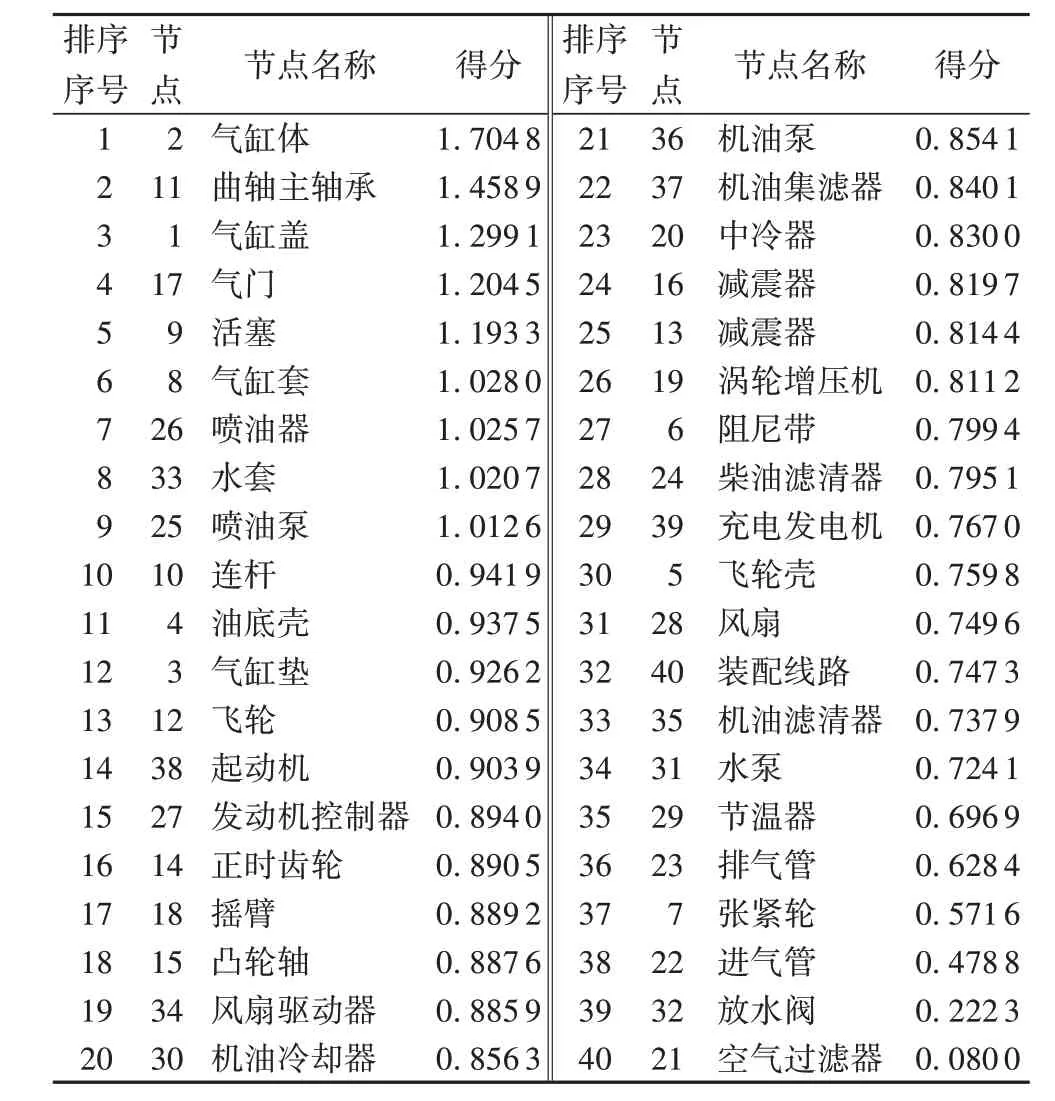
表1 柴油发动机多重网络节点重要度评估Tab. 1 Evaluation of importance degrees of multiplex network nodes for diesel engine

2）采用模块化设计思想，将高重要度零部件尽可能地聚集在特定模块内。在工程变更发生时，使不同模块间高重要度零部件存在较少关联关系，可以将工程变更限制在特定模块内部，而不波及到其他模块。然而，为防止工程变更通过此类关联关系在各模块间进行传播，对各模块接口零部件间长程连接所对应的关联关系进行限制仍然是有必要的。

3）降低或消除高重要度零部件与其他零部件的变更传播可能性。针对高重要度零部件:首先，可以直接断开或削弱其与相邻高重要度零部件间关联关系，以减少高重要度零部件间相互影响；其次，在确定高重要度零部件设计余量后，通过增加高重要度零部件与非高重要度相邻零部件间的连接，缓解其变更压力，降低变更信息传递量。

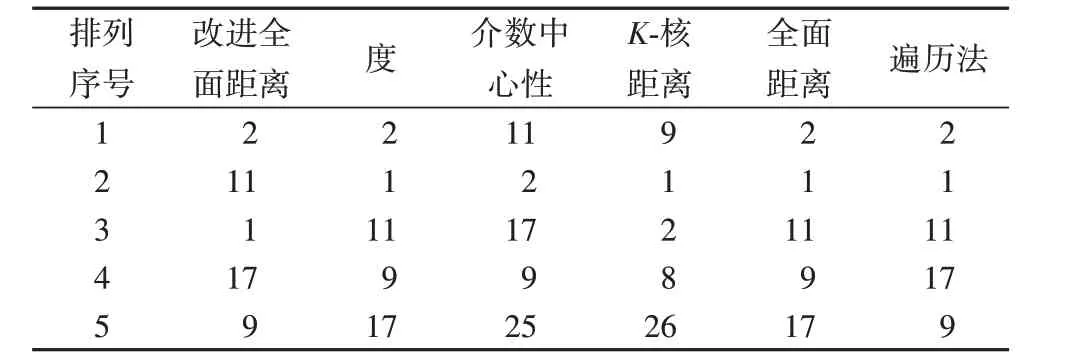
表2 不同指标/方法求得高重要度节点对比Tab. 2 Comparison of high-importance nodes obtained by different indicators/methods

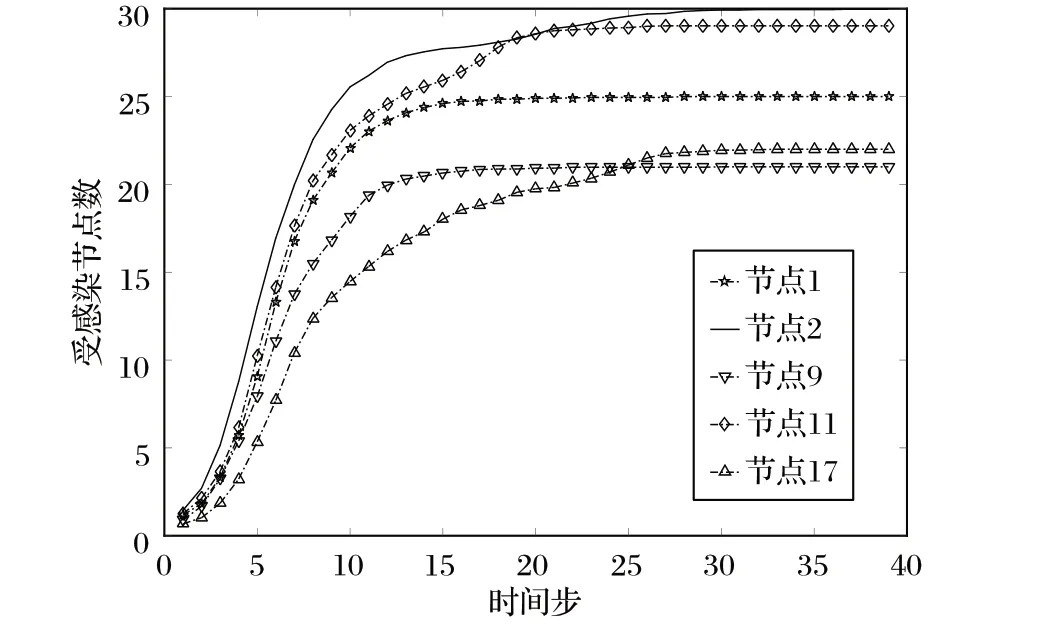
图7 重要节点感染模型Fig. 7 Important node infection model

5 结语

对复杂产品中特定零部件进行工程变更极有可能导致其他零部件的连锁变更，甚至造成变更的雪崩式传播。为了降低发生雪崩式传播的风险，如何在综合考虑零部件FBS 关联关系的情况下对工程变更传播影响进行评估是工程变更领域的一个关键问题。本文首先引入多重网络对复杂产品进行建模，详细地描述了产品内部零部件及其FBS 关联关系；接着，构建改进全面距离评估各节点重要度；最后，利用SIS 模型验证了改进全面距离指标的有效性，以实现对工程变更传播影响的有效评估。

本文考虑了复杂产品各零部件分别在功能、行为和结构层面的产生关联关系，而额外考虑各零部件因功能、行为和结构相互映射所生成关联关系的复杂产品工程变更传播影响评估问题将是接下来的工作。与此同时，本文所针对的是以单个零部件为初始变更起源的复杂产品工程变更，考虑多个初始变更起源情况下的复杂产品工程变更传播影响评估问题是有意义的。此外，作为一个有价值的主题，另一有希望的研究方向就是将本文方法融入到特定软件或平台中，以便为产品设计人员进行复杂产品工程变更工作提供准确的指导性建议。因此，本文的后续工作之一就是创建基于多重网络和FBS 模型的工程变更传播影响评估系统，从而将本文方法更加深入地应用于实践中。