基于自适应深度迁移学习的多孔介质重构

陈 杰，张 挺*，杜 奕

（1. 上海电力大学计算机科学与技术学院，上海200090； 2. 上海第二工业大学工学部，上海201209）

（∗通信作者电子邮箱bee921@163.com）

0 引言

多孔介质重构［1］在石油地质勘探、地层学和岩石学的研究等诸多领域有着大量的应用，多孔介质模型可以用于定量研究多孔介质内部各种微观因素（如孔隙结构、润湿性、含水薄膜）对储层宏观性质的影响，它对研究储层油气充注过程和油气渗流机理有关键作用，所以建立一个准确客观的三维多孔介质重构模型对石油和天然气勘探以及岩层研究有着重大意义。随着实验仪器的创新和新理论、新技术的突破，国内外研究团队不断提出新的多孔介质重构的方法，主要分为物理实验方法和数值重构方法等［2］。

物理实验方法使用实验仪器扫描多孔介质样品获得大量的二维截面，然后通过建模程序形成三维多孔介质，但是设备使用成本高、实验困难。

与物理实验方法不同，数值重建方法［3］通常基于少量的二维或三维真实图像，并通过随机模拟或沉积岩过程模拟重构三维多孔介质。与物理实验方法相比，虽然这些方法成本低，可以重构多种多孔介质，但耗时长，不能很好地重构页岩等内部结构复杂的多孔介质。

多点统计法（Multiple-Point Statistics，MPS）［4］被认为是重构多孔介质和随机模拟的典型数值方法，通过使用训练图像（Train Image，TI）来计算条件累积概率函数。然而，MPS 模拟速度慢且对内存要求高，模拟过程复杂。

深度学习（Deep Learning）［5］从问世起就倍受学术界和工业界的关注，它可以获取高维数据中的复杂结构特征。将深度学习的相关技术应用到多孔介质重构的建模方法中，有助于提取训练图像的复杂结构特征。深度迁移学习（Deep Transfer Learning，DTL）［6］是深度学习领域的重要技术之一，它可以将在其他数据集中已经训练好的模型快速转移到另一个数据集上。DTL 可以视为深度学习和迁移学习的结合，在深度学习提取多孔介质的结构特征后，利用迁移学习将学习到的特征用于新的多孔介质重构结果中，使其能够很好地拟合新的数据集，达到良好的效果［7］。

本文提出一种基于自适应深度迁移学习的多孔介质重构方法——ADTL（Adaptive Deep Transfer Learning），在多孔介质重构的建模过程中，不再对每一个未知点进行概率统计，在深度学习的隐藏层中加入一些自适应迁移层以减少来自不同多孔介质数据的分布差异。通过梯度下降学习训练图像的全部特征，然后再使用深度迁移学习将学习到的特征迁移到建模区域。

ADTL方法在重构过程中分为两个重要阶段:第一阶段是训练深度神经网络，通过梯度下降找到合适的参数来完成训练图像特征的学习；第二阶段是将深度神经网络学到的特征复制到新的重构结果中。

与传统的模拟方法（如MPS）相比，由于采用了显卡加速和深度学习的优化算法，可大大缩短ADTL 的处理时间。另外，传统方法不能将重构特征以参数形式存储在磁盘上，所以每次重构都要重新扫描训练图像，非常耗时。而ADTL 方法在训练一旦完成后，学习到的特征能够以参数的形式存储在硬盘中，所以可以重复利用，不必每次重新扫描训练图像，因此速度优势明显。

实验针对砂岩数据使用ADTL 方法进行重构，并通过比较重构结果和训练数据多点连通曲线、变差函数曲线和孔隙度，评估了该方法的性能。实验结果表明，ADTL 方法的重构结果很好地保留了训练图像的结构特征，提高了重构的效率；而且与传统的MPS 比较发现，ADTL 方法在重构质量、重构速度和内存占用方面具有优势。

1 自适应深度迁移学习

1.1 深度学习

深度学习也称为深层神经网络，最初在1986 年被引入机器学习，深度学习就是基于神经网络，使用许多简单的非线性特征把原始数据转化为更复杂的数据表达［8］。

深层神经网络构造如图1 所示，每层由若干神经元组成，X（x1，x2，…，xi）表示输入特征向量，y 表示输出预测值。训练学习复杂任务时，每一层的网络节点没有数目要求，但是应设置较多的隐藏层。在前馈神经网络中隐藏层为全连接层；在卷积神经网络中，隐藏层可分为卷积层和全连接层。所有这些隐藏层中，排序较前的几层能够学习一些低层次简单特征，排序较后的几层能把简单的特征结合起来，学习更为复杂的任务［9］。

对于深层神经网络模型，损失函数可以衡量算法在单个训练样本中的效果，对于所有的训练样本，需定义一个损失函数，如式（1）～（2）所示:

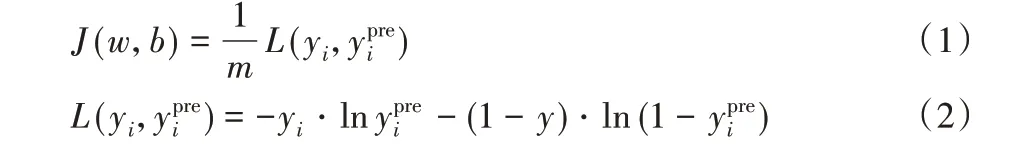
其中:m、w 和b 分别表示输入数据样本的数量、神经元中的权重和偏差；i=1，2，…，m，表示输入数据的数量；yi和yipre分别表示数据输出的真实值和预测值。神经网络反向传播［6，9］时更新w、b 和J（w，b），在训练模型过程中，找到合适的w 和b 来使得总损失函数J（w，b）最小。具体方法就是通过前向传播［10］和反向传播的迭代。

前向传播时，对于每一个隐藏层，

其中:z 是每个隐藏层的输出；a 是z 经过激活函数后的输出；l为隐藏层序号（如z［l］表示第l层的输出z）。

反向传播时是通过链式求导完成参数迭代，如式（5）～（8）所示:

其中:α为学习率。

图1 深层神经网络模型Fig.1 Deep neural network model

1.2 深度迁移学习

迁移学习是由机器学习技术发展出的一种方法，主要是为了将机器学习领域已有的经典模型或者已经训练好的模型用到新的领域和任务中，这样可以不必对每一个新任务都重新训练一次模型，不仅节省时间而且提高了模拟效率，降低了训练数据需求量［11］。

对于许多需要使用迁移学习的任务，在迁移的来源任务中有很多数据，而迁移的目标任务中数据很少。如果想从源任务中学习并迁移一些知识到目标任务中，那么源任务和目标任务需要有同样属性的输入。目标任务中的数据是想要拟合的数据，但其中真实数据的量一般较少，那么迁移学习可从一些目标相似度高并且拥有大量数据的源任务中获得低层次的特征，然后将这些特征在目标任务中复现［12］。深度迁移学习就是在使用深度学习时加入迁移学习方法。

1.2.1 Finetune

Finetune［13］是一种深度迁移学习方法，它在进行深度迁移学习时，固定训练模型的全部卷积层和部分全连接层，只训练自己定制的部分全连接层。图2 所示为一个深层神经网络的结构图，它是由输入层、输出层和隐藏层组成。深度迁移学习Finetune 的过程，就是将输出层前面的一个或者几个隐藏层定义为迁移层Ltransfer，如图2所示；迁移层前面的隐藏层和输入层定义为固定层Lfixed（包含卷积层和全连接层）。将已训练完成的深层神经网络结构中的迁移层Ltransfer进行随机初始化操作，然后使用新的数据对整个网络进行重新训练，但每次前向传播和反向传播时不改变固定层Lfixed的参数，而是仅仅对迁移层Ltransfer和输出层进行参数迭代，完成训练后，原来的迁移层（浅色部分）变成了新的网络层（深色部分）。图2 中固定层和新的迁移层组合起来就是迁移完成以后完整的神经网络结构。

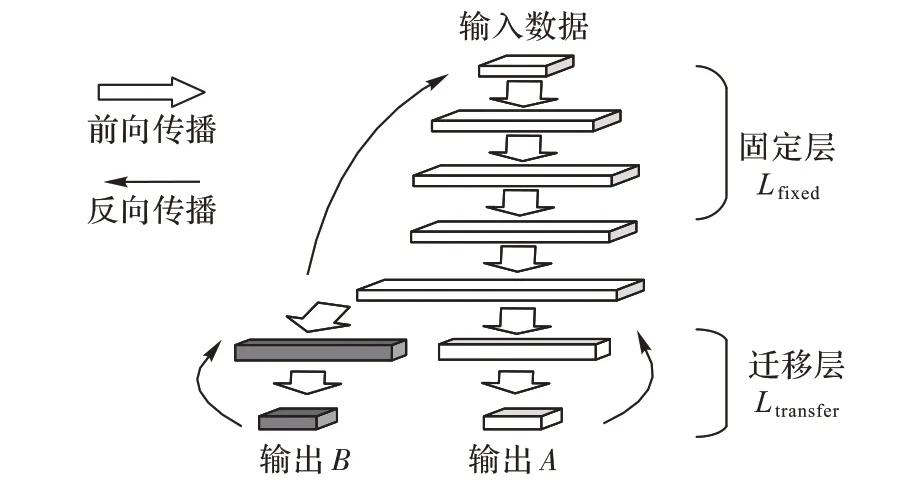
图2 深度迁移学习结构Fig.2 Structure of deep transfer learning

1.2.2 自适应深度迁移学习

因为Finetune 在训练数据和测试数据分布相差较大的情况下效果较差，本文通过在深度学习迁移方法中加入自适应层（Adaptation Layer）［14］来完成源域和目标域数据的自适应，使得它们的数据分布更加接近，迁移效果更好。

如图3 所示，在原本的迁移层中加入自适应层，然后进行Finetune。加入自适应层后，网络的总损失为:

其中:L（yi）是网络在数据集上的损失函数；L（Ds，Dt）是网络的自适应损失，添加自适应损失的目的是在进行梯度下降时减少因不同数据分布差异导致的训练结果不理想；λ 是自适应系数［14］；Ds和Dt分别表示源数据和目标数据。

图3 自适应深度学习结构Fig.3 Structure of adaptive deep learning

通过添加自适应层提高深度迁移学习的学习效果，但额外增加了计算复杂度，并且在设计自适应层时较为繁琐［15］。文献［16］中将自适应层替换为BatchNorm 自适应层，从而加入统计特征的适配性，这种方法称为AdaBN（Adaptive Batch Normalization）［16］，属于自适应迁移学习。

AdaBN 实现简单而且该方法不增加额外的参数，降低了重构的复杂性。只需将图3 中的自适应层替换为一种新的数据层（称之为BatchNorm 自适应层），然后进行Finetune。加入AdaBN 作用是解决来自不同数据集样本的数据分布差异，AdaBN使用更新算法将数据集中的样本标准化为零均值和同方差，从而缓解不同数据集的位移问题［16］。

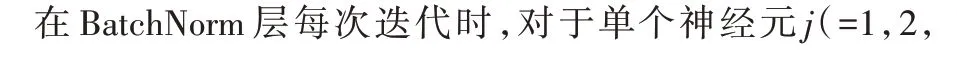
其中:yj是神经元j 的输出；xj为输入；μj和σ2j分别为计算均值和计算方差。

对于第n 次迭代时输入的m 个样本，其输入均值和输入方差分别为μ和σ2。此时计算均值μj和计算方差σ2j的更新规则为:

其中:d 是第n 次迭代的输入均值μ 与第n - 1 次迭代的计算均值之差；Nj是前n - 1 次迭代时所有的样本数之和，即累计样本数；运算符“←”表示每次迭代时更新符号左边的数据。在第一次迭代时，μj和被分别初始化为0和1。

2 ADTL方法流程

本文提出使用深度学习来整体提取训练图像中的结构特征，替代传统的模拟方法（如MPS）扫描训练图像这一过程，然后使用自适应深度迁移学习中的AdaBN 方法将提取到的特征复制到模拟结果中，最终可以得到具有训练图像结构特征的重构结果。

算法具体步骤如下:

步骤1 首先从训练图像中获取全部数据，为了加快深度学习的训练速度和防止梯度爆炸，对数据进行随机排序、归一化等处理，得到数据集DS。

步骤2 设计深层神经网络的结构，并将深层神经网络结构划分为固定层Lfixed、迁移层Ltransfer和输出层Lout，在迁移层中加入BatchNorm自适应层。

步骤3 使用设计好的深层神经网络对训练图像数据进行迭代拟合来学习其中的复杂特征，当训练误差达到要求时训练结束，得到模型TS。TS中保存了神经网络结构中每一层的权重w和偏差b。

步骤4 利用真实条件数据形成数据集DT，并在DT上对深度学习模型进行迁移学习。进行迁移学习的方法为:随机初始化迁移层Ltransfer的所有参数，然后加入DT进行训练，训练神经网络时保持固定层Lin参数不变，每次前向传播和反向传播时仅改变迁移层Ltransfer和输出层Lout的参数，当总代价满足要求后训练完成，得到模型TT。

步骤5 将数据集DS的输入特征向量作为模型TT的输入，就得到了预测值，这些特征向量和对应预测值即为重构结果。

3 实验与结果分析

3.1 重构质量评价标准

评价多孔介质重构结果优劣的标准与一般重构方法有较大的不同。一般重构方法中的重构数据与原始数据的相似度是由两者在每个相同位置具有相同状态值的元素的比例决定的。在一般重构方法中，该比例越高，重构相似度就越高，但是这个判定标准对于多孔介质重构并不适用。多孔介质重构并不要求随机模拟结果与训练图像完全一致，它的真正作用体现在捕捉训练图像的结构特征，并将这些特征复制到重构数据中，这些结果是对训练图像结构特征的反映，重构效果的优劣在于这些结构特征是否被复制到重构数据中。

因此，本文评价重构结果时并不直接比较重构结果和训练图像是否相同，而是通过多个重构结果的孔隙度、变差函数［17］，以及连接性曲线来衡量。

3.2 训练图像和真实图像

本文利用砂岩图像重构来验证本文方法的有效性，即使用深度学习对砂岩训练图像的孔隙结构特征进行学习，然后使用自适应迁移学习将这些特征和真实数据结合，完成砂岩图像的重构。首先使用同步辐射扫描获得砂岩数据（底面半径为500 体素，高为1 022 体素的圆柱体砂岩），再从该砂岩不同位置随机截取两份80 × 80 × 80 体素的体数据分别作为训练图像与真实图像，孔隙度分别为0.174 5 和0.176 3。真实图像是指客观存在的真实数据图像，是实验中需要模拟的目标，用来与模拟结果进行对比。由于训练图像与真实图像从同一块砂岩提取，故可以认为它们具有相似的孔隙结构特征，如图4～5所示。

图4 训练图像Fig.4 Training image

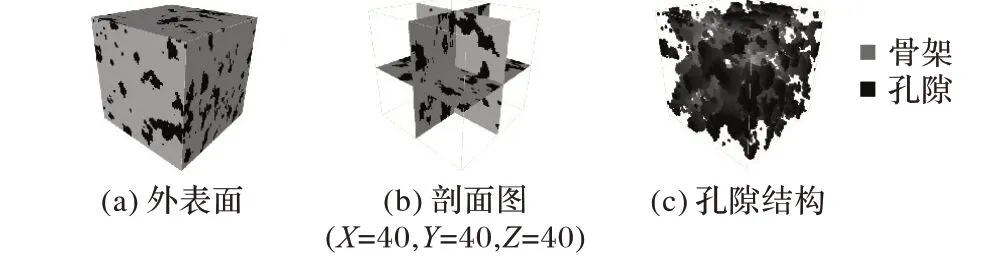
图5 真实图像Fig.5 Real images

图4（a）是训练图像的外表面，图中深色表示孔隙，浅色表示骨架；图4（b）是训练图像正交剖面图；图4（c）是将砂岩骨架隐藏后的孔隙结构图。从图4 可知，训练图像的孔隙特征具有长连通性，并且有不规则的孔隙形状。图5（a）是真实图像的外表面，图5（b）是其剖面图，图5（c）是其孔隙结构图。通过对真实图像进行随机采样，得到了0.5%的点作为重构图像的条件约束数据，其中孔隙点占采样点的比例为0.174 2。

重构目标是使得重构图像的孔隙结构与真实图像的孔隙结构相似。数据集的输入是1× 3 的输入矢量X，矢量的每个维度的取值范围｛j=1，2，…，80｝，其中xij=｛x1j，x2j，x3j｝为X 的三个特征向量，Y=｛0，1｝为砂岩的结构值，0 表示骨架，1 表示孔隙。真实图像采样数据量和训练图像数据量分别是2 560 和512 000。

3.3 ADTL与传统MPS方法对比

3.3.1 孔隙度对比

实验中，深层神经网络的输入特征为每一个砂岩点的空间位置信息，每一个点的标签值使用0表示骨架，1表示孔隙，通过ADTL 方法得到一个重构图像结果（80 × 80 × 80 体素），如图6 所示。图6（b）的孔隙在不同截面上呈现出不规则形状，而图6（c）孔隙具有训练图像中孔隙长连通性的特征。ADTL 方法重构图像的孔隙度为0.175 2，与真实图像的孔隙度是十分接近的。

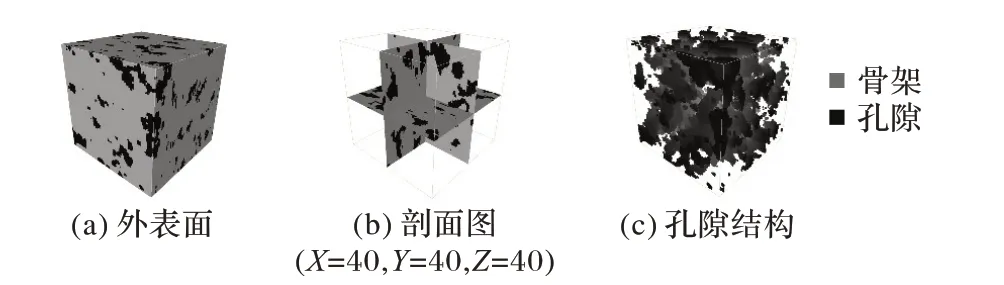
图6 ADTL重构图像Fig.6 Images reconstructed by ADTL

为了与其他经典重构多孔介质方法比较，又采用传统的重构方法MPS 来对砂岩孔隙图像进行重构，分别使用ADTL和MPS 进行了10 次重构来验证结果。图7 是MPS 方法得到的一个重构图像，该MPS重构图像孔隙度为0.171 9。

图7 MPS重构图像Fig.7 Images reconstructed by MPS

对比真实图像、ADTL 重构图像和MPS 重构图像可看出，三种重构图像在孔隙结构上均较为相似。表1 是MPS 和ADTL重构图像10次的重构结果平均孔隙度，可见ADTL方法生成的图像与真实图像的孔隙度更为接近。

表1 MPS和ADTL重构图像的10次重构结果平均孔隙度与真实图像的平均孔隙度Tab. 1 Average porosities of 10 reconstruction results of DTL and MPS and average porosity of real image

表2 是MPS 和ADTL 方法分别进行10 次重构的图像孔隙度，可以看出ADTL 方法的结果方差较小，说明波动较小，更为稳定，孔隙度分布更集中。

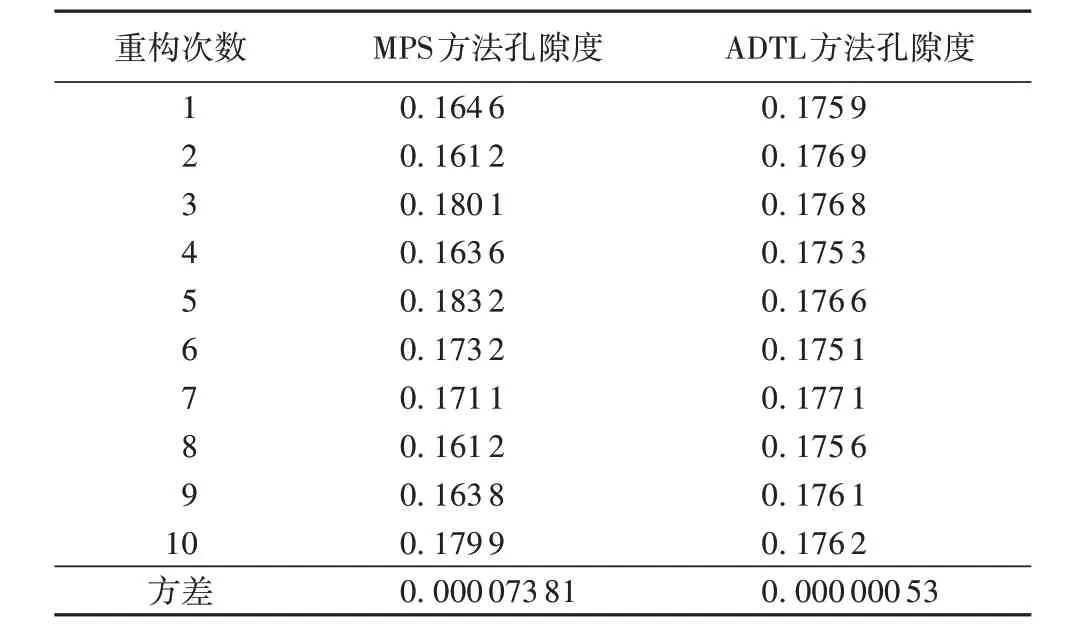
表2 MPS和ADTL方法10次模拟重构图像的孔隙度Tab. 2 Porosities of 10 reconstruction results of DTL and MPS

3.3.2 变差函数对比

变差函数（Variogram）是评价多孔介质重构图像效果的重要工具，计算公式见文献［18］。设X、Y 和Z 方向上相邻点之间的距离为1，变差函数的每对计算点之间的距离（单位:像素）作为变差函数曲线横坐标。分别计算真实图像、MPS重构图像和ADTL重构图像在X、Y、Z方向的变差函数，如图8所示。ADTL 重构图像与真实图像在X、Y 和Z 方向变差函数的变化趋势都更加相似，说明二者的孔隙结构特征更相近。

3.3.3 连接性曲线对比

变差函数能够反映空间变化特征，但不足以表征多孔介质结构的多点相关性。多孔介质重构方法使用多点连接性（Multiple-Point Connectivity，MPC）［18］来评估重构结果。图9所示是真实图像、MPS 重构图像和ADTL 重构图像在X、Y、Z方向的MPC。在X、Y 方向上ADTL 方法的效果略优于MPS 方法，在Z方向上ADTL方法明显优于MPS方法。

图8 MPS、ADTL重构图像及真实图像的变差函数Fig.8 Variograms of real image and images reconstructed by MPS and ADTL

图9 MPS和ADTL重构图像及真实图像的多点连接性曲线Fig.9 MPC curves of real image and images reconstructed by MPS and ADTL

3.3.4 内存和CPU性能对比

由于ADTL 方法在建模时主要使用计算机的GPU 进行模拟，相较于MPS 方法对内存和CPU 的使用更少，这使得该方法在模拟时对计算机的性能影响较小。

本文实验环境:CPU 型号为Inter Core I7-8700 3.2 GHz，内存8 GB，GPU 型号为Nvidia GeForce GTX 1070（6 GB）。分别对两种方法10 次重构过程的内存占用和CPU 使用率以及耗时进行记录，然后求取平均值。如表3 所示，使用ADTL 方法对内存和CPU 的占用远小于MPS 方法。ADTL 方法耗时同样明显少于MPS方法，说明ADTL方法效率更高。

4 结语

本文提出了一种基于自适应深度迁移学习的多孔介质重构方法，通过对三维结构进行一个整体的学习，使其重构结果

在三个维度均能取得良好的效果。由于传统多孔介质随机重构（例如MPS 方法）建立的模型不是唯一的确定性模型，而是一系列的等概率随机实现，所以可能需要多次建模得出平均结果，且这些结果方差较大。而本文方法的神经网络建模过程是一个寻优学习的过程，建模时不容易陷入局部最优，得到的结果更为稳定，因此更有优势。实验结果表明在多孔介质重构建模中，使用自适应深度迁移学习得到的重构结果精度更高、连通性和结构特征更好，内存和CPU 的占用以及模拟耗时也远低于传统方法。