基于微基站发射功率的异构蜂窝网络能效优化

陈永红，郭莉莉，张士兵，杨 洁

（1. 南通大学杏林学院，江苏南通226000； 2. 南京邮电大学通信与信息工程学院，南京210003；3. 南通大学信息科学技术学院，江苏南通226019； 4. 南京工程学院信息与通信工程学院，南京211167）

（∗通信作者电子邮箱yangjie@njit.edu.cn）

0 引言

异构蜂窝网络（Heterogeneous cellular Network，HetNet）被广泛认为是移动数据流量爆炸性增长的一种解决方案。异构蜂窝网络中各层基站的空间密度、发射功率、支持速率均不相同。基于随机几何的异构网络研究引起了人们的广泛关注。文献［1］为异构网的下行链路分析提出了一个精确的模型，该模型由K层随机部署的基站构成，其中每层在平均传输功率、数据速率和基站密度方面都不同。在该模型的基础上，对多层HetNet 的研究陆续展开［2-5］:层间频谱分配策略、最优网络部署与扩展、小区接入策略分析、多层异构蜂窝网的干扰管理技术等。这些研究结果均是基于均匀泊松点过程（Poisson Point Process，PPP）模型进行分析的。虽然泊松点过程已被广泛用于无线网络的空间配置建模，但是将所有的基站建模为互不相关的空间分布确实与实际系统不符。考虑到宏基站（macro base station，MBS）发射功率大、覆盖范围广，MBS的部署通常呈现一定的相斥性:文献［6］将蜂窝网络建模为Ginibre 点过程（Ginibre Point Process，GPP），并分析了平均干扰和覆盖概率；文献［7］捕获了基站中的非均匀性和耦合性，将其建模为泊松簇过程（Poisson Cluster Process，PCP），并推导出下行覆盖概率的精确表达式；泊松洞过程（Poisson Hole Process，PHP）模型用于拟合异构网络中基站位置的层间依赖性［8］。结果表明，非泊松点过程能更好地反映实际基站的空间分布特征。

能量效率作为HetNet 的关键性能指标，近年来引起了人们的广泛关注。文献［9］从最小能耗的角度给出了两层异构蜂窝网中各层基站的最佳密度；文献［10-11］研究了两层异构蜂窝网络下行链路的能量效率，提出利用波束成形和功率分配进行能效优化；文献［12-17］重点研究了K 层异构网的能效问 题，分 别 从 基 站（Base Station，BS）关 联 策 略［12］、BS 密度［13-15］、BS发射功率［16］和BS协作策略［17］等方面提出了能量效率的优化算法。然而，这些文献都在PPP 模型的基础上对网络的能量效率进行的研究。

MBS 的部署通常呈现一定的排斥性，非泊松点过程比PPP 更适合捕捉实际基站部署的空间特征。考虑到准确性、可操作性和实用性之间的权衡，本文将采用β-Ginibre 点过程（β-Ginibre Point Process，β-GPP）模型对宏基站进行建模。根据笔者的查询资料显示，基于非泊松过程的异构网络的能效分析和优化研究很少有报道。本文的主要工作如下:1）采用一种简单的近似方法分析了两层异构网络的信干比分布；2）推导了异构蜂窝网络的覆盖概率、平均可达吞吐量和系统的能量效率；3）提出了一种有效的能效优化算法，即寻找最优的微基站（Pico Base Station，PBS）发射功率，使能量效率最大化。

1 系统模型

本文考虑由宏基站（MBS）和微基站（PBS）构成的两层异构蜂窝网络:MBS 的部署采用β-Ginibre 点过程ΦM建模，其密度为λm；PBS 以齐次泊松点过程（Homogeneous Poisson Point Process，HPPP）ΦP分布的方式部署在宏小区范围内，其密度为λp。移动用户以密度为λu的独立HPPP ΦU分布在整个网络平面上。两层异构蜂窝网络模型如图1 所示。MBS 和PBS的发射功率分别用μm和μp表示。

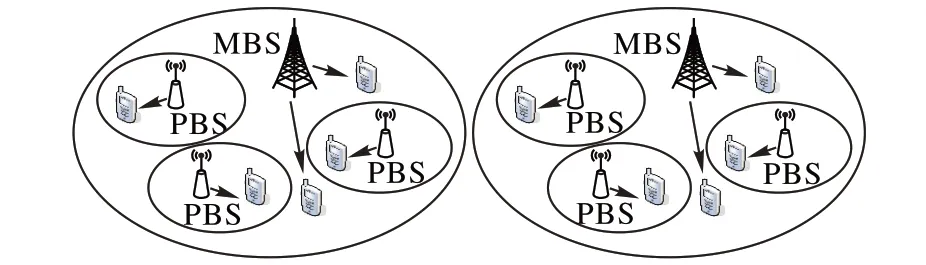
图1 两层异构蜂窝网络模型Fig.1 Two-tier heterogeneous cellular network model

由于网络模型的平稳性，所有用户都具有相同的统计特性，本文仅考虑位于原点的典型用户。假设典型用户与服务基站之间的距离为r，信道增益服从瑞利衰落，其均值为1，表示为h～exp(1)。以平均最大接收功率为接入BS 的准则，得到典型用户接入服务基站的接收功率为μxhr-α，其中路径衰耗因子α ＞2，μx表示基站x 的发射功率:当基站接入宏基站，x ∈ΦM，μx= μm；当基站接入微基站，x ∈ΦP，μx= μp。典型用户从异构网络中所有其他基站接收到的累积干扰功率用I 表示。在干扰受限的异构蜂窝网络中，噪声功率可以忽略不计。因此，可得典型用户在距离其接入基站随机距离r 处的信干比（Signal to Interference Ratio，SIR）表示为:

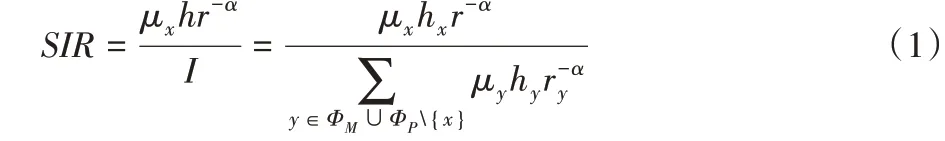
2 能量效率分析

2.1 覆盖概率

在干扰受限的异构蜂窝网络中，覆盖概率PC定义为发送端到接收端的信干比（Signal to Interference Ratio，SIR）大于或等于某个给定阈值θ 的概率，即PC= Pr(SIR ≥θ)。因为典型用户最多与某一层相关联，因此覆盖概率可以表示为两个不相交事件的总概率［18］，即

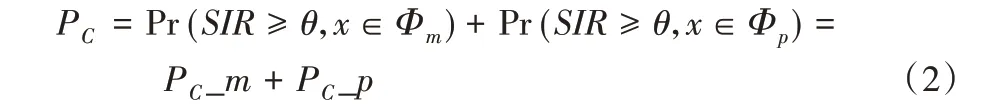
2.2 平均可达吞吐量

假设用τm和τp分别表示两层异构蜂窝网络中相关典型用户的平均遍历率。根据平均遍历率的定义，τm和τp可以表示为:

根据文献［24］中的定理2，基于MISR 的增益方法，平均遍历率τm和τp可以写为:

其中:

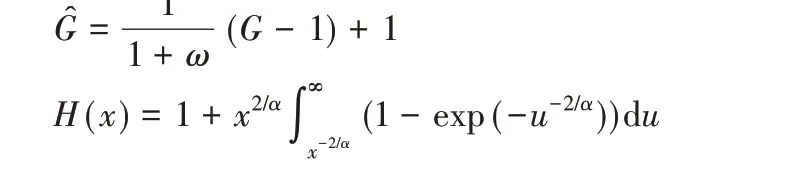
根据文献［25］中的引理1，典型用户接入宏基站的概率用Am表示:

在异构蜂窝网络中，宏基站和微基站所服务的用户数分别表示为Nm和Np。根据文献［25］，Nm和Np可以表示为:

平均遍历率τm和τp是指宏基站和微基站的平均吞吐量。根据异构蜂窝网络中每层基站服务的用户数，可以得到两层异构蜂窝网络的平均用户吞吐量为:

根据两层异构蜂窝网络的覆盖概率（式（4）～（5））、典型用户接入基站的概率（式（11）～（12））、两层网络的平均用户吞吐量（式（15）～（16））），可以得到整个异构网的平均可达吞吐量为:

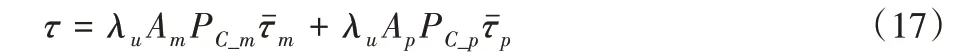
2.3 功率损耗

研究异构蜂窝网络的能效问题需要关注基站的功耗，即MBS和PBS的功耗，其功耗Pm和Pp可分别建模为:

其中:ξm和ξp为MBS 和PBS 的负载相关功耗系数，μm和μp为MBS 和PBS 的发射功率；Pm0和Pp0分别为MBS 和PBS 的静态功耗。由于ξm和ξp与MBS 和PBS 的流量负载成正比，而Nm和Np分别为MBS 和PBS 服务的用户数，所以可以用Nm和Np来替换ξm和ξp，这样每个MBS和PBS的功耗可以表示为:

因此，两层HetNet的总功耗可以写为

2.4 能量效率

能量效率定义为整个HetNet 的平均可达吞吐量与总功耗之比，表示为:

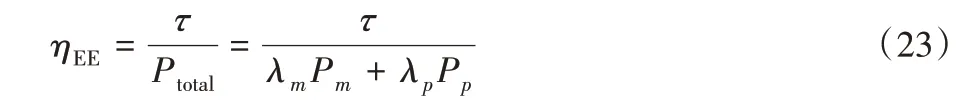
其中:τ为整个异构网的平均可达吞吐量。

3 能效优化

本文从基站发射功率的角度来优化能量效率。在HetNet中，宏基站通常用于基本覆盖，其传输功率一般不可调。因此，可以通过控制微基站的发射功率来优化能量效率。假设MBS的发射功率是一个固定值，优化问题可以表示为:

不难证明优化公式（23）的目标函数是凹函数。为了便于使用凸优化算法来解决这个问题，对式（23）取反，这样，优化问题式（24）就变成了一个凸优化问题。本文采用成功失败法来寻找优化问题的最优解。算法描述如下:

⑦反向搜索h=-0.25h，转到③。

在这里初始搜索步长h=0.1，计算精度ε=0.01，根据算法求得最优微基站发射功率x*0，即μ*p，把μ*p 代入式（23）即可得到能量效率的最大值。

4 仿真与结果分析

本章给出了两层HetNet 能量效率的仿真结果，仿真中所用到的相关参数的默认值如表1 所示。Ginibre 点过程（GPP）是一种带有排斥特性的点过程，属于行列式点过程的范畴；β-GPP 是 由GPP 经 过 稀 释 和 缩 放 后 得 到 的，0＜β ＜1，当β→0时，β-GPP弱收敛为相同密度的PPP［7］。在仿真中分析了基于PPP的网络和基于β-GPP的网络之间的性能比较。

表1 系统参数Tab. 1 System parameters

图2 给出了当λp= 2λm时，不同目标SIR 下，两层异构网的覆盖概率分布。从图2 可以看出，当β=1 时，β-GPP 网络覆盖概率的仿真结果与其相应的近似结果之间存在微小的差距。这个微小的差距可以归因于β-GPP 分布与PPP 分布之间的干扰近似。显然，在很大范围的SIR 内，覆盖概率的近似值是精确的，这验证了基于ASAPPP的方法的有效性。

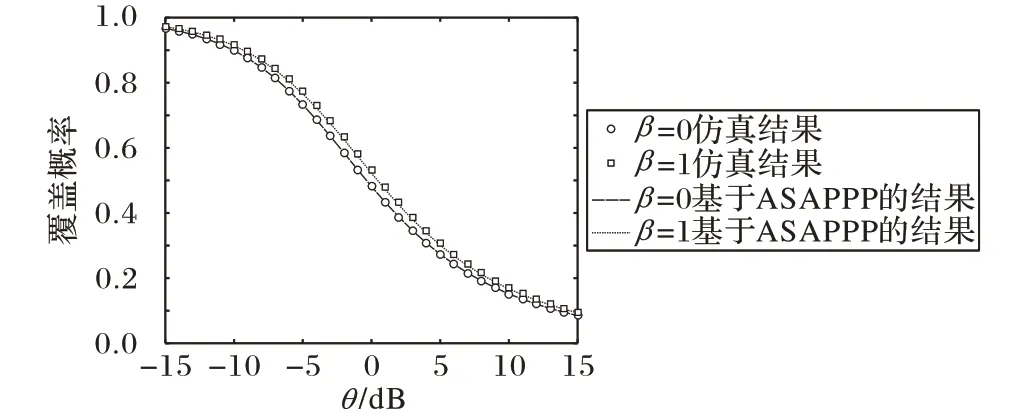
图2 覆盖概率与SIR的关系Fig. 2 Coverage probability versus SIR

图3给出了能量效率ηEE和PBS发射功率μp之间的关系。从图3 可以看出，能量效率先增大后减小，存在一个最优的发射功率使能量效率达到最高。图4描述了当λp= 2λm和λp=3λm时，两层蜂窝网络的能效与MBS 密度之间的关系。本文比较了两种情况下的能量效率:在一种情况下，PBS 的发射功率是固定的；在另一种情况下，PBS 的发射功率采用由能量效率优化算法获得的最佳发射功率。从图4 中可以看出，无论β = 0 还是β = 1，所提出的能量效率优化方案可以显着提高网络能量效率，尤其是在MBS 分布密度比较高的情况下。因此，通过为PBS 设置适当的发射功率，可以提高网络的能量效率。

5 结语

本文研究了PBS发射功率对两层HetNet能效的影响。首先基于SIR 分布的简单近似方法，推导出覆盖概率和平均遍历率，然后得到了两层HetNet 的能量效率。最后，提出了一种能量效率优化算法，以找出最佳的PBS 发射功率，提高HetNet 的能量效率。在仿真中，分析了PBS 发射功率对能量效率的影响，并验证了能量效率优化算法的有效性。本文的研究可为微基站的实际运行提供一定的理论参考。下一步将考虑微基站的密度与微基站发射功率的联合优化。

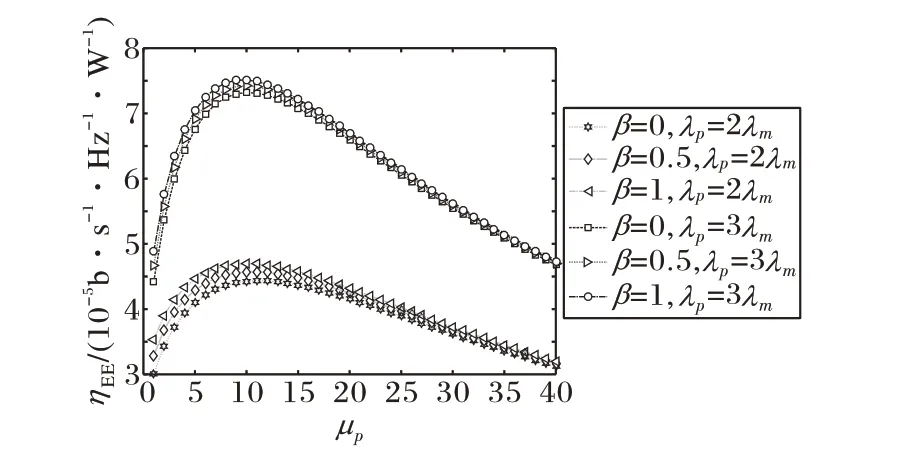
图3 能量效率ηEE与PBS发射功率μp的关系Fig. 3 Energy efficiency ηEE versus PBS transmitting power μp

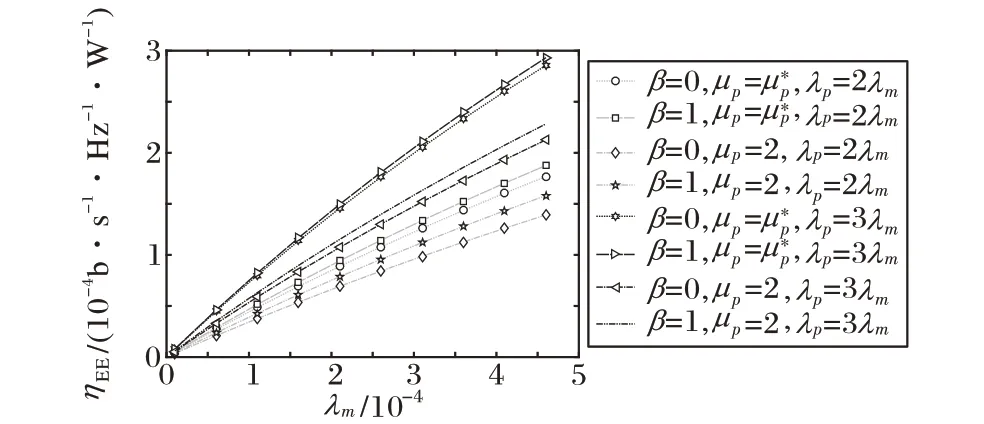
图4 能量效率ηEE与λm的关系Fig. 4 Energy efficiency ηEE versus MBS density λm