一类复杂通信条件下高阶线性群系统编队控制

石晓航，张庆杰，吕俊伟

（1.海军大连舰艇学院，大连116001； 2.空军航空大学，长春130022； 3.海军航空大学，烟台264001）

群系统编队控制在很多领域都有着广泛的应用，比如监视和侦察［1-3］、目标搜索和定位［4-7］、中继通信［8］以及空间探索和资源探测［9-10］等。传统的编队控制方法主要包括：领导者-跟随者［11-12］、行为方法［13］以及虚拟结构［14］。但从应用情况来看，这3种方法依然存在着鲁棒性差、行为建模复杂和通信量大等方面的不足。随着多智能体一致性理论的发展，越来越多的学者开始研究基于一致性算法的分布式编队控制方法［15-16］。文献［15］指出，上述3种传统方法均可看作是一致性算法的特例。

基于一致性协议，文献［17-18］讨论了轮式小车的编队控制问题。文献［19］提出了大规模一阶群系统有限时间编队框架。基于一致性线性化反馈方法，文献［20］研究了无领导者方式的多无人机编队控制问题。进一步，文献［21］研究了多无人机时变编队控制的分析和设计问题，并给出了编队形成的充要条件。文献［15，17-21］的研究对象 主 要 是 低 阶 群 系 统，比 如 一 阶［17-19］、二阶［15，20-21］。假 定 网 络 通 信 拓 扑 为 无 向 图，文献［22］分析了一类由多个二阶系统串联组成的高阶群系统编队控制问题。对于有向通信拓扑结构，由于其Lap lacian矩阵的特征值可能存在复数，判断编队形成具有一定难度。文献［23］利用状态／输出反馈，研究了有向通信拓扑条件下的编队形成问题。

上述文献均假设理想网络通信条件，但在实际的应用中，受到周围环境或其他因素的影响，可能出现通信时延、拓扑不确定以及外部扰动等情况。文献［24］通过引入自身时延，给出了二阶群系统实现时不变／时变编队的充分条件。文献［25］讨论了同时存在位置时延和速度时延条件下的一致性策略和编队控制稳定性。文献［26］采用频域方法，借助Nyquist稳定性判据给出了编队稳定的时延相关／非相关条件。文献［24-26］均假定固定通信时延。对于时变时延，文献［27］研究了某型垂直起降无人机的编队控制方法。同时考虑时变时延和有向拓扑，文献［28］设计了二阶群系统编队控制协议，同时讨论了时变时延对编队形成的影响。文献［29］给出了含有时变时延高阶群系统实现编队的充要条件和编队控制器的设计方法。文献［30-31］采用Lyapunov稳定性理论分析了通信时延的边界条件。文献［32-33］研究了群系统模型存在范数有界不确定性情况下的编队控制问题。利用鲁棒控制理论，得到了群系统编队控制稳定性条件。针对时延、拓扑不确定和外部扰动条件下的高阶群系统编队控制问题，目前的研究成果很少。文献［34-35］只讨论了控制器增益已知情况下的群系统鲁棒一致性问题。

本文主要讨论一类同时存在时变时延、拓扑不确定和外部扰动等复杂通信条件下的群系统编队控制问题。与已有文献相比，主要贡献有：

1）高阶线性群系统模型。文献［17-21］所讨论的群系统大都针对一阶或二阶积分器，而高阶模型不具有一阶、二阶模型的特殊结构，因此文献［17-21］方法不适于高阶线性群系统。本文方法具有更广泛的应用范围。

2）同时考虑时变时延、拓扑不确定及外部扰动等3种通信条件。目前针对复杂通信条件的编队控制问题研究较少，仅有文献［34-35］讨论了3种通信条件同时存在的群系统一致性可行性问题，且没有给出控制器增益的求解方法。

3）低保守性。文献在分析编队所允许的最大时延上界时采用了Lyapunov稳定性方法，所得结果是充分条件，具有一定的保守性。不同于文献［30-31］方法，本文将自由权矩阵引入分析过程中，使所得结果具有较低的保守性。

本文首先简要介绍了图论知识和相关引理；并建立了一类复杂通信条件下高阶线性群系统编队问题的数学描述，同时设计了基于一致性算法的编队控制协议。然后给出了群系统实现编队的充要条件，利用Lyapunov-Krasovskii泛函分析方法得到群系统编队所允许的最大时延上界和控制器增益求解方法。最后利用数值仿真实验，对所提出方法的有效性进行验证。

1 图论知识及相关引理

1.1 图论知识

1.2 相关引理

引理1［36］图G的Laplacian矩阵L至少有一个0特征值，且向量1是0特征值所对应的右特征向量，即L1＝0。如果图G是一个有向图，且含有一个有向生成树（至少存在一个节点到其他所有节点都有一条有向路径），则0是L的单特征值，其余的非零特征值均具有正实部。

引理2［37］如果矩阵Y∈RN×N的各行和均为 零，则 存 在 矩 阵 Z∈RN×（N－1）和 矩 阵 E∈R（N－1）×N使得Y＝ZE，E的定义为

如果0是矩阵Y的单特征值，那么矩阵Z是列满秩的。

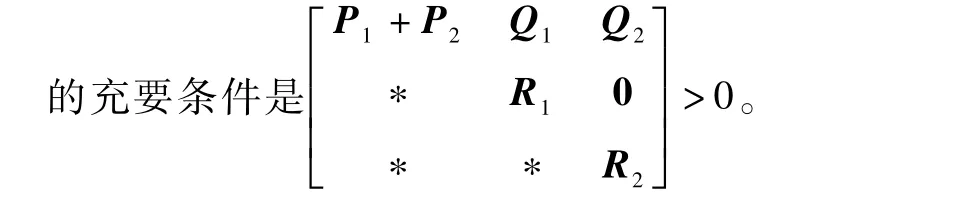
引理5［40］给定具有适当维数的矩阵Q ＝QT、H和E，则Q＋HF（t）E＋ETFT（t）HT＜0，对所有满足FT（t）F（t）≤I都成立的充要条件是存在一正数ε＞0使得Q ＋ε－1HHT＋εETE ＜0成立。

引理6［41］对矩阵X∈Rm×n和矩阵Y∈Rn×m（n≥m），二者乘积满足如下性质：①若λ是矩阵XY的特征值，则λ也是矩阵YX的特征值。②若λ≠0是矩阵YX的特征值，则λ也是矩阵XY的特征值。③若λ1，λ2，…，λm是矩阵XY的特征值，则矩阵YX的n个特征值为λ1，λ2，…，λm，0，…，0。

2 问题描述

2.1 高阶线性群系统模型

2.2 编队控制协议

3 主要结果

3.1 编队形成的充要条件

针对高阶线性群系统的编队形成问题，本文主要考虑如下3种通信约束。

假设1 时变时延dt满足：

式中：¯dt和μ为常数，且0＜μ＜1。

假设2 拓扑不确定性。若用邻接矩阵的变化量ΔW ＝［Δwij］∈RN×N来描述通信拓扑不确定性，则有

式中：矩阵E的定义由引理2给出。

由引理1、引理2可知，存在列满秩矩阵Z∈RN×（N－1）及ΔZ∈RN×（N－1），使 得L＝ZE，ΔL＝ΔZE，对式（12）求导得到

考虑J和ΔJ的结构，闭环系统（16）等价于定理1的条件3中的N－1个闭环子系统，其中λi（i＝1，2，…，N－1）表示矩阵EZ的特征值，由引理1和引理6可知，矩阵EZ的特征值与矩阵L的非零特征值相同，因此λi（i＝1，2，…，N－1）也是矩阵L的N－1个非零特征值。由上述推导可知条件3也是必要的。

充分性 因为矩阵B是列满秩矩阵，由引言可知，存在一个非奇异矩阵～B＝［～BT1，～BT2］T，满足～B1B＝I且～B2B＝0。

如果条件1和条件2成立，则有

3.2 K2的设计

定理2 考虑复杂条件（4）、（5）和（6），若存在适当维数的实矩阵¯P＝¯PT＞0，¯Q＝¯QT≥0，¯R＝¯RT＞0，¯V以及常数a和b（b≠0），ε＞0，使得下式成立：

接下来将分别讨论ϖ⌒（t）≠0和ϖ⌒（t）＝0两种情况。

由引理4可知，式（27）与式（28）同时成立，当且仅当

根据引理3，式（30）等价于

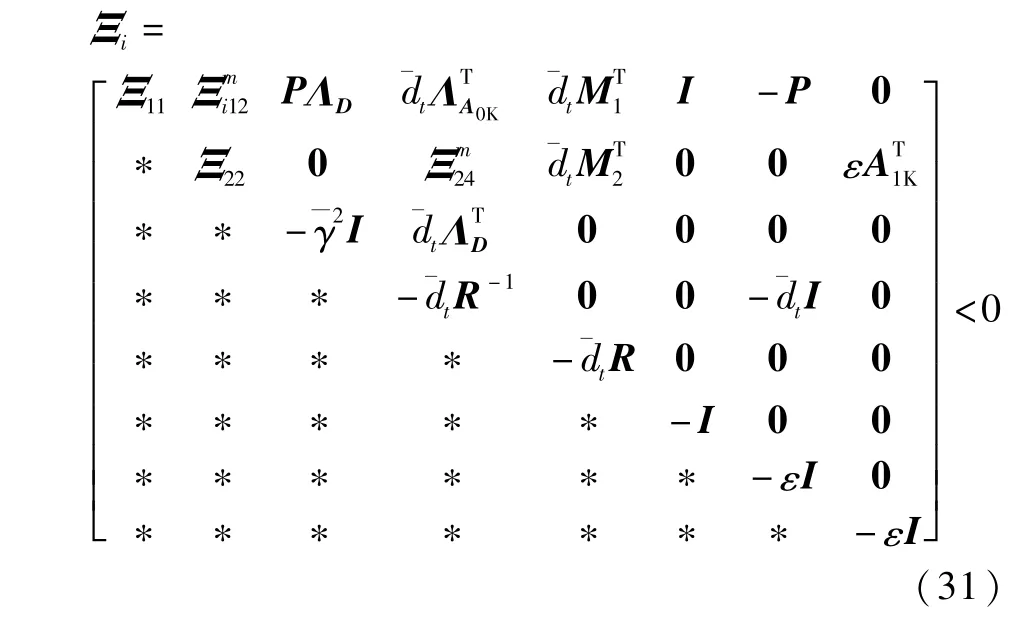
通过上述整理可知，如果不等式（31）成立，则不等式（26）成立，即闭环系统（10）在非零的ϖi（t）扰动条件下，具有给定的H∞性能指标γ。

基于上述的讨论，可以利用如下的算法对编队控制协议（2）进行设计，使群系统（1）在时变时延、通信拓扑不确定和外部扰动条件下，满足给定的H∞性能指标。

算法1 对于群系统（1）和编队控制协议（2），控制器增益K1和K2，以及辅助函数vi（t）（i＝1，2，…，N）的设计可以参照如下步骤：

步骤1 判断定理1的条件1中式（8）是否成立，若成立，则通过条件2的式（9）求解出编队辅助函数vi（t）。

步骤2 选取适当的控制器增益K1，令A＋BK1的特征值在复平面上的指定位置，完成对编队中心运动模态c（t）的配置。

步骤3 根据定理2，可以求出a、b和时延上界¯dt，进而得到控制器增益K2。同时，利用参数a和b，还可以得到不同时延下对应的控制器增益K2。

4 数值仿真

假设1个群系统由8个主体组成，各个主体之间的通信拓扑G如图1所示。

图1 通信拓扑GFig.1 Communication topology G

形成编队之后，8个主体会分布在一个椭圆形的圆周上，组成一个八边形并围绕椭圆的圆心旋转。

利用算法1中的步骤1，可以求解出编队辅助函数为

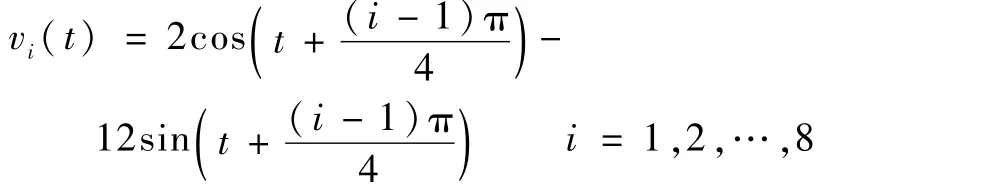
选取K1＝［5.75，－8.5，－8］将A＋BK1的极点配置在－2、－1＋i和－1－i。这时，编队参考c（t）是静止的。设定γ＝1.4，利用算法步骤3，得到时变时延上界为¯dt＝1.7 s。选取时变时延为dt＝1.2＋0.5sin t s，此时，得到的控制器增益为

K2＝［－0.016 4，0.0141，0.0084］。

各主体的初始状态分别为：xi1（0）＝4（δ－0.5），

xi2（0）＝3（δ－0.5），xi3（0）＝2（δ－0.5）（i＝1，

2，…，8），其中δ为（0，1）之间的随机数。通信拓扑的不确定性为ΔL＝0.9sin t L，外部扰动ωi（t）取［－2，2］之间的随机数。仿真时间为50 s，假设通信拓扑的不确定性始终存在，并在25～27 s加入外部扰动。图2（a）～（f）给出了8个主体的状态和c（t）的状态在不同时刻的截图，以及8个主体的编队构型。从图中可以看出，本文设计的编队控制协议可以使群系统在具有时变时延、通信拓扑不确定和外部扰动的条件下形成时变编队。在出现外部扰动时，8个主体的队形受到了一定的影响，但扰动消失之后仍能重新形成指定的时变编队并保持稳定。图3（a）～（c）分别给出了各主体的3个状态与编队相应状态差值的曲线，各主体3个状态与参考编队相应状态分量的差值曲线逐渐减小并趋于一致，在外部扰动出现之后，各主体的误差一致性受到了一定的影响，但各主体能迅速地调整各自状态并恢复指定的编队。从仿真结果可以看出，本文的控制方法具有抗扰动的性能，可以有效地抑制时变时延、通信拓扑不确定及外部扰动对群系统编队形成产生的影响，能保证群系统形成时变编队并保持队形稳定。

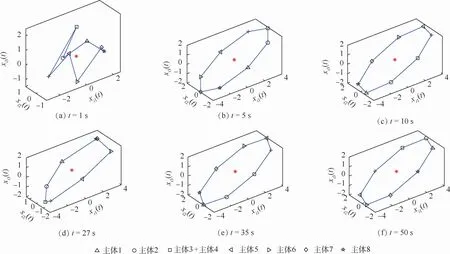
图2 8个主体的状态和c（t）的状态在不同时刻的截图Fig.2 Snapshot of states of eight agents and c（t）at differentmoments

图3 主体与编队的状态差值曲线Fig.3 State curves of differences between agents and formation

图4 8个主体的性能指标曲线Fig.4 Performance index curves of eight agents

5 结 论

本文讨论存在时变时延、通信拓扑不确定和外部扰动的高阶线性群系统编队控制问题，具体结论如下：

1）给出了群系统在给定的H∞性能指标下，实现编队H∞控制的充要条件。

2）采用变量代换，将群系统的编队控制问题，转化为具有外部扰动时延系统的H∞控制问题。通过构造公共Lyapunov-Krasovskii泛函，讨论了具有外部扰动时延系统的H∞控制问题，得到了保守性较小的LMI判据，利用数值计算方法，可得到群系统允许的时延上界。