乏燃料棒中关键核素径向分布特点及对废包壳测量准确度影响

柏 磊，王仲奇，刘晓琳，何丽霞，夏兆东，吕 牛

(中国原子能科学研究院，北京 102413)

基于我国核工业遵循的闭式循环发展路线，从反应堆卸出的乏燃料需通过后处理提取其中的U、Pu核素，经加工制成核燃料后进入再循环。目前采取水法后处理工艺，乏燃料组件经剪切、溶解、浸取后剩余的固态部分称为废包壳[1]，其中含有剪断的燃料包壳和未完全溶解的乏燃料。因废包壳中含有超U产物和裂变产物核素，具有很强的放射性，根据核材料管制、工艺控制和废物处理处置的要求[2]，需测定废包壳中的U、Pu含量。考虑到被测对象的复杂性，通常采用非破坏性测量方法(nondestructive assay, NDA)结合燃耗、堆功率、冷却时间等参数测量分析废包壳中的U、Pu及α核素含量(浓度)。

废包壳中关键核素测量分析非常复杂，影响测量结果不确定性的源项众多，仅空间分布就非常复杂。理想状况下，废包壳由大量空心的长3～5 cm的包壳管随机填充而成，这种不均匀分布会给测量分析结果引入相应的不确定度[3]。乏燃料剪切和溶解过程的随机性也会引入不确定度。然而，更重要的系统误差源项则是来源于乏燃料芯块中燃耗的径向非均匀分布。作为测量分析的重要输入参数，燃耗是堆内235U平均消耗的数量体现，由于反应堆运行过程中堆内中子注量分布的非均匀性，必然导致乏燃料元件芯块的内部燃耗和其中的关键核素质量组成的空间分布的不均匀。这种差异是废包壳测量分析结果误差的重要来源之一。本文开展乏燃料芯块中关键核素径向非均匀分布特性的研究，并分析其对废包壳测量结果的影响。

1 废包壳测量分析方法

通过直接测量废包壳中U、Pu的特征γ射线或中子发射信息来推导其含量非常困难，主要原因是废包壳中含有大量的超U核素和裂变产物核素，如锔、镅、铯和铕等，这些干扰核素的发射信息强度过大，导致U和Pu的发射信息被掩盖。因此废包壳测量中常采用间接的方式进行测量分析。常用的废包壳NDA测量方法有被动中子测量方法和被动γ测量方法[4]，这两种分析技术的测量原理和技术参数列于表1[5-7]。

表1 常规废包壳NDA测量方法Table 1 Common NDA measurement method of leached hull

表1中，直接测量核素指通过测量废包壳发射的中子和(或)特征γ射线，结合系统效率刻度数据和此核素的放射性基本数据，可直接分析得到质量的核素；核素质量比是采用模拟计算或其他技术间接得到废包壳中其他感兴趣核素的质量比。通过这两组数据即可求解废包壳中含有的核材料U和Pu的质量，其计算公式为：

(1)

式中：MU(Pu)为核材料U和Pu的质量；Cpi为测量得到的中子或某特征γ射线扣除测量本底之后的净计数率；εi为系统效率刻度系数；Cpi/εi为表1中直接测量核素的质量，即mi；N为单位质量直接测量核素的特征信号的发射率；MU(Pu)/mi为表1中废包壳中的核素质量比，通常为计算值。

该公式的前提条件是，假设废包壳中关键核素的质量比与对应的未剪切前乏燃料组件中相同，乏燃料组件内的关键核素质量组成信息是采用核电站运行数据的堆功率、燃耗、冷却时间等参数计算得到。根据PUREX乏燃料后处理工艺特点，废包壳中残留的乏燃料约占0.1%～1%，通常表现为紧附在燃料包壳内壁上的薄层，因此，废包壳中残留物中关键核素的质量(活度)比与乏燃料整体的质量(活度)平均比之间可能存在的差异，将在很大程度上决定了废包壳测量分析结果的准确性。

2 乏燃料元件棒中关键核素的径向分布不均匀原理与计算模型

核电站堆内的热中子和超热中子在燃料芯块中的平均自由程较芯块的直径小得多，由于大部分的热中子和超热中子来自于元件棒的外部，所以其中的大部分在芯块的外部区域被吸收了，芯块的边缘区域(Rim区域)会因为这种共振吸收反应而受特别影响。因此，芯块中心的中子注量会显著低于芯块径向边缘处的中子注量，而芯块中的径向功率曲线与中子的径向注量分布相似，因此在辐照期间，芯块燃耗径向分布将会不均匀，而且径向上也明显在芯块的边缘存在1个峰值[8]。乏燃料元件芯块中的Pu浓度在外围区域会急剧增大[9]。

夏兆东等以日本原子能机构公开发表的Takahama-3核电站乏燃料成分为基准，采用相同计算配置，应用蒙特卡罗模拟计算程序，开展了计算模型的比对研究[10]。

在此基础上，选用上述模型计算了国内核电站运行的AFA-3G组件中的元件棒在不同燃耗情况下的关键核素随芯块半径的分布特性。计算时，将每个元件棒沿半径从内到外划分为11个环，半径比(r/r0，其中r为分环的外径，r0为燃料芯块半径，取4.096 cm)分别为0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.995、0.999 5、1，其中最外两环的内径按体积比分别占1/100和1/1 000计算而来。燃料棒分环如图1所示。

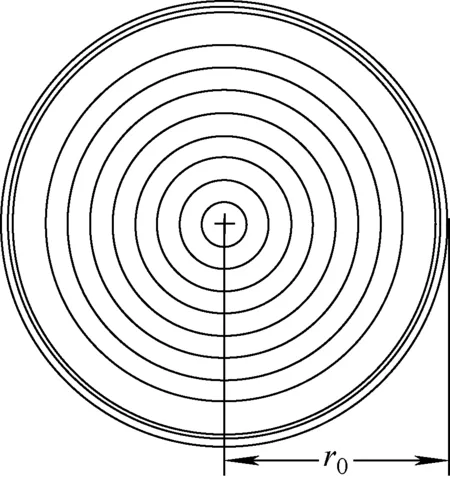
图1 燃料棒分环示意图Fig.1 Ring diagram of fuel rod

3 关键核素浓度径向分布特性研究

根据表1，测量废包壳主要关注235U、137Cs、154Eu、106Ru、144Ce、244Cm和U、Pu含量。在此基础上，选用上述模型计算了国内运行的AFA-3G组件在不同燃耗、不同冷却时间情况下的关键核素随芯块半径的分布特性。

由于235U的平均消耗与乏燃料的燃耗呈正比，故可通过芯块径向各层235U浓度变化来展示燃耗的径向变化趋势。表2列出了平均燃耗15～65 GW·d/t(U)范围内(冷却时间为5 a，余同)径向各层内的235U浓度。

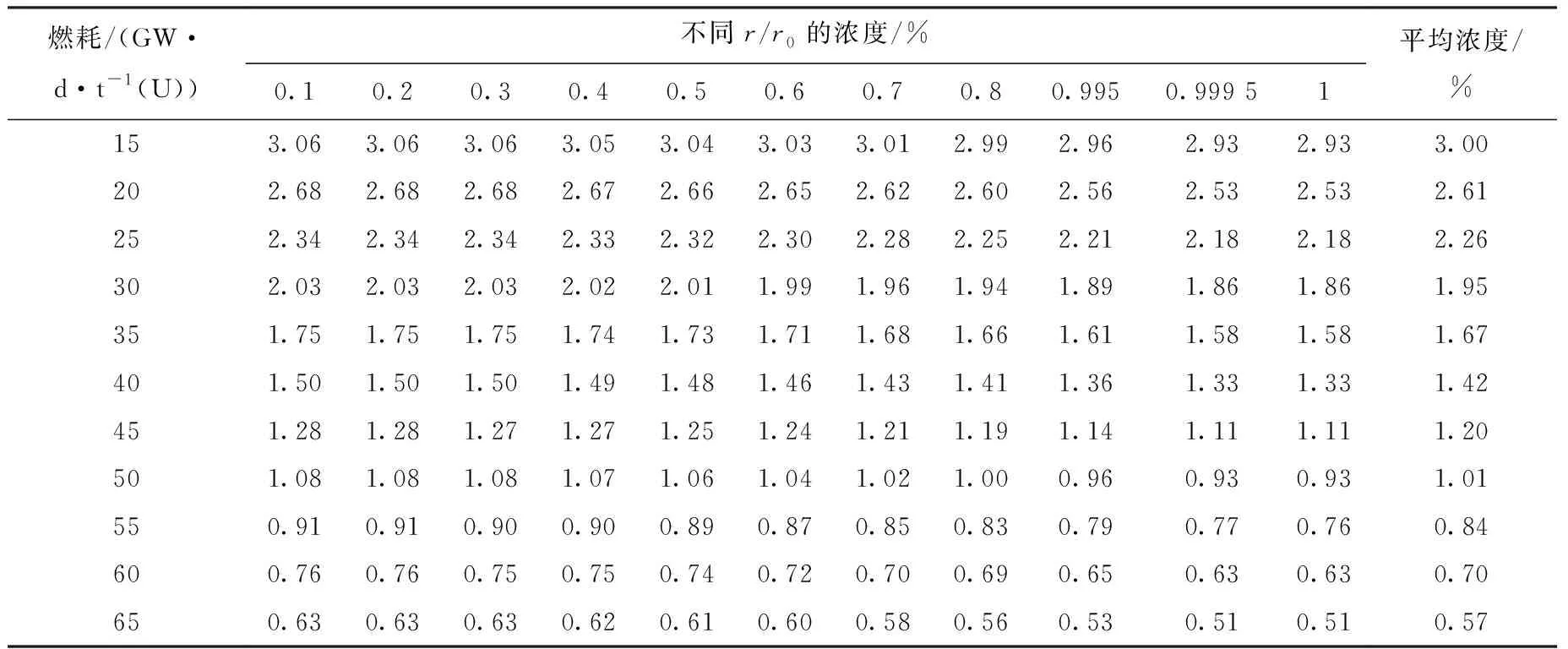
表2 不同燃耗情况下的235U浓度径向分布Table 2 235U concentration distribution along radius in each ring with different burnups

由表2可看出，不同燃耗乏燃料中235U浓度随半径的增大而逐渐减小，这也说明了燃耗随径向分布逐步提高，尤其是最外部两层(分别代表了残留1%和残留0.1%)，下降趋势急剧增大，这与分环燃耗随分环半径的增大而增大一致。随整体燃耗的增加，Rim区域(最外两层区域)的235U浓度与平均浓度之间相对偏差甚至可达10%之上，数据分布示于图2。

表2中，r/r0为0.999 5和1时235U浓度基本相等，原因在于该r/r0逼近于1，量化差异相对于热中子在燃料中的平均自由程来说几乎可忽略，故发生反应的概率相当，因此235U损耗量近似相等。

表1中被动γ测量方法主要是测量废包壳中残留的裂变产物，综合考虑裂变产额、乏燃料冷却时间、特征γ射线能量、分支比等信息，通常选择137Cs、154Eu、106Ru和144Ce 4种核素中的1种作为测量分析对象。被动中子测量方法则主要关注热中子的主要贡献体，根据文献[4]，冷却时间5 a以上的乏燃料组件中，绝大部分的自发中子来自于244Cm，通常占比97%以上。

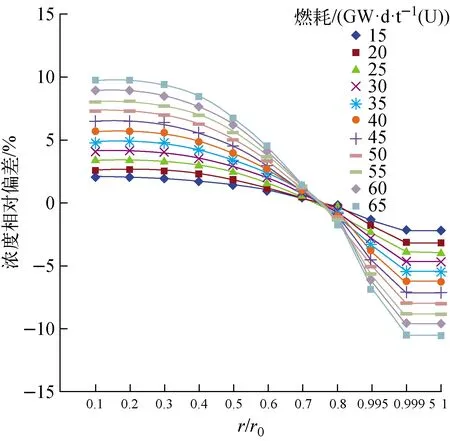
图2 不同燃耗235U浓度相对偏差的径向趋势Fig.2 Radial distribution of relative deviation of 235U concentration with different burnups

根据建立的计算模型，此5种关键核素在不同燃耗情况下质量浓度相对偏差的径向分布如图3所示。

由图3可看出，各层由内至外质量浓度相对平均值的偏差逐步加大，尤其是关注的最外层，137Cs、154Eu、106Ru、144Ce和244Cm的相对偏差分别约34.78%、39.45%、64.57%、38%和100.58%。且同235U浓度变化趋势类似，在Rim区域此5种关键核素浓度剧烈提升，最外层两环之间浓度相对也有少量提升。同时，这种浓度的偏差也随燃耗的提升而变大，尤其是在Rim区域。但值得注意的是，244Cm的相对偏差随燃耗变化趋势极小，几乎可视为与燃耗无关。

而废包壳测量的最终关注点是其中所有U和Pu核素的含量，图4为总U和总Pu质量浓度的径向相对偏差变化趋势。

由图4可看出，各层由内至外总U质量浓度相对偏差逐步降低，且随着燃耗加深，这种差异更明显，但其最外层最大相对偏差仅-3.34%，这主要是由于占主导地位的238U变化不大导致。而总Pu质量浓度相对偏差的径向变化趋势则与图3中5种核素类似，其最大相对偏差达64.25%。但与上述各核素均不同的是，各层相对偏差随燃耗升高而降低，最外层和最内层之间的质量浓度差异也降低，这说明，随着平均燃耗的提升，各层之间燃耗变化趋势变缓。

图4 不同燃耗下总U(Pu)浓度相对偏差的径向趋势Fig.4 Radial distribution of relative deviation of total U(Pu) concentration with different burnups

4 径向特性对废包壳测量影响修正研究

根据式(1)，获取废包壳中总U和总Pu的质量，需重点关注MU(Pu)/mi。结合各关键核素径向分布数据，可获得该比值的径向分布。图5示出137Cs、154Eu、106Ru、144Ce、244Cm与待分析Pu总量的质量比趋势。径向各层U浓度变化见图4a，其变化趋势相对较小，则U总量趋于一常数，各关键核素与U总量的比值变化趋势与各核素浓度径向分布类似，见图3。

随着燃耗加深，137Cs和总Pu的含量均在增大，但从径向分层上看，其137Cs/Pu质量比随燃耗加深相对偏差平均值反而降低。154Eu/Pu质量比和144Ce/Pu质量比的趋势与137Cs/Pu质量比的相似，但106Ru/Pu质量比的则不同，其原因主要是由于各种裂变核素随燃耗的产额变化不同导致。

从图5可看出，芯块径向边缘处的核素质量比与芯块整体的核素质量比平均值之间存在显著差异，大多数残留物存在于芯块最边缘的两环内，因此采用式(1)计算U、Pu质量时，引用燃料组件的平均燃耗会产生较大不确定度。为减小这种径向差异给分析结果带来的影响，考虑在式(1)中乘以修正因子K。以被动γ测量方法为例，假设通过模拟计算可得到整体的244Cm/U质量比和244Cm/Pu质量比为R0；而当残留比例为0.1%时，即仅残留了最外层(图1)，则残留物中实际的244Cm/U和244Cm/Pu质量比为R1(式(1)中的核素质量比)，即K=R1/R0。

根据模拟计算结果，则可得到不同燃耗、冷却时间的K。表3列出了冷却5 a的情况下不同燃耗的K，其他冷却时间的情况可类推。

根据表3，采用二次多项式拟合方式，则可给出修正因子K与燃耗(x)之间的拟合公式(表4)。

图5 不同燃耗下关键核素与总Pu质量比相对偏差的径向趋势Fig.5 Radial distribution of relative deviation of mass ratio of key nuclides to total Pu with different burnups

表3 不同燃耗下的K
Table 3Kwith different burnups

核素质量比不同燃耗(GW·d·t-1(U))下的K1520253035404550556065137Cs/Pu-28.67-26.62-24.58-22.56-20.62-18.61-17.16-14.79-12.99-11.24-9.50154Eu/Pu-25.15-23.04-21.01-19.11-17.22-15.34-13.90-11.56-9.78-8.03-6.37106Ru/Pu-9.35-5.78-2.88-0.351.793.804.977.098.399.5010.50144Ce/Pu-30.26-28.25-26.11-23.87-21.58-19.22-17.23-14.34-11.97-9.61-7.34244Cm/Pu19.8821.5023.2024.8126.3927.8528.5630.5431.7332.8233.81137Cs/U18.0020.6823.2025.6127.9230.0832.1034.0935.9037.6939.44154Eu/U23.8126.5729.0331.2233.3935.3237.3039.1740.9042.6844.27106Ru/U49.9654.9558.6561.6564.0265.9267.4068.5369.2869.8670.26144Ce/U15.3718.0120.7223.5026.3629.1231.9934.8037.4840.2242.77244Cm/U98.3299.83101.26102.47103.67104.34105.02105.43105.74106.05106.18

表4 K与燃耗关系拟合公式Table 4 Fitting formula of K and burnup

续表4

5 总结

本文利用分环模式建立的乏燃料元件棒计算模型，给出了乏燃料元件棒内关键放射性核素质量浓度随半径、燃耗的变化。结果表明，此燃料元件棒各环燃耗水平从轴心沿径向逐步提高，尤其是最外层的边缘区域，提升尤其显著，从而导致废包壳中关键核素浓度相对燃料元件棒平均值显著变化。同时根据后处理工艺中废包壳中残留物的物理分布特点，结合常用废包壳测量分析方法，给出了修正因子以修正因径向分布不均匀带来的误差。

而在后处理工程应用中，常作为输入信息的是组件的整体平均燃耗，此时不仅组件内不同元件棒的平均燃耗有差异，即使对于同一根元件棒，轴向上的燃耗也不均匀。基于单根元件棒径向平均燃耗与残留物燃耗之间的差异研究数据，可结合上述两种不均匀分布情况，开展进一步的研究工作，提高废包壳测量系统的工程应用水平。