液态熔盐堆堆芯功率内模控制器设计与仿真
曾文杰,朱伟聪,谢金森,姜庆丰,于 涛
(南华大学 核科学技术学院,湖南 衡阳 421001)
内模控制具有响应速度快、抗干扰能力强、结构简单和成本低等优点,目前内模控制已广泛用于电气工程、火电厂、电子通信等领域[1-3]。液态熔盐堆一回路系统是一个非线性的复杂系统,设计一个性能良好的堆芯功率控制器对实现一回路系统的稳定运行至关重要[4]。
为研究液态熔盐堆堆芯功率控制,本文采用集总参数法建立熔盐实验堆一回路非线性模型[5],并采用微扰理论对非线性模型进行线性化处理,建立系统线性化模型。在此基础上,根据内模控制理论[6-9],设计液态熔盐堆堆芯功率内模控制器[9-15],以熔盐实验堆MSRE为对象进行控制器仿真分析。
1 液态熔盐堆一回路模型
由于液态熔盐堆堆芯燃料具有流动性,堆芯出口处燃料温度经过时间延迟后作为热交换器一次侧入口温度,热交换器一次侧出口温度经过时间延迟后作为堆芯进口处燃料温度,从而可更准确地模拟系统温度在瞬态过程中的变化。采用集总参数法建立系统非线性模型。
1.1 堆芯动态模型
1) 堆芯物理模型
基于点堆动力学模型,根据中子密度与缓发中子先驱核密度守恒原理,建立堆芯物理模型[5]:
(1)
(2)
(3)
(4)
(5)
(6)
式中:P为反应堆功率;ci为第i组缓发中子先驱核密度;t为时间;ρ为引入堆芯的总反应性;β为缓发中子总份额;βi为第i组缓发中子份额;λi为第i组缓发中子先驱核衰变常量;Λ为堆内中子代时间;τc、τl分别为熔盐燃料在堆内的流动时间和堆外的流动时间。
对式(1)、(2)进行归一化处理得:
(7)
(8)
式中:Pr为相对功率,Pr=P/P0,P0为堆芯初始稳态功率;cir为第i组缓发中子先驱核相对密度,cir=ci/ci0,ci0为堆芯初始稳态先驱核浓度。
2) 堆芯热工模型
基于堆芯燃料和石墨的能量守恒,假设堆芯燃料和石墨的物性参数为常数,系统的流动为不可压缩流动,建立堆芯热工模型[5]:
(9)
(10)
(11)
式中:Ts为堆芯燃料平均温度;Tg为石墨平均温度;Tsi为堆芯进口处燃料温度;Tso为堆芯出口处燃料温度;γs、γg分别为燃料产热总份额和石墨产热总份额;Ms为燃料质量;cps为燃料比定压热容;Mg为石墨质量;cpg为石墨比定压热容;U为燃料和冷却剂间的换热系数;Гs为燃料质量流量。
3) 堆芯反应性模型
液态熔盐堆的反应性平衡方程[5]为:
ρ=ρ0+αrodΔz+αs(Ts-Ts(0))+
αg(Tg-Tg(0))
(12)
(13)
式中:ρ0为初始反应性;αrod为控制棒反馈系数;Δz为控制棒棒位变化;αs、αg分别为燃料熔盐温度反馈系数和石墨温度反馈系数;Ts(0)、Tg(0)分别为稳态时刻堆芯燃料熔盐平均温度和堆芯石墨平均温度。
1.2 热交换器动态模型
为方便建立热交换器动态模型[5],假设热交换器两侧流体均为单相流动,且热流介质的物性参数为常数。经简化处理后,将热交换器的换热通道简化为一次侧、管壁和二次侧组成的流体沿壁面两侧逆流换热的模型[5]:
(14)
(15)
(16)
(17)
式中:MHe,s、MHe,c分别为热交换器一次侧和二次侧熔盐质量;cs、cc分别为热交换器的一次侧和二次侧熔盐热容;Usc为热交换器一次侧与二次侧间的热传导系数;Гs、Гc分别为流经热交换器一次侧和二次侧质量流量;THe,s、THe,c分别为热交换器一次侧和二次侧熔盐平均温度;THe,so、THe,co分别为一次侧和二次侧出口温度;THe,si、THe,ci分别为一次侧和二次侧进口温度。
1.3 延时环节
在液态熔盐堆中,堆芯与热交换器之间均存在着管道延时。将管道延时表示成如下形式[5]:
THe,si(t)=Tso(t-τ1)
(18)
Tsi(t)=THe,so(t-τ2)
(19)
1.4 线性化模型
依据微扰理论,在式(1)~(19)的基础上分别建立堆芯和换热器的线性状态空间模型:
(20)
(21)

(22)
(23)
Bc=
(24)
(25)
(26)
由式(14)~(17),建立换热器状态空间模型:
(27)
(28)
(29)
(30)
(31)
(32)
(33)
(34)
式中,δ为微小扰动。
2 仿真系统开发与应用
2.1 堆芯功率内模控制器设计
1) 内模控制原理
内模控制[6]的一般结构如图1所示。内模控制设计思路是将对象模型与实际对象相关联,控制器逼近模型的动态的逆,故其是一种基于模型逆的控制方法。对单变量系统而言,内模控制器取模型最小相位部分的逆,并通过附加低通滤波器以增强系统的鲁棒性。理想内模控制器存在以下问题[7]:若模型存在非最小相位相,则内模控制器取Q(s)=M-1(s)时存在超前项,在物理上无法实现;当M(s)严格正则时,理想控制器则非正则,从而导致此控制器微分环节对干扰异常敏感。为解决此问题,一般采用两步法[7]。

图1 内模控制原理框图Fig.1 Block diagram of internal model control
两步法设计内模控制器基本思路如下。

(2) 引入低通滤波器。由于一般情况下控制对象G(s)稳定,为保证内模控制器Q(s)的可实现性及稳定性,引入一个低通滤波器F(s)与内部模型M(s)的逆相乘得到控制器模型[7]如式(35)所示。
(35)
(36)
式(36)中,λ为控制器设计的唯一可调参数,决定着系统的响应速度和鲁棒性。随着λ的增加,系统的鲁棒性能提升,但跟踪性能将变差,因此,λ的选取需对系统的跟踪性能和鲁棒性进行折中考虑,此处根据实际仿真结果筛选最佳λ=3。
2) 内模控制器数学模型的获取
在控制系统的辨识过程中,通常情况下采用开环系统辨识法[7]辨识得到内部模型M(s)。利用工业上常用的一阶惯性加滞后模型FOPDT(first order plus dead time model)[7]系统表示,系统的传递函数M(s)如式(37)所示。
(37)
式中:Kp、Tp、θ为待辨识参数;m为内部模型的阶数。对式(37)左右两侧取自然对数后,进行两次求导得到下式:
(38)
(39)

(40)
(41)
Kp=(Tpa+1)G(a)eaθ
(42)
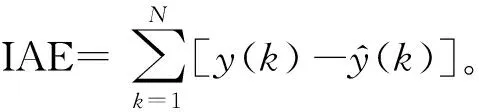
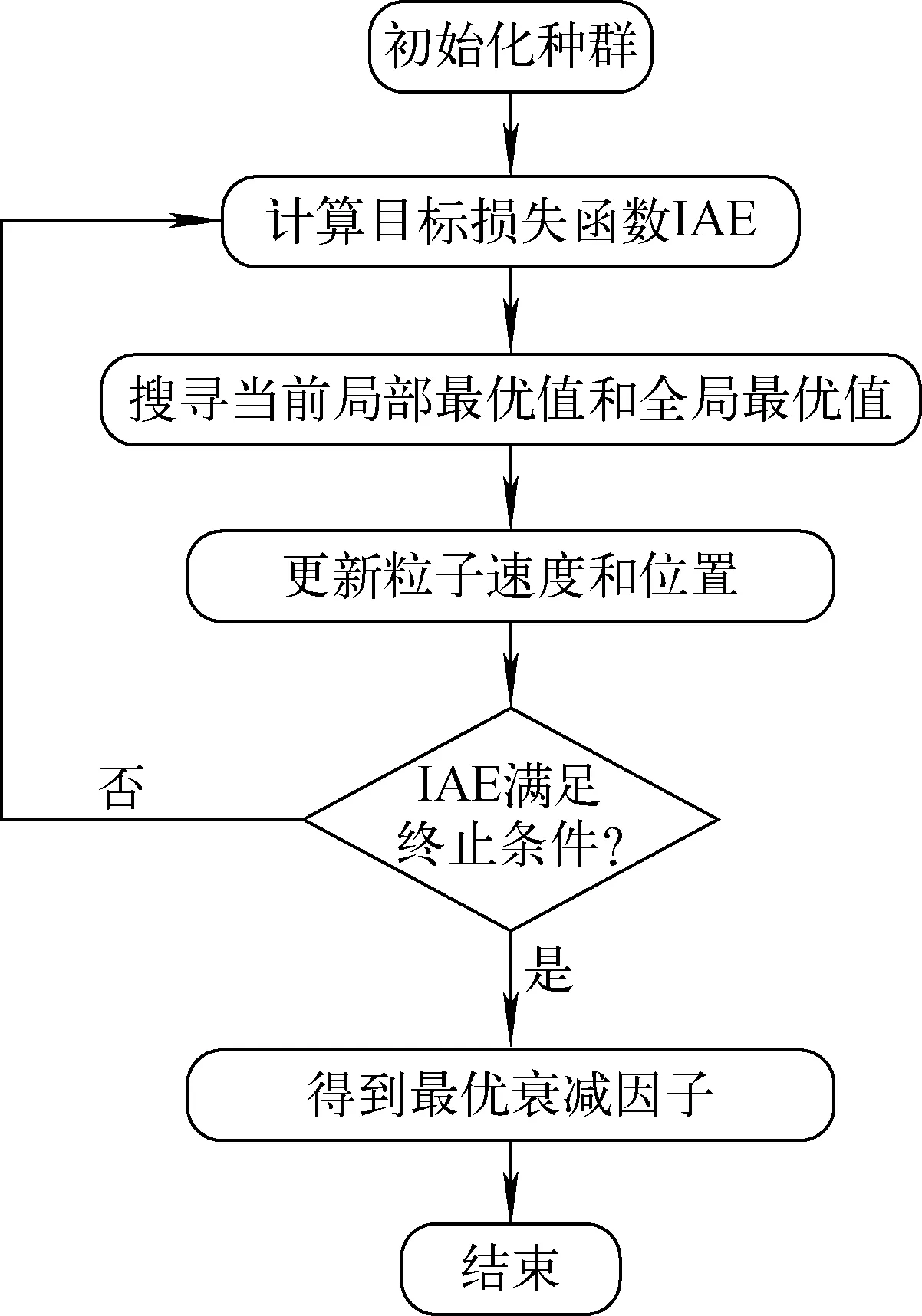
图2 粒子群优化算法流程图Fig.2 Flow chart of particle swarm optimization algorithm
PSO粒子群算法基本思路如下。
(1) 在可行解的空间范围内将一群粒子进行初始化处理,其中每个粒子均代表1个可能的最优解,用位置、速度及适应度这3个指标描述单个粒子的特征。各粒子的适应度是通过定义的适应度函数计算所得,其值大小直接决定粒子的优劣,在此,适应度函数定义为被控对象的传递函数G(s)与内部对象模型M(s)的绝对误差积分即IAE。
(2) 当粒子在三维空间中运动时,通过个体极值和群体极值的大小求得新的一群粒子。
(3) 每当产生新粒子群时,再次计算该群粒子的适应度。通过将新的粒子的适应度与原来的上一代粒子群的个体最优和群体最优值进行比较,从而得到更适合的个体最优值和群体最优值。最后进行不断迭代更新,直到符合输出条件。
3) 基于模型失配的内模控制器设计
由于在工程上很难使辨识所得对象与过程模型完全相等,故只需模型足够精确,使得:
M(s)≈G(s)
(43)
即可满足条件[9-15]。
当θ较小时,对于m=1,时滞项e-θ s用1阶Pade公式进行近似,如下式所示:
(44)
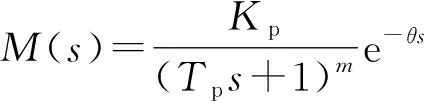
当m≥2时,时滞项e-θ s用2阶泰勒公式近似为下式:
e-θ s≈1-θs+0.5θ2s2
(45)
若m>2或m=2,e-θ s≈1-θs+0.5θ2s2,则将包含所有左半平面零点的传递函数作为M-(s),包含所有右半平面零点的传递函数作为M+(s)。
根据图1,可得到控制器总体系统过程数学模型,表示为如下形式:
(46)
再将式(36)和(37)代入式(35)中可得到控制器传递函数Q(s)为:
(47)
最后将式(37)和式(47)代入式(46)中可得到控制器模型为:
(48)
本文在辨识过程中选取2阶模型即m=2,从而算得内模控制器具体模型表达式为:
(49)
2.2 堆芯功率内模控制器仿真分析
虑液态熔盐堆一回路系统中燃料熔盐的流动特性,基于MATLAB/Simulink建立熔盐实验堆一回路仿真系统,如图3所示。

图3 基于内模控制的MSRE一回路系统仿真图 Fig.3 Simulation diagram of MSRE loop system based on internal model control
在100%FP堆芯功率水平下,无内模控制器时引入50 pcm的阶跃反应性响应如图4a、b所示。图4a中,当引入阶跃反应性时,无控制器下,系统相对功率偏差超调量大,由于系统内自身的温度负反馈效应,相对功率偏差输出在经历瞬时上升后缓慢下降并稳定在新的输出值上。图4b中,无控制器作用时,系统的热交换器二次侧出口温度、堆芯出口处燃料温度以及堆芯进口处燃料温度与其稳态初始值的偏差在短时间内达到了一个较大的超调量,待达到峰值后逐渐下降,缓慢地达到新的稳定输出值。
在100%FP堆芯稳态功率水平下,有内模控制器时引入50 pcm的阶跃反应性,系统的相对功率偏差响应和温度偏差响应如图4c、d所示。由图4c可知,在内模控制器作用下,系统相对功率偏差在瞬时上升后,又瞬时下降至一个较小的负值,然后快速达到0,系统达到稳定,且相对功率偏差上冲幅度和超调量都显著减小,过渡时间短。系统的温度响应曲线如图所示,在引入反应性后,各温度偏差的超调量显著减小,最后偏差值稳定到0。由此可见,内模控制器能快速、有效地控制液态熔盐堆堆芯功率,控制效果良好。

a、b——无内模控制器;c、d——有内模控制器图4 100% FP功率水平下引入50 pcm反应性时MSRE系统响应图Fig.4 MSRE system response diagram with 50 pcm reactivity at 100% FP power level
3 结语
考虑液态熔盐堆一回路系统中燃料熔盐的流动性对堆芯功率控制的影响,采用集总参数法建立熔盐实验堆一回路系统非线性模型。基于该非线性模型,建立熔盐实验堆一回路线性化模型,结合内模控制理论和粒子群优化算法,设计了熔盐实验堆堆芯功率内模控制器。针对熔盐实验堆运行中出现的反应性阶跃扰动,开展仿真计算。结果表明,所设计的内模控制器能准确、快速地控制堆芯功率,使系统迅速达到稳定。

