基于多次碰撞源的屏蔽计算方法研究

王新宇，张 斌，陈义学

(华北电力大学 核科学与工程学院，北京 102206)

离散纵标(SN)方法是屏蔽计算中常用的算法之一[1]。在离散纵标屏蔽计算中，因对粒子输运方程中空间变量和角度变量的近似处理，不可避免地存在离散误差，特别是屏蔽计算中角通量密度在空间或角度上的分布不光滑甚至间断的情况。射线效应是角度离散化造成的标通量密度呈现空间震荡分布的现象，在带有孔道、孤立点源的屏蔽问题中尤为明显[2-3]。首次碰撞源方法[4-7]通过解析方法或高阶方法求解点源产生的未碰撞角通量密度，计算出每个空间网格在离散方向上的首次碰撞源作为SN计算中的分布源。这样即使在弱散射情况下，粒子也能运动到整个求解空间从而减小角度离散误差。首次碰撞源方法虽能在一定程度上缓解射线效应，但无法解决空间离散导致的数值扩散问题，同时首次碰撞源方法难以处理二次射线效应[8]。对空间变量的离散易导致未碰撞通量密度的数值解出现数值扩散效应，具体表现为数值模拟中粒子的传递偏离真实的方向或粒子在传递过程中不能正确地衰减[9]。离散纵标屏蔽计算中的空间变量离散格式主要可分为有限差分格式[10]、短特征线格式[11]和间断有限元格式[12]等，其中一些空间离散格式虽具备良好的鲁棒性，但不能缓解因角度离散导致的射线效应。

本文基于射线追踪研究一种半解析的多次碰撞源方法，以缓解射线效应和数值扩散对屏蔽计算精度的影响。通过计算在选定区域内粒子发生多次碰撞的通量密度，将粒子每次碰撞看作一个散射的过程。由每次碰撞通量密度(包括未碰撞通量密度)和散射截面计算出选定区域网格的多次碰撞源，将此分布源作为固定源对整个模型进行离散纵标输运计算。然后将每次碰撞通量密度(包括未碰撞通量密度)和输运求解的碰撞通量密度求和，得到整个计算模型的通量密度分布。

1 理论方法

1.1 多次碰撞源方法

稳态单群固定源无裂变输运方程如下：

(1)

Lψ=Sψ+Q

(2)

L为输运算子：

(3)

S为散射矩阵：

(4)

将整个模型分为区域A和区域B两部分，假设选定计算粒子在区域A中碰撞多次的通量密度，区域A需包含源区。由此可得：

L(ψA+ψB)=(SA+SB)(ψA+ψB)+Q

(5)

其中：ψA和ψB分别为区域A和区域B中的通量密度，两者之和表示整个模型内的角通量密度分布情况；SA和SB分别为区域A和区域B中的散射矩阵，两者之和表示整个模型内的散射矩阵的分布。在区域A内的ψB根据其物理意义均等于0，此时源区对区域A的通量密度占主要贡献，将式(5)进行化简后可得到：

LψA=SψA+Q

(6)

式(6)描述粒子在区域A运动的过程，区域B的通量密度来自区域A的通量密度的贡献，即在后续计算中将区域A看作模型的源区，式(5)、(6)联立后可得式(7)：

LψB=SBψA+(SA+SB)ψB=SBψA+SψB

(7)

由式(6)可得：

(8)

(9)

LψSN=SψSN+Q(n+1)

(10)

最终，由两步输运结果之和得到总通量密度，即：

(11)

多次碰撞源方法的主要思想在于将粒子每次发生碰撞的过程独立处理，与标准的SN方法的源迭代求解流程有所区别。在计算粒子每次发生碰撞的过程时采用半解析的射线追踪方法[13]，尽量减少因角度离散和空间离散引起的离散误差，更准确地描述粒子在模型内的输运行为。多次碰撞源方法具有一些积分输运方法的性质。当选定的计算区域和碰撞次数均取极限值，即是计算整个模型内粒子碰撞无穷次后的通量密度分布情况，与标准的SN方法的源迭代求解流程所描述的物理过程一致。

1.2 求解流程

标准的SN方法求解方法是对群内散射源进行迭代计算，迭代方程如下：

(12)

(13)

其中：D为离散角度转化为矩的算符；φ(l)为通量矩；ε为迭代的收敛准则。令迭代初始值φ(0)=0，ψ(n)即为至多经历n次碰撞的粒子角通量密度。在源迭代过程中得到的ψ(0)，ψ(1)，…，ψ(n)分别为粒子未经碰撞的角通量密度，经1次碰撞的角通量密度，…，经n次碰撞的角通量密度。

选取Kobayashi基准题模型Ⅱ[14]分析迭代过程中模型内的通量密度分布情况。Kobayashi基准题模型Ⅱ的几何结构如图1所示。源强S和截面信息列于表1。

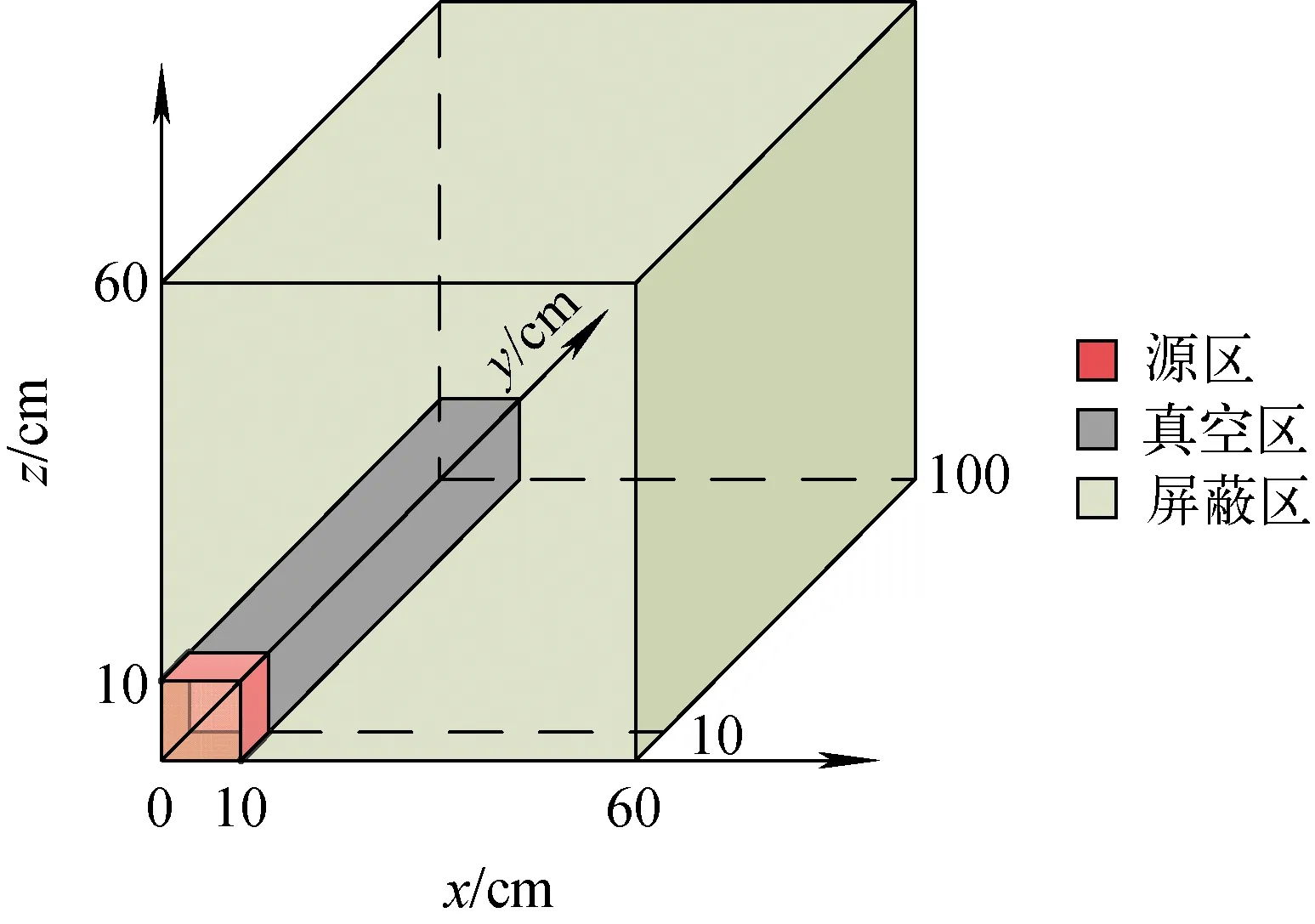
图1 Kobayashi基准题模型Ⅱ几何示意图Fig.1 Geometry of Kobayashi benchmark problem model Ⅱ

表1 源强与截面信息
Table 1 Source strength and cross section

区域S/(cm-3·s-1)Σt/cm-1Σs/cm-1源区10.10.05真空区010-40.5×10-4屏蔽区00.10.05

为尽可能减少离散误差的影响，将模型划分为步长为1 cm的60×100×60的空间网格集合，空间离散格式选择置零修正的菱形差分格式，采用100阶勒让德-切比雪夫求积组进行计算，图2为当源迭代过程进行到第n次时，模型内ψ(n)的分布情况。

从分布形状上看，在初始几次迭代中标通量密度在空间上分布呈现非物理振荡，而随后的散射过程会使整个模型空间内的标通量密度的分布趋于光滑，标通量密度的分布是随着迭代的进行越来越广且各向同性越来越强的，其非均匀性逐渐减弱。数值结果表明，对于带有孔道的屏蔽问题，前几次迭代的标通量密度数值上相对较大且主要分布在孔道内，随着迭代的进行标通量密度逐渐减小。因此仅在计算未碰撞通量密度和前n次碰撞通量密度时采用半解析的射线追踪方法，后续的碰撞通量密度采用SN方法求解：

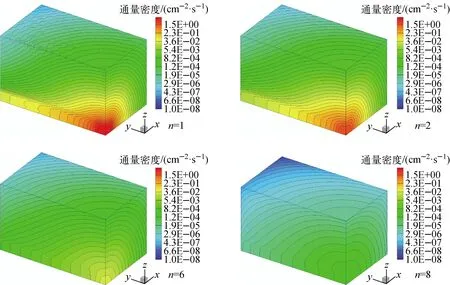
图2 Kobayashi基准题模型Ⅱ内通量密度分布示意图Fig.2 Flux density distribution in Kobayashi benchmark problem model Ⅱ

(14)

其中：ψ(i)为粒子第i次碰撞的通量密度；Q(i)为粒子第i次碰撞时的源项。射线追踪方法主要在于计算粒子在几何空间中从ro点穿行到rp点的径迹长度，即光学距离τ(ro,rp)，其表达式如下：

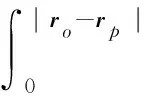
(15)

其中：μ为粒子运动方向的角余弦；Σt(ro+μΩrp)为ro+μΩo→p位置点的总截面，Ωo→p是从ro点穿行到rp点的单位向量。根据角通量密度的球谐矩定义：

(16)

碰撞角通量密度的球谐矩可由式(14)和式(16)确定：

(17)

采用多次碰撞源方法计算粒子在整个模型空间内碰撞无穷次的情况时，总通量密度ψtotal的迭代求解流程如式(18)所示，表现出多次碰撞源方法的积分性质。

Lψ(1)=Q,Sψ(2)=Sψ(1),…,Lψ(n)=Sψ(n-1)

(18)

2 基准验证

2.1 自设屏蔽问题

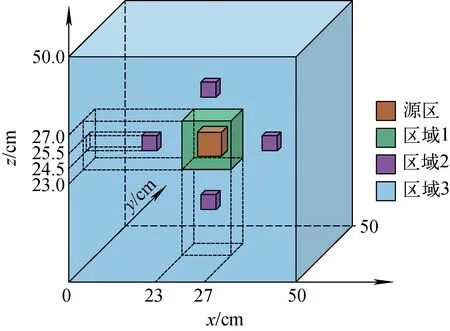
图3 自设屏蔽问题几何模型Fig.3 Geometric model of self-designed shielding problem

该自设屏蔽问题几何模型如图3所示，尺寸为50 cm×50 cm×50 cm，边界条件均为真空边界；源区位于模型中心边长为2 cm的立方体，中子源强为1 cm-3·s-1；源区外围是一层尺寸为4 cm×4 cm×4 cm的高散射比材料；屏蔽层内分布着4个总截面较大的立方体块，尺寸为1 cm×1 cm×1 cm。具体的截面信息列于表2。

表2 自设屏蔽问题的截面信息Table 2 Cross section of self-designed shielding problem

该问题源区的四周分布有总截面相对较大的高散射比单元，因射线效应形成的粒子束穿过这些单元时可能会导致新的或次要的射线效应，采用首次碰撞源方法修正不能消除由这些单元产生的二次射线效应，需更高次的碰撞源修正方法。

整个模型被划分为步长1 cm的50×50×50空间网格集合，采用16阶勒让德-切比雪夫求积组，置零修正的菱形差分格式。分别使用标准SN方法、首次碰撞源方法和多次碰撞源方法计算通量密度分布，其中多次碰撞源方法的计算区域为源区和区域1，碰撞次数为2次。3种方法的计算时间分别为26、25和26 s，计算结果如图4～6所示，首次碰撞源方法在一定程度上缓解了离散误差，但射线效应依然十分明显，而多次碰撞源方法减弱二次射线效应的效果更加显著。

2.2 Kobayashi基准题模型Ⅲ

Kobayashi基准题是经济合作和发展组织核能机构(OECD/NEA)辐射输运专家组提出的用于验证输运程序屏蔽计算能力的基准题。选取Kobayashi基准题模型Ⅲ，用标准SN方法、首次碰撞源方法和多次碰撞源方法分别进行计算，分析多次碰撞源方法的计算精度、计算效率及离散误差的消除效果。

a——整体模型；b——y=25 cm平面图4 SN方法计算的通量密度分布Fig.4 Flux density distribution calculated by SN method

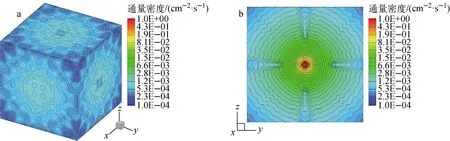
a——整体模型；b——y=25 cm平面图5 首次碰撞源方法计算的通量密度分布Fig.5 Flux density distribution calculated by first collision source method

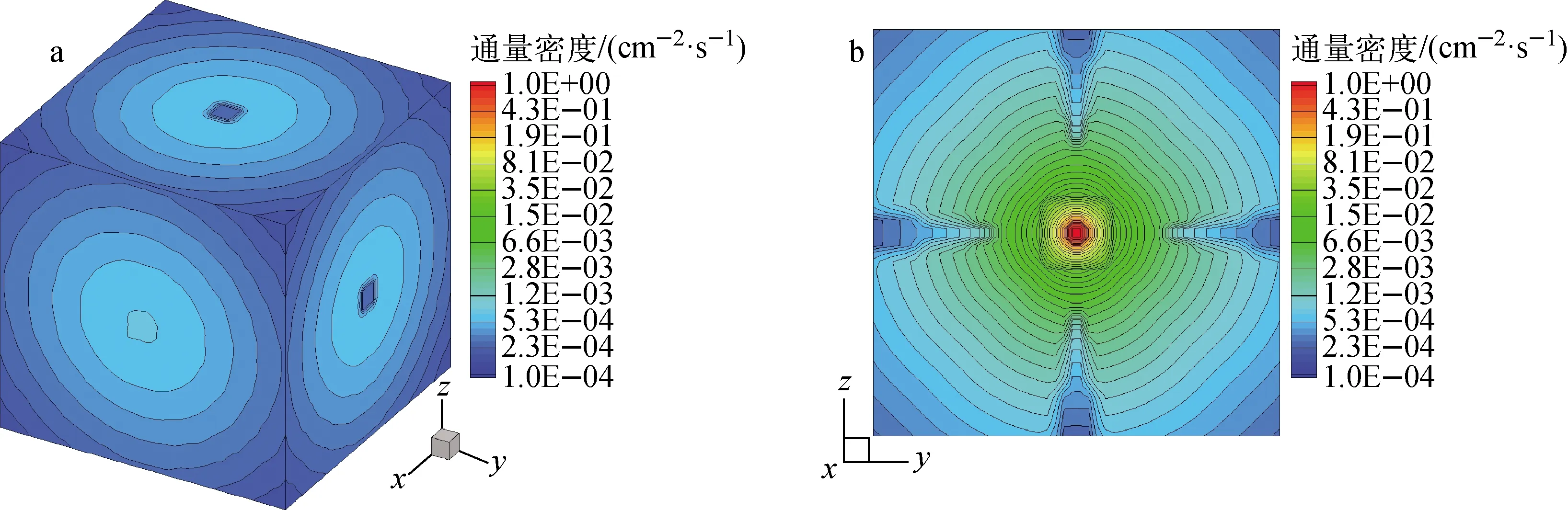
a——整体模型；b——y=25 cm平面图6 多次碰撞源方法计算的通量密度分布Fig.6 Flux density distribution calculated by n’th collision source method

该模型是一个具有折线形孔道的深穿透屏蔽问题，几何模型如图7所示。孔道内的角通量密度分布呈现强各向异性，且孔道与屏蔽区交界面处的通量密度梯度极大，存在较大的离散误差。源强与截面信息列于表1，选取基准报告中提供的沿孔道的22个坐标点作为关键点输出。

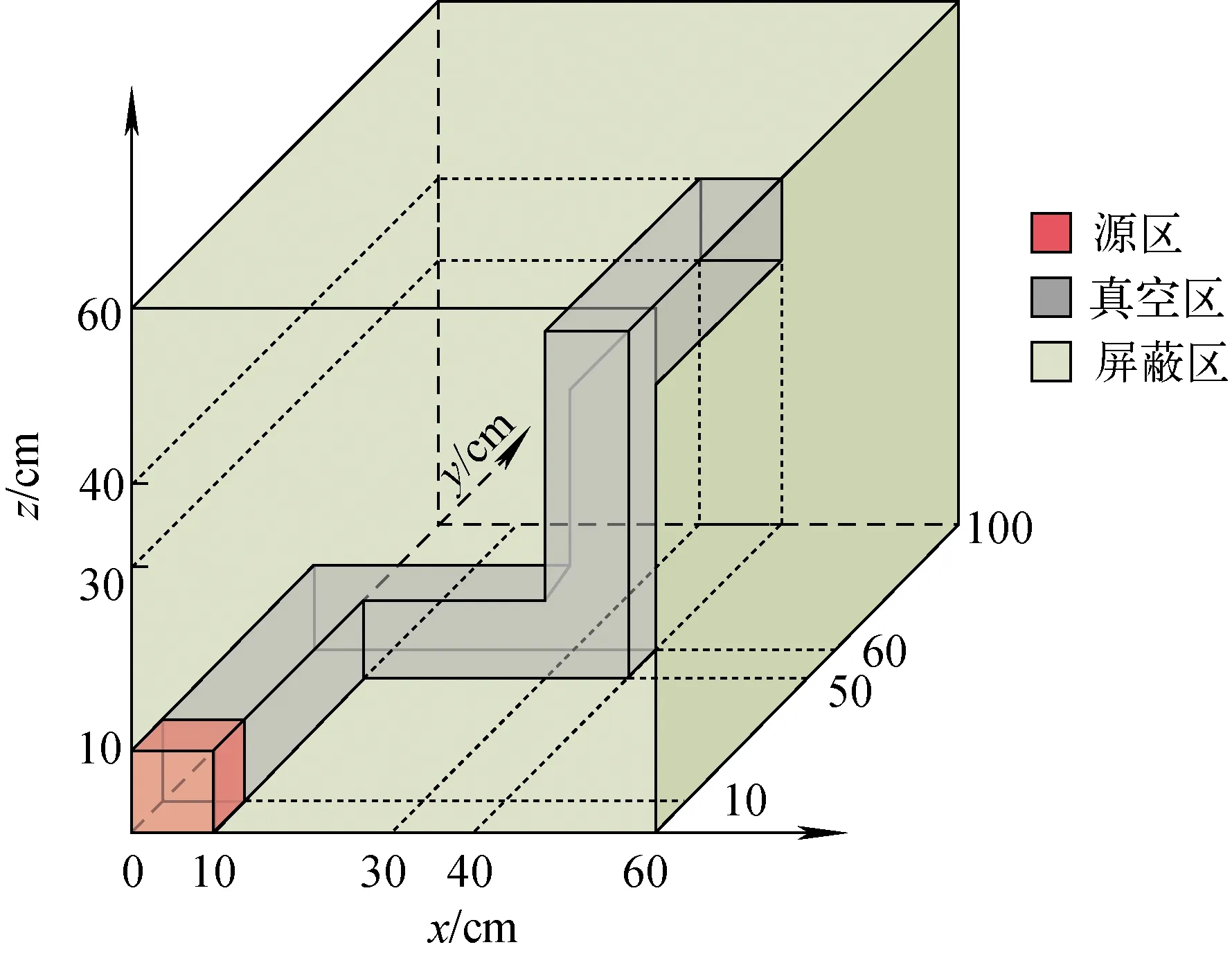
图7 Kobayashi基准题模型Ⅲ几何示意图Fig.7 Geometry of Kobayashi benchmark problem model Ⅲ

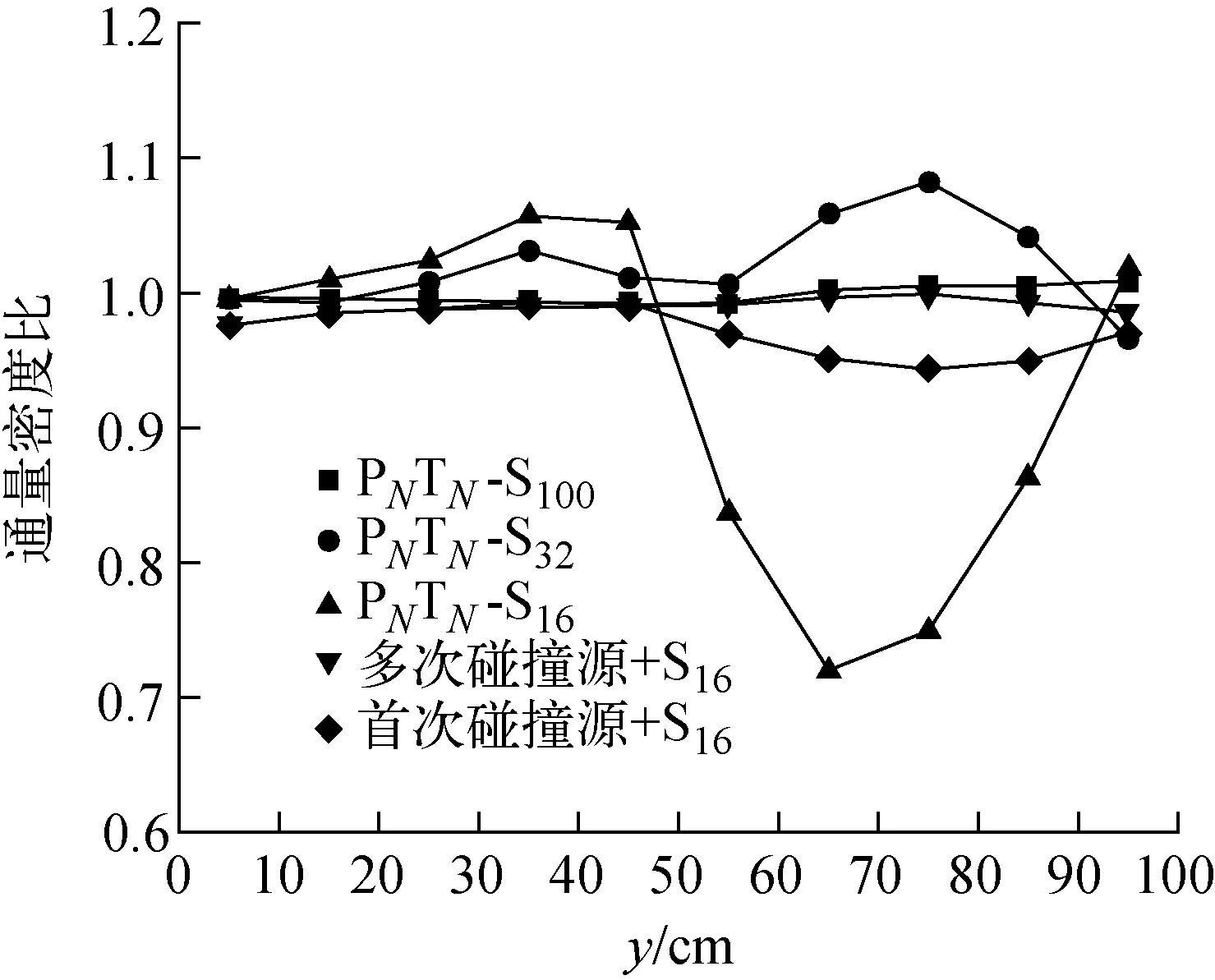
图8 Kobayashi基准题模型Ⅲ关键点通量密度计算值与基准值之比Fig.8 Ratio of calculated value and benchmark value in Kobayashi benchmark problem model Ⅲ

模型划分为步长2 cm的30×50×30空间网格集合，选取置零修正的菱形差分格式，迭代收敛准则为1×10-4。以基准报告中提供的蒙特卡罗程序计算结果作为参考值，分别采用SN方法、首次碰撞源方法和多次碰撞源方法的计算值与参考值进行比较，其中多次碰撞源方法的计算区域为源区和屏蔽区，碰撞次数为2次，沿y轴关键点的相对误差变化曲线如图8所示。数值结果表明，孔道的存在导致角通量密度的各向异性程度随距离增加而增强。当采用16阶勒让德-切比雪夫求积组计算时，孔道内的中子通量密度非物理震荡强烈；当求积组的阶数提高，采用100阶PNTN求积组进行计算，通量密度的相对误差随距离的增加仍呈现逐渐上升的趋势。采用首次碰撞源方法计算时，同样使用16阶PNTN求积组计算得到的相对误差整体小于10%，但离散误差的影响并未完全消除。另一方面，由于射线追踪的性质，首次碰撞源方法低估了源区附近的未碰撞通量密度。采用多次碰撞源方法计算时，使用16阶PNTN求积组计算结果的相对误差整体小于5%，相对误差的均方根和标准差均有所降低，多次碰撞源方法也存在低估源区附近通量密度的问题。

表3列出了16阶PNTN求积组、首次碰撞源方法和多次碰撞源方法的计算值与参考值的相对误差和计算时间。数值结果表明，多次碰撞源方法的相对误差均方根小于3%，相对误差的标准差为1.025 2×10-2，消除离散误差的能力优于另外两种计算方法，但计算效率方面，相同情况下多次碰撞源方法的计算耗时较长，原因主要是多次碰撞源方法计算多次碰撞通量密度时，需对所选区域的每个网格进行射线追踪，因此多次碰撞源方法的计算量与所选计算区域的网格数密切相关。

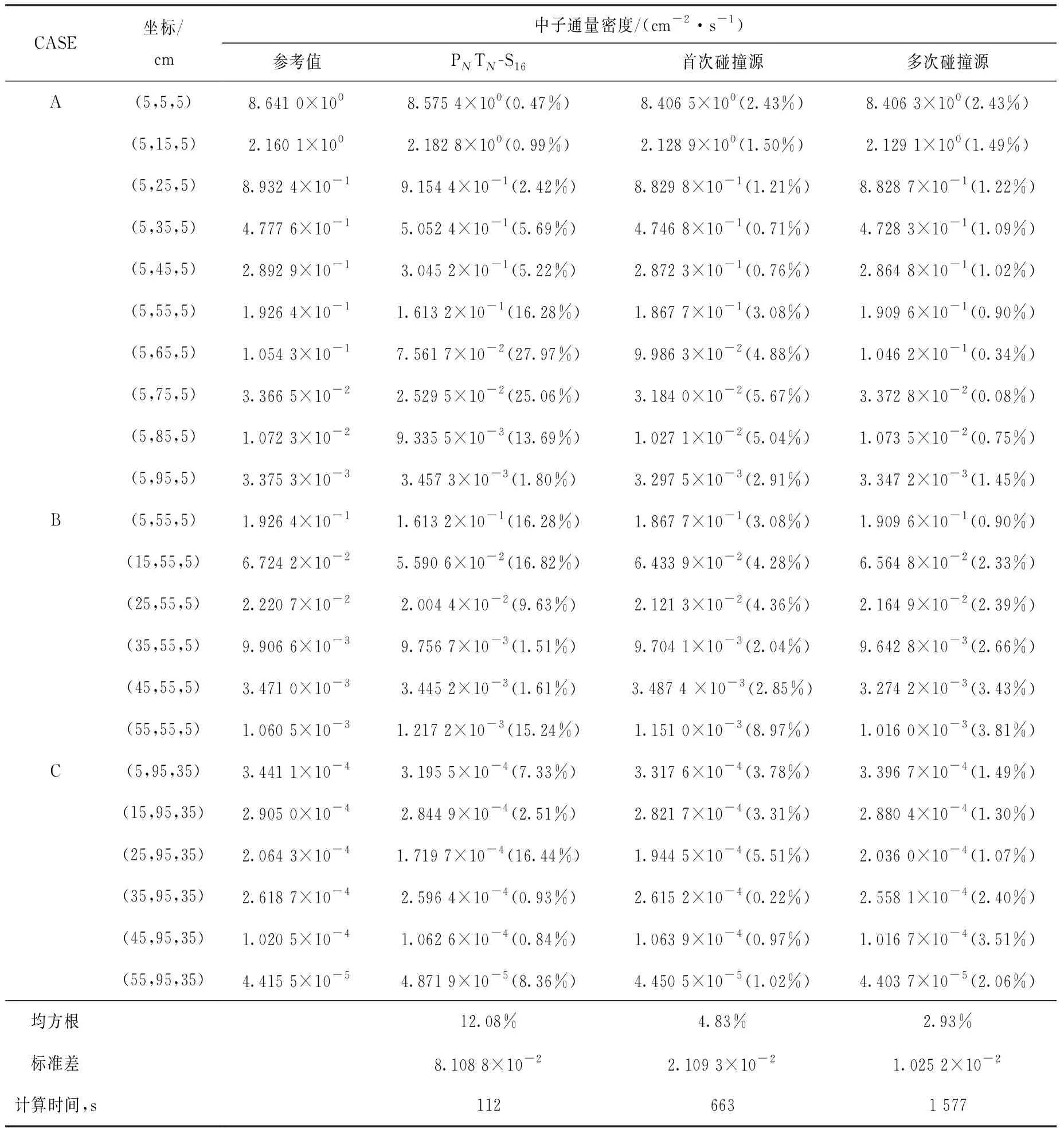
表3 Kobayashi基准题模型Ⅲ计数点位中子通量密度Table 3 Neutron flux density at key point for Kobayashi benchmark problem model Ⅲ

注：括号内为相对误差

2.3 自设多群固定源问题

为了分析多次碰撞源方法对多群屏蔽问题的计算精度，自设均匀介质固定源问题。该自设问题几何模型如图9所示，尺寸为10 cm×10 cm×10 cm，边界条件均为真空边界，材料为304不锈钢[15]；源区位于模型中心为边长1 cm的立方体，中子源强为1 cm-3·s-1，能量为14 MeV。计算采用30群的MATXS-10截面库，各向异性散射P3阶展开，网格尺寸为0.25 cm，100阶PNTN求积组的计算结果作为参考解。

图9 固定源问题几何模型Fig.9 Geometric model of fixed-source problem

图10 探测器中子能谱Fig.10 Neutron spectrum of detector

图10为标准SN方法、首次碰撞源方法和多次碰撞源方法在探测器处的能谱结果，其中多次碰撞源方法的计算区域为整个模型区域，碰撞次数为2次，且仅在第2群(13.5～15 MeV)使用多次碰撞源方法。在能量较低的能量区间内各种方法的计算结果与参考解相近，但在0.1 eV～14 MeV能量区间内仅有多次碰撞源方法与参考解吻合较好。这是由于高能部分的群内散射截面较小同时各向异性散射较强，导致能量最高能群的角通量密度分布各向异性程度最强，第2群的角度离散误差最大，射线效应最严重。而随着粒子的慢化，较低能量能群的角通量密度各向异性程度减弱。通过比对计算，验证了多次碰撞源方法可有效减弱离散误差，具有较高的可靠性。

表4列出不同条件下的计算时间，多次碰撞源方法的计算时间与16阶PNTN求积组和首次碰撞源方法的计算时间相比耗时较长。综合计算精度考虑，多次碰撞源方法相较于100阶PNTN求积组，两者精度相近，计算时间的加速比为3.49。

表4 不同条件下的计算时间Table 4 Calculation time of different conditions

3 结论

针对屏蔽计算中强非均匀效应造成离散误差过大的问题，研究了基于射线追踪技术的多次碰撞源方法。多次碰撞源方法通过射线追踪计算指定区域网格内粒子碰撞多次的通量密度，将孤立源等效为模型内的分布源，在求积组阶数较低时仍可得到准确的结果，有效地消除了离散误差对屏蔽计算精度的影响。数值计算结果表明，多次碰撞源方法相比首次碰撞源方法具有消除次级射线效应的能力，且能缓解因离散误差导致的射线效应和数值扩散现象。