清漂无人船船体轻量化研究

张楚鹏， 陈 铭， 张道德

(湖北工业大学机械工程学院， 湖北 武汉 430068)

无人船能更有效地利用船体空间，增加垃圾打捞量，通过自主巡航打捞垃圾，节省能源，更加绿色环保[1]。对无人船而言，其续航能力是关键，在电池容量一定的情况下，如要提高无人船续航，需尽量降低全船质量，而船体质量占比最大，因此对无人船船体展开轻量化研究可提升续航和降低成本。

船舶结构的优化设计方法主要可分为基于规范的经典优化方法、直接计算法以及基于代理模型的优化方法三种[2]。曾广武[3]等人利用经典优化法对舰船纵向尺寸进行了优化；Li Sun[4]等人运用直接计算法对某集装箱船中部结构进行优化；史亚朋[5]等人利用基于代理模型的优化方法对某大型油船中部结构进行优化。其中，基于代理模型的优化方法用近似数学模型来代替耗时的有限元分析，成为船舶结构优化新的趋势[6-8]。

单隐含层BP神经网络处理简单问题，且需要连续函数来逼近，而清漂无人船结构参数较多，受力复杂，用单隐含层神经网络拟合效果并不理想。鉴于此，本文研究改进单层BP神经网络隐含层神经元节点数，增加隐含层数，提高神经网络的计算精度，并比较不同隐含层神经网络的性能，确定基于双隐含层BP神经网络的结构优化模型，并运用到清漂无人船轻量化中，对优化后的结果进行有限元验证分析。

1 船体优化方案

在进行基于代理模型的结构优化设计时，结构优化数学模型三要素必须确定，即：设计变量、约束条件以及目标函数[9]。

1.1 船体设计变量的选择

以自主研制的清漂无人船为研究对象。该船长5 m，宽2.4 m，为单甲板、单底板、单舷侧的双船体结构。全船为钢制船，采用横骨架式结构，有清漂装置的固定筋，两船身的连接桥，单船设有1根中内龙骨，10根横向肋板。清漂无人船的体积相对较小，参数变量较少，故忽略局部细节，将所有构件作为设计变量进行分析。采取参数试验法对船整体构件进行灵敏度分析[10]，依此来确定优化过程中涉及的设计变量。清漂无人船如图1所示。

图 1 清漂无人船体

1.2 约束条件

根据中国船级社《钢制内河船舶入级与建造规范(2016)》[11]，确定其中主要构件厚度尺寸约束条件为：肋板不小于35.4 mm；甲板横梁不小于35.7 mm；甲板纵桁不小于47.1 mm；船底板舱壁不小于2.4 mm。船舶所受到的等效应力、剪应力最大值约束限制如下：

(1)

σmax和τmax通过BP神经网络拟合的应力与板厚函数确定，[σ]=220 MPa,[τ]=115 MPa。

1.3 船体优化目标函数

基于物理学质量公式，以清漂无人船船体质量最轻为优化目标建立目标函数，其数学表达式为：

(2)

式中：M为船上固定设备重量；n为构件数量；Vk为第k个构件的体积；ρk为第k个构件的密度；Sk为第k个构件的面积；Tk为第k个构件的厚度。

2 基于参数试验法的船体灵敏度分析

2.1 原厚度尺寸船体有限元分析

清漂无人船船上搭载有清漂装置、垃圾收纳盒、垂直风机、蓄电池、电气控制柜、抽水泵，总质量为997.6 kg，满载时船吃水线深为500 mm。部件分布如图2所示，各部件质量如表1所示。

1-太阳能板；2-垂直风机；3-清漂装置；4-抽水泵； 5-蓄电池；6-电控柜；7-垃圾收纳盒图 2 船体固定部件分布

表1 各部件质量

设备名称m/kg数量/个(台)蓄电池142.52电机502垃圾收纳盒501电气控制柜601抽水泵42.61清漂装置801太阳能板27.29垂直风机28.754

按照最危险工况(即满载情况)对船体、固定筋以及船身连接桥进行有限元分析，并计算由水面以及船身所引起的固有频率，船体采用普通低碳钢建造，其密度为7.85×103 kg/m3；杨氏模量为2.1×105 MPa；重力加速度为9.8 m/s2；泊松比为0.3；屈服强度为235 N/mm2。

通过分析得出全船最大等效应力为116.13 MPa,最大剪应力为60.737 MPa，小于规范要求，有优化的空间。应力分析结果以及1阶、2阶固有频率如图3、4所示。

图 3 应力云图

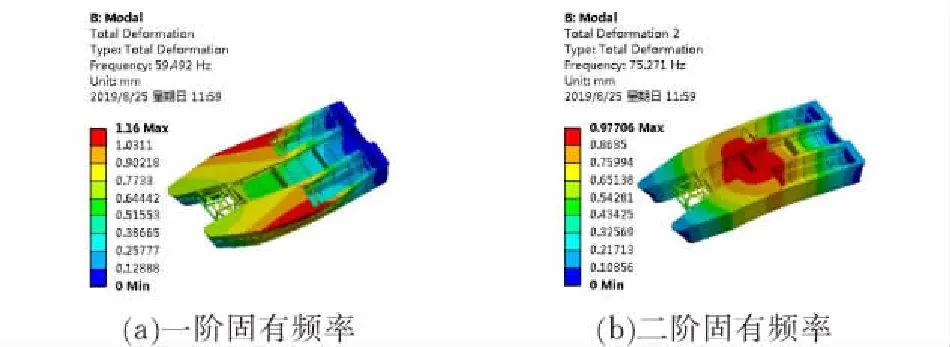
图 4 船体固有频率

2.2 船体构件灵敏度分析

用SolidWorks建立改变清漂无人船各构件厚度参数的模型，运用ANSYS有限元分析软件来计算改变构件参数后，船体的等效应力最大值、剪应力最大值、质量以及1阶、2阶固有频率的响应变化。对试验数据进行整理，部分结果如图5所示。

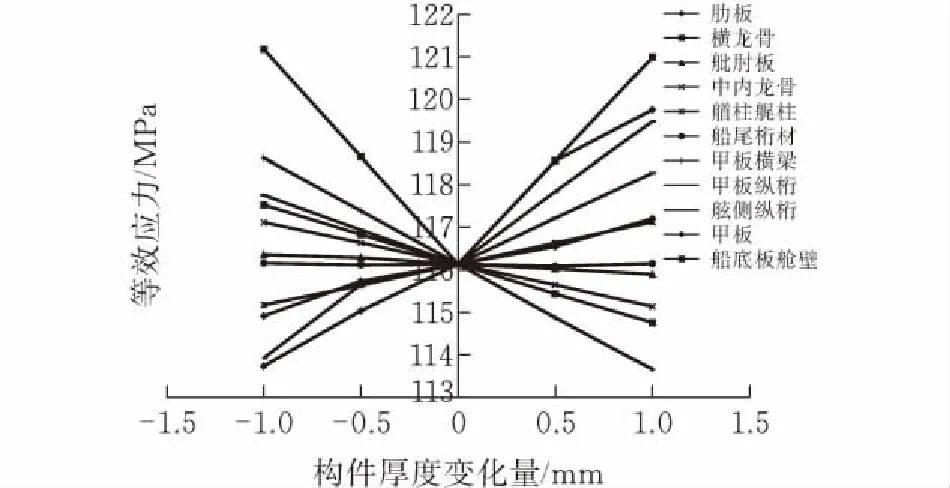
(a)等效应力

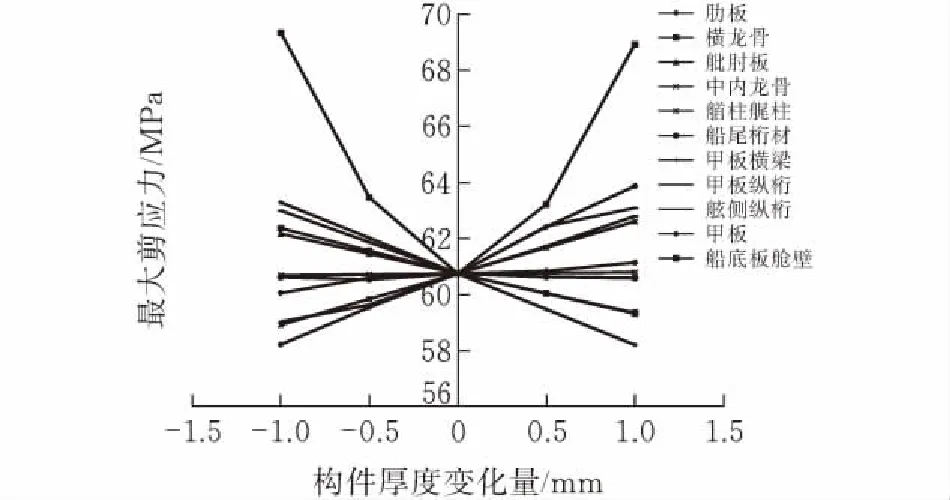
(b)剪应力

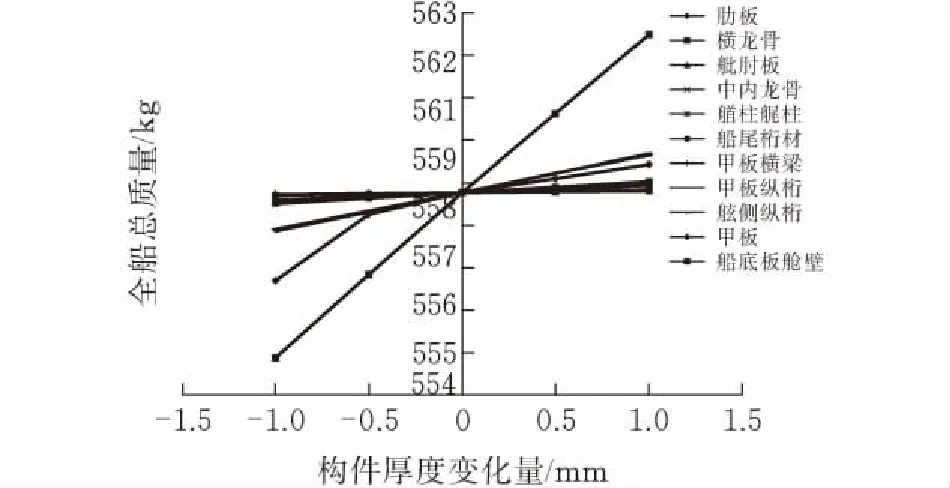
(c)全船质量

(d)一阶固有频率图 5 灵敏度分析结果

对图5结果进行分析，将改变构件几何参数后对应力、质量以及固有频率影响小的构件因素筛选剔除，发现：肋板、甲板横梁、甲板纵桁以及船底板舱壁等构件对等效应力、剪应力影响较大；船底板舱壁、肋板对质量影响较大；船底板舱壁、龙骨对固有频率影响较大。综合考虑，将肋板、甲板横梁、甲板纵桁以及船底板舱壁等构件作为有效的设计变量。

3 船体双隐含层BP神经网络的建立

利用MATLAB构建反映设计变量与最大等效应力、最大剪应力映射关系的BP神经网络，并对其进行训练和测试。发现单隐含层BP神经网络的拟合情况并不理想，决定系数略小，相对误差较大。针对此问题，提出构建基于双隐含层的BP神经网络，增加隐含层神经元节点，提高神经网络传递时的计算精确率，以此来减小相对误差，达到更好的拟合效果，并与三、四隐含层BP神经网络进行性能比较。双隐含层BP神经网络结构如图6所示。

图 6 双隐含层BP神经网络

图6中，x为输入设计变量，y为应力输出，P1至Pn为输入层神经元节点，1至S1为第一隐含层神经元节点，1至S2为第二隐含层神经元节点，T为输出层神经元节点。

3.1 BP神经网络结构设计

将灵敏度分析得出的肋板、甲板横梁、甲板纵桁以及船底板舱壁等构件的厚度变量作为神经网络的输入，构造4因素5水平的正交表，进行正交试验[12]，得到100组作为神经网络训练和测试样本的数据，其中80组数据用于训练样本，20组数据作为测试样本，将最大剪应力和等效应力值作为神经网络的输出，构造2个BP神经网络。

神经网络输入层节点数由输入变量数决定，取4个节点；输出层节点数由应力输出决定，取1；隐含层节点数由经验公式确定，其表达式如下：

第一隐含层

l=2m+1

(3)

多隐含层

(4)

式中：l为隐含层节点数；m为输入节点数；n为输出节点数；a为1～10间的调节常数。

据此构建单隐含层、双隐含层以及三、四隐含层BP神经网络结构。

3.2 BP神经网络训练与检测

对构造的BP神经网络在最小均方误差、学习率、最大迭代次数一致的情况下进行训练，具体参数设置如表2所示。

表2 BP神经网络训练

训练完成后，比较这几类BP神经网络应力输出的真实值与预测值的拟合情况，以及决定系数R2，其范围在[0,1],其越接近1，表示模型的性能越好，反之代表模型性能越差。其拟合效果见图7。

图 7 四类BP神经网络输出结果拟合

由图7可见，双隐含层BP神经网络决定系数R2=0.93768，相比于单隐含层BP神经网络决定系数(0.39175)、三隐含层BP神经网络决定系数(0.5414)、四隐含层BP神经网络决定系数(0.78374)，其拟合效果更好，更趋近于1。

计算比较这几类BP神经网络训练误差，其训练误差如图8所示，其误差表达式：

(5)

式中：p为第p个样本；n为样本数；di(p)为第p个样本的预测值；yi(p)为第p个样本的真实值。

图 8 四类BP神经网络训练误差

由图8可算出单隐含层BP神经网络训练误差为0.068，双隐含层BP神经网络训练误差为0.0135，三隐含层BP神经网络训练误差为0.0509，四隐含层BP神经网络训练误差为0.1565，比较得出双隐含层误差更小，精度更高。故本文构建的双隐含层BP神经网络能有效、精确反映设计变量与输出应力之间的关系，可作为代理模型代替有限元模型，参与到清漂船结构优化中。

4 全船结构优化与分析

利用结构优化数学模型，全船结构优化表达式：

(6)

式中：x=(x1,x2,…,xn)为需优化的设计变量；f(x)为目标函数；lk(x)=0,(k=1,2,…,K)为设计变量需满足的等式约束条件，船体尺寸约束；gj(x)≤0,(j=1,2,…,J)为设计变量满足的不等式约束，BP神经网络拟合的应力与板厚函数。

将肋板、甲板横梁、甲板纵桁以及船底板舱壁等构件作为优化的设计变量，利用相关规定中的尺寸约束以及BP神经网络中预测的构件厚度与等效应力、最大剪应力非线性函数作为约束条件，将清漂无人船质量最轻函数作为目标函数，进行全船结构优化。优化以后，全船质量从568.775 kg减少至510.191 kg，质量减少10.3%左右。构件尺寸结果如表3所示。

表3 优化前后构件尺寸结果对比 mm

依照表中数据，对清漂船参数进行修改，对优化后的清漂船进行有限元分析，部分结果如图9所示。

图 9 应力云图

由图9可知，优化后的清漂无人船最大等效应力为155.45 MPa,小于[σ]=220 MPa；最大剪应力为85.231 MPa，小于[τ]=115 MPa，故满足规范设计要求。

将优化后的清漂无人船装载至武汉市蔡甸区高湖进行试验，其满足吃水航行以及强度要求。试验实物如图10所示。

图10 优化后船体下水试验

5 结论

通过建立清漂无人船全船优化模型，以全船质量最轻为目标优化函数，构造双隐含层BP神经网络作为有限元分析替代模型，根据船舶设计规范来约束应力与厚度尺寸，对清漂无人船进行结构优化，优化后全船质量降低10.3%。对优化后的结果采用有限元分析，优化后的清漂无人船满足规范要求，下水试验成功，证明了双隐含层BP神经网络在清漂无人船结构优化上的可行性。