金融市场系统性风险的动态测度与演化分析——基于时效性视角
荣梦杰, 李 刚
(湖北工业大学 理学院, 湖北 武汉 430068)
测度系统性金融风险的方法主要有信号法、压力指数法、模型法三大类。信号法旨在找出有效的信号指标和合理阈值[1],并不能满足当今金融市场风险测度所需的时效性需求。基于模型法测度系统性金融风险的研究理论大体可分为基于期望损失理论、基于条件在险价值理论和基于Black-Sholes 期权定价模型的未定权益分析(CCA)法[2],但这些模型多是针对传统金融业,鲜有从提高系统性金融风险测度的时效性为着手点而对当今金融业进行的研究。已有研究多是运用固定权重法进行加权[3-8],并不能够准确刻画实际的风险状况。因此,寻找具有良好时效性的系统性金融风险测度方法势在必行。设置动态权重可以大大提高时效性,不少学者在系统性金融风险的动态度量方面进行了探究,例如,Dovern 和 van Roye[9]应用动态近似因子模型计算出了20个主要经济体的金融压力指数,邓创和赵珂[10]基于动态CRITIC赋权法测度了中国金融压力总指数并分析了其变动特征……。虽然上述研究通过动态权重设置满足了时效性要求的动态度量,但都未考虑相近时间点间金融压力的状态转换关系以及对风险信息的提取效果,最终导致测度出的各时间点的金融压力都是孤立间断的,实际捕获的压力信息量大小也无从得知。本文通过结合压力指数法和模型法来实现系统性金融风险度量的时效性要求,并对其风险信息提取能力进行验证,发现利用时变参数状态空间模型测度金融市场系统性金融风险具有良好的“时效性”与风险信息提取能力。
1 模型设定
时变参数状态空间模型主要由两部分组成:一个是量测方程,一个是状态方程。其基本形式可以用式(1)-(3)来描述:
量测方程
(1)
状态方程
ψi,t=c+λiψi,t-1+εi,t
(2)
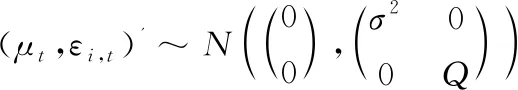
(3)
式中:μt和εt均为随机扰动项,相互独立且服从均值为0、方差为σ2、协方差矩阵为Q的正态分布;Xi,tXi,t代表不同金融子系统金融压力的指标值,Yt是与金融压力的变化相关联的指标,ψi,t为状态变量。
量测方程度量的是因变量随自变量变化而产生的变化,状态方程度量的是整个系统状态随时间变化而产生的变化,即系统的状态变化[11],可以发现运用时变参数状态空间模型(SSM模型)来测度金融压力指数从理论上恰好可以满足时效性要求。
Illing和Liu最早提出金融压力这一概念,指出金融压力是在金融体系内部的不稳定性与外部环境的共同作用下而导致金融体系所承受的压力水平,该压力值能够很好地反映出整个金融系统所面临的系统性风险的大小,并且是与期望金融损失、风险正相关的连续变量,当这个变量达到极值时,就极有可能触发金融危机[12]。当今金融市场风险复杂多变,风险形成、集聚、扩散机制愈加多元化,这对风险度量的准确性、时效性等都提出了更高的要求。参照余辉研究我国金融状况指数的方法[13],本文在研究金融压力指数时各个指标权重的具体计算方法如下:
(4)
式中:WSSMi,t为由SSM模型得到的各子系统在不同时刻的权重,ψi,t为各子系统在不同时刻的参数估计值。
将WSSMi,t带入式(5),计算出相应的金融压力指数
(5)
FSISSMt为通过SSM模型计算得到的t(t=0,1,2,3,…,T)时刻的金融市场压力大小,Xi,t(i=1,2,3,…,n)为不同时刻各金融子系统的金融压力值,各子系统在不同时刻的权重记为WSSMi,t(i=1,2,3,…,n,t=0,1,2,3,…,T)。
2 指标选择
依据代表性原则,各子系统的金融风险压力主要用其相关指标的资产利差和GARCH波动率来衡量。在参照张勇[14]选取指标的基础之上,结合数据频率特征及数据可得性,选取最终的子系统金融压力代理变量如表1所示。此外,本文选取能够代表宏观经济产出变化的工业增加值同比增长率作为关联指标Yt。

表1 金融压力指数指标体系
3 数据来源与预处理
本文选取2007年1月至2018年10月的月度数据分析我国金融市场的系统性金融风险状况,其中,3个月银行间同业拆借利率、3个月国债收益率、1年期和10年期银行间固定利率国债收益率、人民币兑美元汇率数据来源于中国人民银行官网,国房景气指数数据来源于中国金融信息网。相关收益率数据通过式(6)计算,其中,Rt为计算得到的收益率,Pt为t时刻的相应指数值。缺失数据采用均值法进行填补,并将指标进行标准化处理。另外,工业增加值同比增长率序列存在明显的季节效应,故对该序列进行季节调整,其他指标并不存在明显的季节效应,因此不做相应处理。
Rt=lnPt-lnPt-1
(6)
4 实证研究
4.1 单位根与协整检验
为避免伪回归问题,建模前需先对序列进行单位根检验,由于本文数据均为月度数据,因此将检验的最优滞后阶数设置为12,检验结果显示只有forex为平稳序列,其余序列都不平稳,因此需要对不平稳的序列进行差分处理,结果表明差分后的序列为平稳序列。对变量进行基于回归系数的Johansen协整检验,检验结果表明,在0.05的显著性水平下,这6个变量之间存在2个协整关系,变量间确实存在着长期的均衡关系,可以建立时变参数状态空间模型。
4.2 Kalman滤波估计
运用Eviews6.0软件对状态空间模型进行估计。经过反复调参,发现假定状态向量为AR(1)过程的模型估计结果并不理想。因此,借鉴高铁梅[15]处理类似问题的做法,将状态向量定义为递归形式。这种情况下,金融压力指数的状态空间模型定义形式如下:
@signal output=c(1) +α×bank +β×
bond +γ×stock +η×forex +
φ×realty +[var=exp(c(2))]
@stateα=α(-1)、@stateβ=β(-1)、
@stateγ=γ(-1)、@stateη=η(-1)
@stateφ=φ(-1)、@paramc(1)-
0.068427c(2)-0.205018796
其中,c(1)的初始值为output对bank、bond、stock、forex、 realty进行最小二乘回归之后得到的截距项的值,c(2)的初始值计算方法如式(7)所示:
(7)
运用Eviews6.0软件,通过Kalman滤波算法对本文建立的上述时变参数状态空间模型进行参数估计,得到状态空间模型:
outputt=-0.009253+αtbankt+βtbondt+γtstockt+ηtforext+φtrealtyt+[var=exp(-0.4388)]
(8)
状态向量的估计值如图1所示。

图 1 状态向量估计值
为确保模型合理,需进一步对模型残差进行平稳性分析。残差检验结果显示,在0.05的显著性水平下,建立金融压力指数的状态空间模型所得到的残差是平稳的,说明残差中的有效信息提取相对充分,模型合理有效。
4.3 金融市场系统性风险的测度结果
为对比时变参数状态空间模型的实际风险信息提取效果,选取等方差权重法和CRITIC赋权法进行对比分析,结果如图2所示。
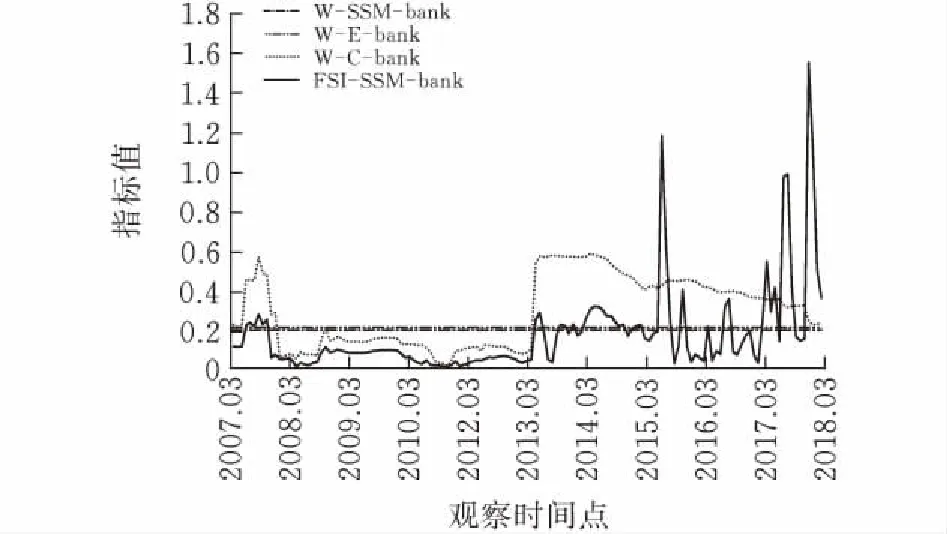
用“W-权重计算方法-子系统压力符号”表示上述三种方法计算出的相应权重; 时变参数状态空间模型法用符号“SSM”表示, 图形上用虚曲线表示; 等方差权重法用符号“E”表示, 图形上用实直线表示; CRITIC赋权法用符号“C”表示, 图形上用虚直线表示;由SSM模型计算出的各子系统风险用符号“FSI-SSM-子系统名称”表示,图形上用实曲线表示。可以看出两种固定权重的差别并不明显,而基于SSM模型计算出的各子系统动态权重围绕固定权重值上下波动,与固定权重交点较少且多数时候都与固定权重有程度不等的偏离,这种偏离实际上是对每个子系统平均风险水平之外的进一步精确刻画,更准确地反映了每一时间点上的风险水平,也充分说明了利用时变参数状态空间模型测度金融市场风险状况具有良好的时效性。

(a) 银行市场风险及三种权重结果对比
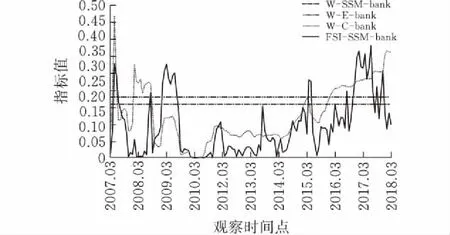
(b)债券市场风险及三种权重结果对比
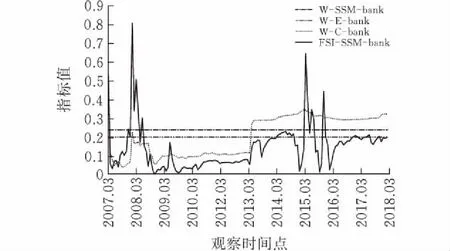
(c)股票市场风险及三种权重结果对比
(d) 外汇市场风险及三种权重结果对

(e)房地产市场风险及三种权重结果对比图 2 各子系统金融风险及三种权重结果对比
观察期内,各个子系统对系统性金融风险的贡献度(即“W-SSM-子系统压力符号”曲线)变化如下:自2013年以来,银行市场和房地产市场的贡献度明显下降,银行市场的贡献占比一直水平较低且波动不大,而房地产市场的贡献占比几乎处于不变的低水平状态,说明近年来银行市场、房地产市场的金融压力相较于其他子系统而言较小且较为稳定。债券市场、股票市场和外汇市场近年来的贡献度明显上升且波动较大,但三者情况又有不同:债券市场在整个观察期内的贡献度呈现近似的倒U型变化,近年来呈现循序渐进上升趋势,而股票市场和外汇市场贡献度则呈现截然不同的进阶式攀升,攀升至较高水平后一直保持不稳定状态,说明我国债券市场、股票市场和外汇市场近年来的金融压力水平较高且非常不稳定。观察期内的金融市场系统性风险演化在2013年前后出现了截然不同的变化趋势,这是由于我国2013年停发IPO整整一年,持续时间最长,另外又由于光大乌龙事件的连续发酵影响,加之央行随后放开了存款利率、扩大了人民币境外市场并于2014年重启IPO等事件的冲击,使得我国的金融市场风险自2013年开始出现幅度较为明显的上升与波动。
计算出基于SSM模型、等方差权重、CRITIC赋权法所得到的金融压力指数,同时反映在图3中。由于运用式(6)使得2007年1月份数据有缺失,为使图形显示效果更佳,在做FSI折线图时人为添加了2007年1月份的FSI数据并设置其值为0,因此2007年1月份到2月份的折线波动不具有实际意义。由图3可以看出,不管是哪种测度方法,都显示近年来我国金融市场的系统性金融风险逐渐上升且波动较大,结合图2中各个子系统的金融风险演化趋势,可以看出近几年的金融市场风险波动主要是由债券市场、股票市场和外汇市场的波动所引起的,银行市场和房地产市场则相对稳定。
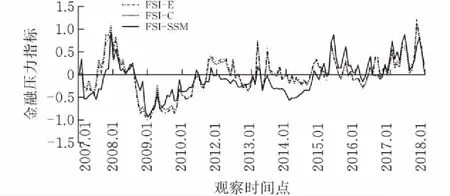
图 3 不同加权方法下的FSI对比
4.4 时变参数状态空间模型的风险信息提取能力
为进一步探究基于SSM模型测度出的金融压力指数是否具有优越的风险信息提取能力,计算出“信息损失量”指标
(9)
其中:InfM表示与基于SSM模型的计算方法相比较而言,通过M方法计算出的金融压力指数的信息损失量;当M取E时,为通过等方差权重法;当M取C时,为通过CRITIC赋权法;WSSM,t为t时刻由SSM模型计算出的权重向量;WM,t为t时刻通过M方法计算出的权重向量;Xt为t时刻代表5个子系统压力的指标值。

表2 固定权重法的风险信息损失量
由表2可以看出,由等方差权重法计算出的金融压力指数序列本身的方差为0.1801,而基于SSM模型计算的金融压力指数在此基础之上多提取了0.0995的风险信息,提高了55.24%的信息提取能力,与CRITIC赋权法相比则提高了60.34%,即与固定权重法相比,几乎都提高了一半以上的风险信息提取能力。
5 结论
本文从时效性的视角,利用金融市场交易数据,分析了中国金融市场系统性风险的动态演化及其现状,得出以下结论:
1)相近时间点间的金融压力转移状态为递归形式,基于此所建立的时变参数状态空间模型在系统性金融风险测度方面具有良好的时效性与风险信息提取能力,更加符合正处于快速成长壮大之中的我国金融市场环境;
2)自2013年以来,我国银行市场、房地产市场对系统性金融风险的贡献度相较于其他子系统而言较小且十分稳定,但债券市场、股票市场和外汇市场对系统性金融风险的贡献度相对较高,但三者呈现完全不同的状况。债券市场自2013年以来对系统性金融风险的贡献度呈现小幅波动上升的趋势,而股票市场的贡献度一直稳定在较高水平,外汇市场则呈现波动幅度较大、水平较高的变化趋势;
3)近几年来我国金融市场的系统性金融风险呈现明显的波动上升,这主要是由债券市场、股票市场和外汇市场的波动所引起的,银行市场和房地产市场则相对较为稳定,这提醒金融监管部门应更加注重对债券市场、股票市场和外汇市场的风险防控。

