2019年全国高考卷Ⅲ第23题的推广及应用
2020-05-30 04:07重庆三峡学院数学与统计学院404000兰晨曦陈晓春
中学数学研究(江西) 2020年4期
重庆三峡学院数学与统计学院 (404000) 黄 浩 兰晨曦 陈晓春
2019年高考全国卷Ⅲ第23题(1):
设x,y,z∈R,且x+y+z=1,求(x-1)2+(y+1)2+(z+1)2的最小值.

上述不等式为条件不等式,将其一般化,可得到如下的不等式:
不等式1 设x,y,z,x0,y0,z0∈R,且Ax+By+Cz=S,其中A,B,C,D是常数,且A2+B2+C2≠0,则(x-x0)2+(y-y0)2+(z-z0)2≥
再将结论的左边添加系数并将指数推广有:
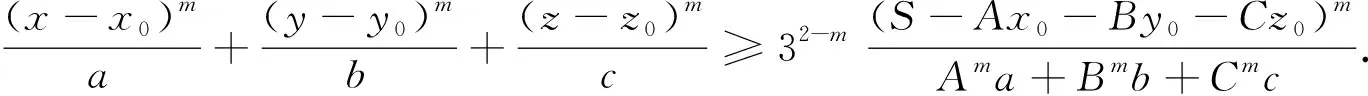

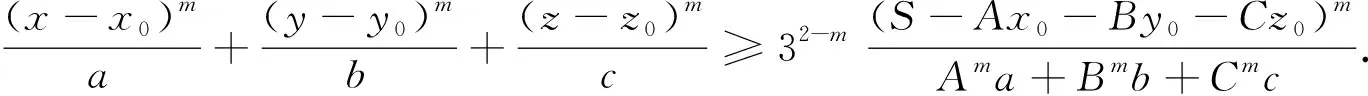
特别地,当A=B=C=1,x0=y0=z0=0时有:

不等式2及不等式3,结构对称,形式优美,对证明分式不等式十分有效,下面举例说明:
例1 已知a,b,c为正数,且满足abc=1,证明:(a+b)3+(b+c)3+(c+a)3≥24.(2019年高考全国卷Ⅰ第23题(2))


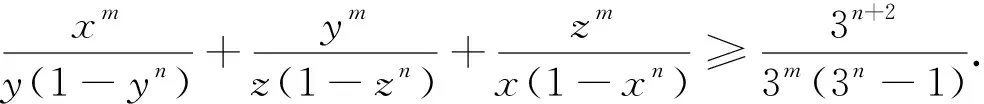
证明:记原不等式左端为M,注意到在条件x+y+z=1,由幂平均不等式有xn+1+yn+1+zn+1≥


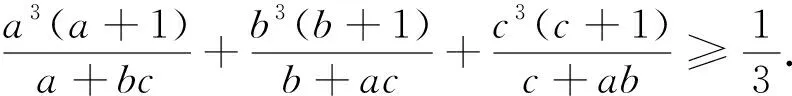

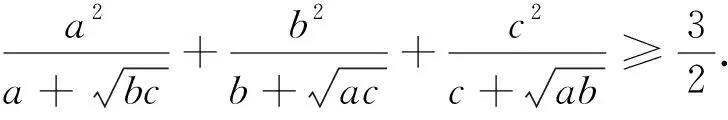

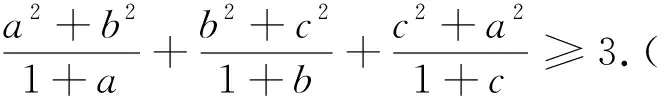
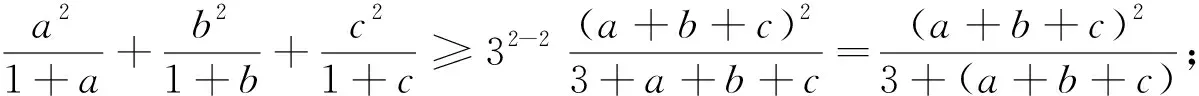
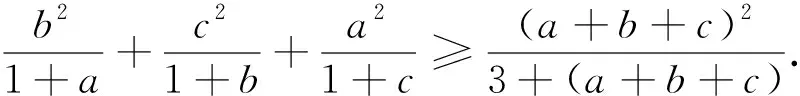
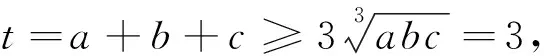

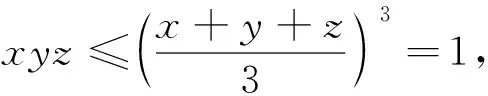
从不等式2的证明可以看出,可将不等式2及不等式3进一步推广为:
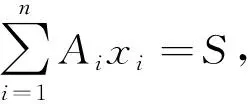

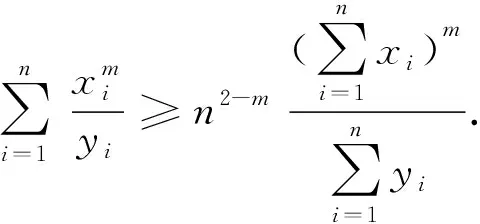
猜你喜欢
语数外学习·高中版中旬(2020年2期)2020-09-10
艺术大观(2019年33期)2019-10-12
美与时代·美术学刊(2017年12期)2018-01-29
美与时代·美术学刊(2017年11期)2018-01-21
中学生数理化·七年级数学人教版(2016年8期)2016-12-07
中学生数理化·七年级数学人教版(2016年7期)2016-12-07
小品文选刊(2016年17期)2016-12-06
读写算·高年级(2009年8期)2009-08-12
中学生数理化·八年级数学人教版(2008年2期)2008-10-14
中学生数理化·八年级数学华师大版(2008年4期)2008-09-05

