如何在小学数学教学中巧用“转化法”
郑小霞

摘 要 曹冲称象的故事发生在三国时期,时至今日,上千年过去了,但故事仍然被人津津乐道,多少人被曹冲的年少聪慧所折服,被故事所蕴含的思想所启迪。曹冲为什么聪明?那是因为他掌握了数学中的转换方法,大象称不了,就去称石头。
关键词 小学数学;转化法
中图分类号:G622 文献标识码:A 文章编号:1002-7661(2020)06-0153-01
在小学数学教学中,常常会遇到一些用“常规”方法无法解决的问题,这时我们也可以学习曹冲,可以借鉴曹冲称象的方法,把原来的貌似困难、无法下手的问题,转化为另一种自己熟悉并用此解决过问题的方法加以解决,这种解决问题的方法就是“转化法”。转化法是解决数学问题的一种常用方法,必须引导学生熟练掌握。
一、在计算教学中巧用“转化法”
在式题的计算中,换个角度,灵活转化原来的算式,可以使复杂的计算简便化。
(一)教师在教学“一个数除以小数”时,可以根据“被除数和除数同时扩大相同的倍数商不变的性质”,把除数是小数的除法转化成已学过的除数是整数的除法。如:
38.42÷3.842=38420÷3842=10
(二)连续除法,可以运用除法的性质,即
a÷b÷c=a÷(b×c),将较为复杂的难题转换为口算题。如,
4.32÷0.8÷1.25
=4.32÷(0.8×1.25)
=4.32÷1
=4.32
(三)可以利用乘法分配律的逆运算式,将求几个因式的和的形式转换成较为简单的运算。即ab+ac+ad=a(b+c+d)。如,
4.13×78﹢41.3×1.2﹢41.3
=4.13×78+4.13×12+4.13×10
=4.13×(78+12+10)
=4.13×100
=413
二、在数的大小比较中巧用“转化法”
在比较数的大小时,亦可以采用转化法,从而出现多种解法。
例如,比较两个异分母分数的大小时,可尝试以下方法:
1.化作同分母分数比较。
2.化作同分子分数比较。
3.化作小数比较。
三、转化法在求未知数中的应用
小学数学中出现的未知数问题,一般都是一元一次方程,解一元一次方程的主要理论依据,就是加、减、乘、除法各部分间的关系。利用这些关系及时转化问题,是小学数学解方程的关键。
例,解方程52-6x=16,学生直接计算是不行的,只有先将6x看作一个减数,利用减法中减数等于被减数减差的关系,转化成6x=52-16,先求出6x的值,再利用因数等于积除另一个因数的关系,求出x=6。
四、在几何初步知识教学中巧用“转化法”
小学几何图形、公式、定理,比较抽象难懂,适时运用转化思想,可以使复杂的问题简单化,使抽象的问题具体化。
例如,在探寻三角形的面积、圆的面积的计算方法时,学生们总是把新的图形经过剪、拼“转化”成已经学过的图形来推导出新的图形面积公式。对于许多组合图形,也可以采取旋转、平移、分割、拼合等办法把它转化成简单图形。
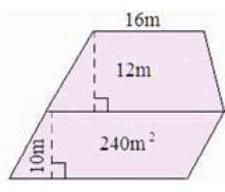
如,一块稻田的形状如上图,它的面积是多少?
五、在解决问题中巧用“转化法”
解决问题是数学教学的重點,也是大多数学生数学学习的难点,有些题目数量关系复杂,文字表述抽象,学生很难理解,个别题目稍有变化,学生就更加疑惑难懂,茫然不知所措。然而,在教学过程中,引导学生从抽象的文字表述中提取关键数据,发现规律,再将数据依据规律转化成线段图加以呈现,学生就会一目了然,顿时清楚明白,起到事半功倍的效果。
例如:学校图书馆新购一批故事书和科技书,其中故事书是科技书的3倍。已知故事书比科技书多8本,科技书和故事书各有多少本?教师可以把题中的数量关系转化成如下线段图,呈现在学生面前,这个问题就会迅速得到解决。
科技书:
故事书:
则,科技书=8÷(3-1)或者故事书=8÷2×3
为了进一步提升学生的数学思维能力,教师还可以让学生根据此线段图进行拓展训练,引导学生提出其它数学问题。如,两种书一共有多少本?科技书比故事书少了多少本?
总之,转化思想作为一种重要的数学思想,在解决问题中会经常用到,“授之以鱼,不如授之以渔。”在数学教学中,教师要不断强化转化思维的训练,努力提高学生解决问题的能力。
参考文献:
[1]廖克祥.农村小学数学学困生的成因及转化方法[J].小学教学参考,2013(3):38-39.

