带网损修正项的微电网线性化最优潮流

(广西大学电气工程学院， 广西南宁530004)

0 引言

微电网(microgrid, MG)是由分布式电源(distributed generation, DG)和负载组成的配电网络。MG中一次能源与电力网络中的能量交互通常以电压源逆变器作为接口,为确保系统的频率稳定、电压稳定、功率平衡和经济运行，各逆变器需要通过多种控制方法来协调运行[1]。为了应对这些挑战，学术界提出了分层控制框架作为微电网控制设计的标准[2-3]。

标准的分层控制框架共存在三个层次，具有不同时间尺度与优先级的控制。最底层为一次控制，它的目的是维持微电网稳定同时合理分配功率，一般由依赖本地信息的下垂控制来完成[4]。二次控制通过逆变器之间的分布式通信来调节一次控制的稳态误差[5]。一次控制和二次控制的运行点一般由可以观测网路全局信息的三次控制来进行调度。这一调度问题可以通过OPF来进行建模，以保证MG在满足运行约束的同时达到效益最大化[6-8]。

OPF问题是以潮流方程作为等式约束，同时考虑运行参数上下限，求解使得目标函数最小化的电力系统稳态运行点的数学规划问题[9]。微电网的潮流方程描绘了微电网在稳态运行中各节点物理量之间的非线性关系，是微电网稳态分析的基础。针对微网的非线性OPF问题，利用现代内点法直接求解，可得到一个局部最优解[10]。在此基础上，又提出了线性锥松弛的方法，如二阶锥规划[11]、半定规划[12]、半定规划与非线性规划[13]等。这些方法虽然理论上得到一个全局最优解，但是以它作为等式约束的最优潮流问题求解效率不高，无法应用于实时优化、滚动优化以及多微电网等计算量大、时效性要求高的场景，且存在特殊情况下的收敛性问题[14-15]。因此，根据应用场景对潮流方程进行高精度的线性近似再结合成熟的线性规划方法来进行求解，是工程与学术界持续关注的问题[16-18]。其中就有拟直流最优潮流[19-20]和半定规划的拟直流最优潮流[21]，即在类直流潮流模型的基础上引入修正因子对方程进行修正，但是这些文献的修正因子并不适用于分层控制下的微电网潮流计算，所建立的潮流方程也没有突显微电网潮流的特点。

根据定义，微电网属于低压配电系统，因此，文献[22-24]采用了经典的LinDistFlow模型[25]。然而，LinDistFlow要求网络拓扑是辐射状的，且无法建模电压相角，文献[26]提出了新的潮流方程线性近似模型，克服了LinDistFlow的上述缺陷。文献[27]在不同的坐标系下进一步分析了这一模型的精确性与适用范围，文献[28]将文献[26]和文献[27]中的线性化潮流模型应用到基于最优潮流的光伏调度问题中。文献[29]提出了考虑PV节点的线性化潮流模型，同时分析了与文献[26]在配电网应用上的等价性。然而，现有线性化潮流模型都是无损模型，即没有建模线路损耗对节点功率的影响，因此所得结果在网损较高时有较大的误差[28]。

针对上述问题，本文根据微电网的分层控制结构，充分考虑目标函数、网损以及分配因子之间的相关性，提出了一种带网损修正项的潮流方程线性近似，并建立带网损修正项的微电网线性化最优潮流模型。在IEEE-30、235、875这3个标准系统上，将本文模型与非线性最优潮流模型以及两个线性最优潮流进行仿真对比，证明该模型较现有近似模型有着更高的精确性，且保持了线性规划模型的在数值计算中的高效性和鲁棒性。

1 微电网潮流问题的建模

考虑节点数为N、支路数为L的微电网系统，定义集合N:={1,…,N}为它的节点集；它的子集NG和NL分别为可调度电源节点和负荷节点集，集合的势分别为NG和NL；⊆N×N为微电网支路集。当网络中不存在孤立节点时，微电网可以被描述为一个无向连通图G(N,)。当节点i与j相连时，支路{i,j}∈的串联导纳为yij=yji∈。由已知的网络拓扑与线路参数，可生成微电网的节点导纳矩阵Y∈N×N，其第i行、第j列的分量为Yij，计算公式如下：

(1)

其实部和虚部分别为节点电导和电纳矩阵Re{Y}=G，Im{Y}=B。低压电力系统中，由于线路较短，其并联导纳往往可以忽略不计[31]，即yii=0。此时Y为图G(N,L)的加权拉普拉斯矩阵，其零空间由各分量为1的N维列向量1所张成[32]，因此有:

Y1=1TY=O,

(2)

其中O各分量为0的N维列向量。

在N维复向量空间中，微电网的潮流方程可以写作如下形式：

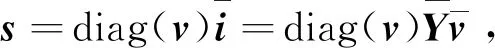
(3)

其中，v=[V1,…,VN]T∈N和i=[I1,…,IN]T∈N分别为各节点的电压相量和电流相量所构成的复向量；以及分别为其所对应变量的共轭向量；s=[S1,…,SN]T∈N为节点注入复功率向量，各分量为

2 带网损修正项的微电网线性化潮流方程

为满足用户对于电能质量的需求，微电网在正常运行状态下各节点电压幅值趋近于基准值；另外，由于低压系统线路短，阻抗较低，功率输送造成的电压相位差较小。利用上述特点，将电压写作基准值附近复无穷小扰动的形式，即v=1N+Δv。将其代入式(3)，同时考虑式(2)，可得：

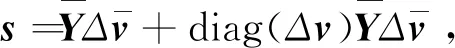
(4)

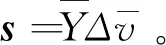
(5)

各节点注入功率相加，可以得到系统的总网损，即：

SL=1Ts。

(6)

将式(5)代入(6)，可得：

(7)

可见，式(5)所给出的线性近似没有考虑线路损耗对节点功率的影响，所得到的结果在网损影响较重的条件下会存在较大误差。为解决这一问题，本文对非线性项进行进一步处理。将式(5)代入式(4)中非线性项，可得：

(8)

在一般的配电系统中，各并网逆变器一般采用PQ控制，功率为待求变量。而对于分层控制下的微电网，各可调度电源之间会根据各自的控制参数进行自动功率分配。在功率分配参数已知的条件下，可以对给定负荷条件下的逆变器输出功率进行预估计。学术界已提出了一些功率分配控制方法[32-33]，虽然具体实施方式不同，但目标基本一致，即实现功率按比例分配。

(9)

(10)

(11)

式中，PGi，QGi和npi，nqi分别为可调度电源节点i的有功、无功输出功率和有功、无功分配因子；PLk，QLk分别为负荷节点k的负荷功率。假设功率分配控制与OPF目标相同，目标函数为C，可以通过等微增率准则求得各电源的npi和nqi

(12)

(13)

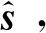
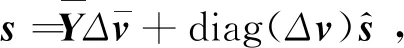
(14)

式中，第二项为网损修正项。

3 加入网损修正项的微电网最优潮流

最优潮流问题可根据不同的需要选择合适的目标函数，最典型的目标函数是发电费用函数。对于不同的电源，发电费用函数有不同的形式，但都可以利用分段线性函数进行拟合，精确度与段数呈正相关。对于分布式电源，由于其容量较小，一段线性近似往往可以满足精度要求[33]。因此，本文考虑如下发电费用函数作为目标函数。

(15)

式中，ci为电源i的单位功率电价。为防止设备过载，并使各节点电压满足运行要求，在优化目标函数的同时，需考虑如下基本的运行约束：

① DG有功功率约束

PGi,min≤PGi≤PGi,max。

(16)

② DG无功功率约束

QGi,min≤QGi≤QGi,max。

(17)

③ 节点电压幅值约束

|Vi|min≤|Vi|≤|Vi|max。

(18)

其中式(16)和式(17)都是线性不等式约束，不影响优化问题的基本性质。然而，式(18)属于非线性非凸不等式约束，它的存在会使最优潮流问题变为指数复杂度的非凸优化问题，为了避免这一困难，将式(18)在极坐标下展开：

(19)

由于ΔVi为远小于基准值1的扰动量，因此：

(1+Re(ΔVi))2≫Im(ΔVi)2。

(20)

约束(18)可近似为如下线性不等式约束：

|Vi|min≤1+Re(ΔVi)≤|Vi|max。

(21)

此时，结合带网损修正项的线性化潮流方程，可以得到如下线性规划形式的OPF：

(22)

4 算例分析

为了验证本文方法的性能，利用MATLAB 2016a编写程序，分别调用Gurobi和IPOPT优化软件包求解线性和非线性优化问题。测试系统的硬件环境为搭载Intel i5-4950 3.30 GHz的双核CPU，8G 内存，Win 10 64bit操作系统的台式计算机。

本文首先在规模较小的IEEE 33节点系统中加入可调度电源，将其变为微电网系统，以测试本文所提出方法的精确性，并与文献[24]和文献[28]中方法以及原非线性模型进行对比分析。然后，将模型应用于69、135和874节点系统，分析在系统规模较大的情况下线性近似算法的精确性和计算效率。

4.1 基于IEEE 33节点的微电网算例分析

IEEE 33节点系统[25]的拓扑图如图1，本文考虑一般的环网拓扑，闭合了所有联络开关，并在其中加入了可调度电源，位置、容量以及单价见表1，其中，节点1，15，30为容量较大的可调度电源,容量分别为2 000、1 600、1 000 kVA，最小功率因数为0.8，假设容量小的可调度电源价格更高；其他节点接入的电源为小容量可再生能源，额定功率分别为200、300 kW，假设它们的功率值由超短期负荷预测提供。

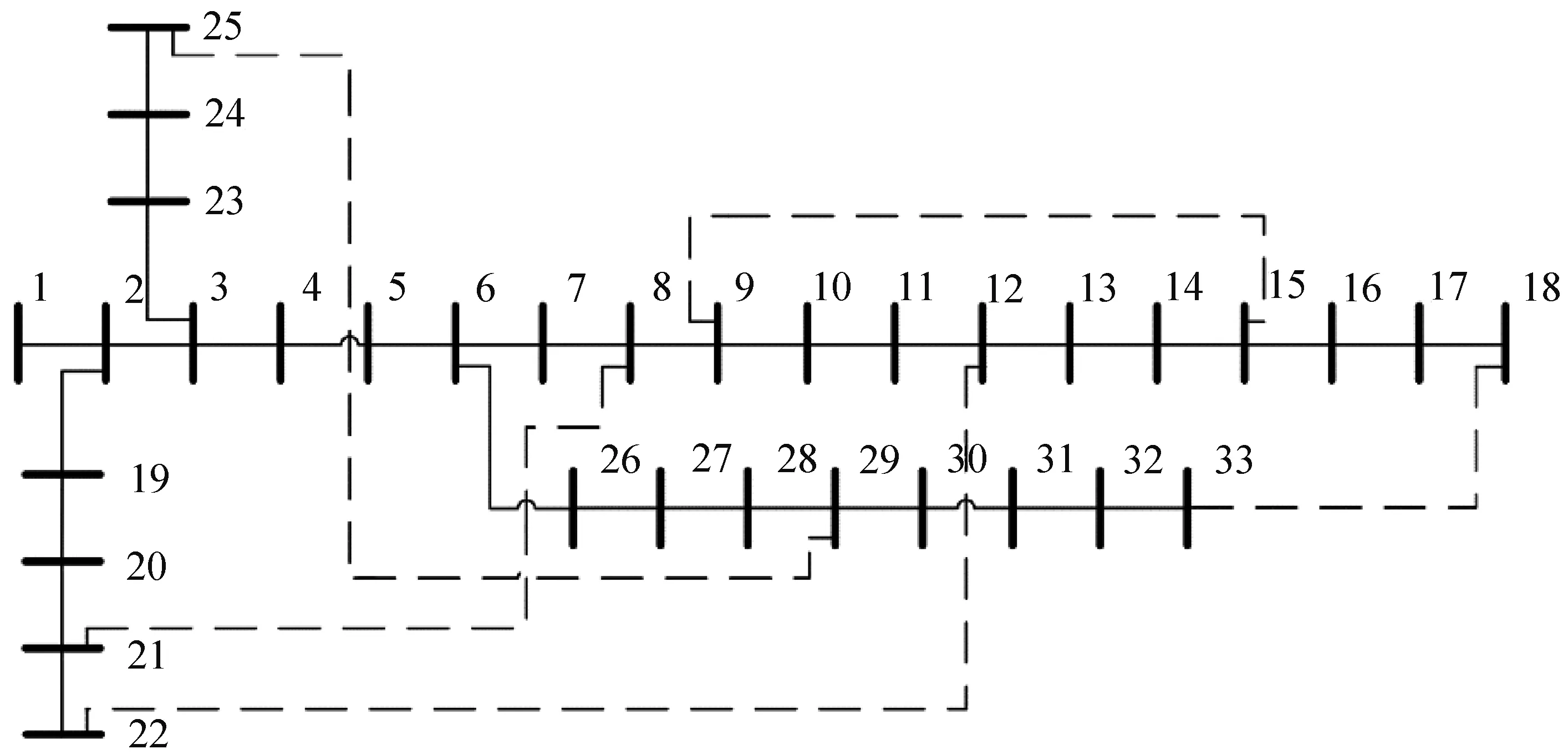
图1 IEEE 33节点网络拓扑Tab.1 Network topology of IEEE 33 system

为了验证本文OPF方法的精确性，在33节点微电网测试系统上分别计算非线性OPF、文献[24]中基于LinDistFlow的方法、文献[28]中的方法以及本文方法，所求得的结果见表2。在正常工况下，四种方法所得的结果基本一致，然而，由于文献[24]和[28]中的方法没有对节点功率与线路损耗之间的关系进行建模，各电源的功率之和等于负荷总功率，所得结果存在与总网损相当的误差。本文方法由于加入了网损修正项，网络损耗由价格次低的PG15所补偿，因此由网损所造成的误差大幅下降。

表1 33节点微电网中电源的位置与参数Tab.1 Placement and parameter of power sources in 33-node microgrid

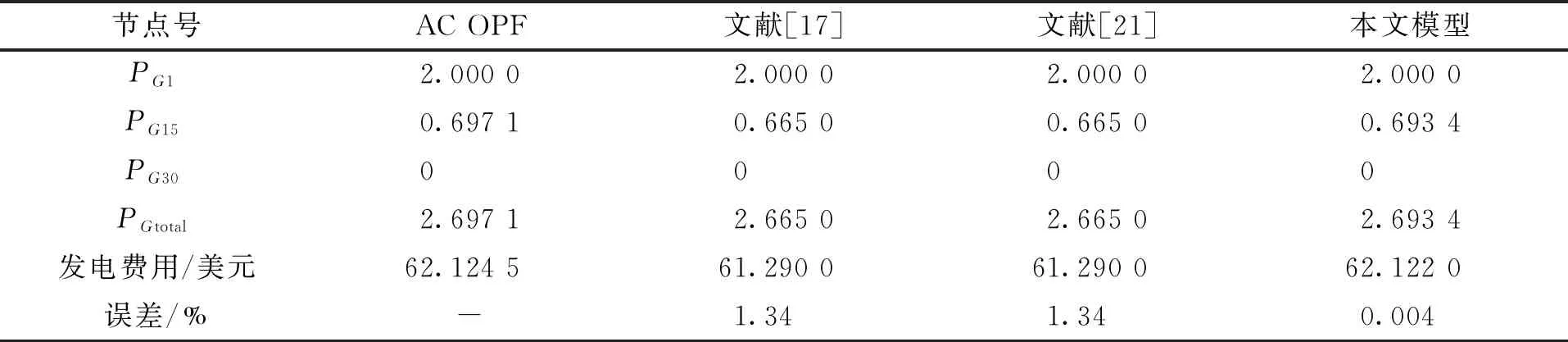
表2 33节点微电网中不同最优潮流所得结果对比Tab.2 Comparation of different OPF solutions in 33-node microgrid

4.2 135和874节点较大规模微电网算例分析

为了验证所提出模型的计算效率，本文在较大规模的135和874节点配电系统上进行算例分析，系统参数见文献[34]和[35]。将135和874节点配电系统与IEEE 33节点系统做出同样的处理，闭合所有联络开关形成环状拓扑，同时在不同节点分散地接入大量DG，容量和接入位置如表3所示。

在33、135以及874节点规模的微电网系统上，分别利用优化求解器计算非线性AC OPF与本文方法，所得目标值与求解时间见表4，其中ε是OPF目标值的相对误差。在较小的33节点系统上，本文方法计算时间与传统方法无差距较小，但随着系统规模增加，基于线性规划的本文方法逐渐凸显出计算效率上的优势，计算速度基本是传统方法的十倍左右。另外，由于本文加入了网损补偿，潮流方程的精确性的提升使得计算误差一直保持在非常小的范围内。

表3 35和874节点系统中DG接入的容量和位置Tab.3 capacity and location of DG integrated into 135 and 874 node systems

表4 本文方法与AC OPF计算效率比较Tab.4 comparation of computational efficiency of proposed method and AC OPF

5 结论

本文首先针对分层控制架构下的微电网提出了一种新的线性化潮流模型，该模型无需假设辐射状拓扑、同时考虑了电压幅值和相角、而且通过对下层功率均分控制的稳态建模，加入了适用于微电网的网损修正项。然后，基于所提出的潮流模型，考虑系统节点电压和设备容量约束，建立了以运行费用最小化为目标的线性规划形式的微电网OPF，可以利用成熟的商业优化软件求解。算例分析表明，所提出的方法与现有的线性化方法相比，由于考虑了微电网中网损与节点功率之间的关系，大幅降低了网损带来的近似误差，具有更高的精确性。与传统的非线性AC OPF相比，本文方法在保持高度精确性的同时，在较大规模的系统上大幅提升了计算速度。