含有时滞的倒向重随机控制系统最大值原理

许 洁, 吕显瑞

(1.吉林化工学院 理学院, 吉林 吉林 132022; 2.吉林大学 数学学院, 长春 130012)

目前, 关于时滞问题的研究已有很多结果[1-14].Huang等[5]探讨了一类含有时滞的正倒向线性二次随机系统, 给出了最优控制的显示表达式.Peng等[6]讨论了一类被称为超前倒向随机微分方程的新型倒向随机微分方程, 为解决随机时滞问题提供了一种新思路; Chen等[7]利用该类方程对倒向随机系统的时滞问题进行了更深入研究, 推导出对应系统的最大值原理, 完整刻画了时滞系统最优控制所满足的必要条件, 并将其应用到消费生产模型, 得出了最优消费率的显示表达式； Li等[8]研究了一类含有时滞和Levy过程的超前正倒向随机系统的最大值原理, 并对带有时滞和Levy过程的线性二次最优控制问题的最优反馈控制形式进行了探索[9].受上述工作的启发, 本文讨论时滞系统中所有状态变量和控制变量均含有时滞的情形, 通过引入对应系统的超前倒向重随机微分方程作为其伴随方程, 给出不同时滞问题最优控制满足的必要条件, 即时滞系统的最大值原理.本文的结果推广了仅单变量含有时滞的结果[10]和仅状态变量含有时滞的结果[11].

1 预备知识

设(Ω,F,P)为概率空间, {W(t): 0≤t≤T}和{B(t): 0≤t≤T}是定义在(Ω,F,P)上, 取值于m中两个相互独立的标准布朗运动, 其中关于{W(t)}是正向的It积分, 关于{B(t)}是倒向的It积分.设N表示F的所有P零测集.定义n)表示所有满足的Ft可测随机过程φ(t)的集合.定义凸集合U⊂k为

考虑时滞倒向重随机系统：

(1)

其中:f:Ω×[0,T]×n×n×n×m×n×m×k×k→n;g:Ω×[0,T]×n×n×n×m×n×m×k×k→n×d.为方便, 记xδ(t)=x(t-δ),yδ(t)=y(t-δ),uδ(t)=u(t-δ).目标泛函

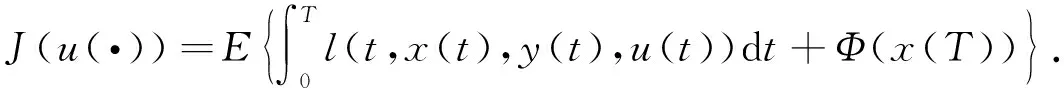
(2)

本文的最优控制问题就是在U[0,T]中找到最优控制u*(·), 使得

(3)

对应的(x*(·),y*(·),u*(·))称为最优三元组.假设条件如下：

(H1) 假设f和g是关于x,xδ,y,yδ,u,uδ连续可微的函数, 且其导数有界;

(H2) 假设存在正数c, 使得对所有的t∈[0,T],x,x′∈n,y,y′∈n×m,ξ,ξ′∈n,η,η′∈n×m, 有

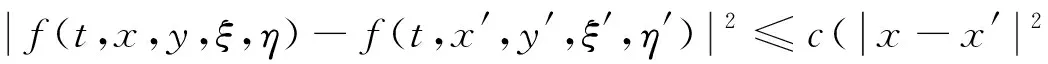
(H3) 假设存在正数c和α, 使得对所有的t∈[0,T],x,x′∈n,y,y′∈n×m,ξ,ξ′∈n,η,η′∈n×m, 有

设u*(·)是系统对应的最优控制, 则对任意的v(·)∈U, 设uε(·)=u*(·)+ε(v(·)-u*(·))=(1-ε)u*(·)+εv(·).为方便, 记v(t)-u*(t)为v(t).在控制域U是凸集的假设条件下, 显然uε(·)也属于U.由文献[11]中引理1知, 系统的状态方程(1)存在唯一解.

设(x*(·),y*(·))和(xε(·),yε(·))分别是方程(1)对应控制u*(·)和uε(·)的解.为方便, 用φx,φxδ,φy,φyδ,φu,φuδ分别表示φ对(x,xδ,y,yδ,u,uδ)的偏导数, 其中φ可以取f,g,l.考虑差分方程：

2 主要结果

首先给出该时滞系统对应的变分不等式：

定理1设条件(H1)成立, 则有

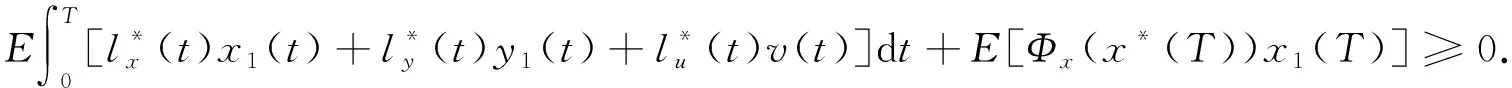
(4)

证明： 由于u*(·)是系统对应的最优控制, 因此对任意v(·)∈U,uε(·)∈U, 可得

J(uε(·))-J(u*(·))≥0,

(5)

则

从而有

(7)

由

及uε(t)=u*(t)+εv(t), 又由文献[12]中引理3.3, 直接可得

则变分不等式可写成

(9)

证毕.

对t∈[0,T]及任意v(·)∈U[0,T], 定义Hamilton函数

(t,x(t),xδ(t),y(t),yδ(t),u(t),uδ(t),p(t),q(t))∈[0,T]×n×n×n×m×n×m×k×k×n×n×d.

定理2设(x*(·),y*(·),u*(·))是系统(1)-(3)的最优三元组, 如果时滞变量δ充分小, 且存在唯一的Ft适应解, 满足下列伴随方程:

则有

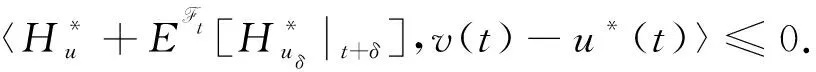
(12)

证明： 伴随方程(11)是一类新型的超前倒向重随机微分方程, 文献[13]中定理3.2和文献[14]中定理2.4给出了其解的存在唯一性证明, 这里不再重复.

对〈p(t),x1(t)〉应用It公式并取期望可得

本工程位于陕西省汉中市石马路与傥骆路十字东北侧地块，连通西成高铁汉中站，交通十分便利。本工程总建筑面积155 536m2，地上建筑面积 97 728m2，含东、西翼塔楼（22 层，高100m）和裙房（3～5 层，最高 38m），包括百货、超市、电影院、兼具餐饮功能。地下建筑面积57 808m2，为2层地下室。各单体之间在地上均设缝相互分开独立，2层地下室联成一体，结构模型如图1所示。

利用系统的初始条件及终端条件可得

即

(14)

类似可得

式(13)可以写成

即

(20)

由变分不等式和Hamilton函数的定义可得

(21)

对任意0≤t≤T和v∈U[0,T], 有

令ε→0, 有

(23)

由v(t)的定义可得

(24)

对任意v(t)∈U[0,T], 设ν是一个确定的元素,A是σ-代数Ft中的任意一个元素, 且

ω(t)=ν1A+u(t)1Ac,

(25)

ω(·)是一个可容控制, 则不等式(24)可以写成

(26)

对所有的A∈Ft, 可推得

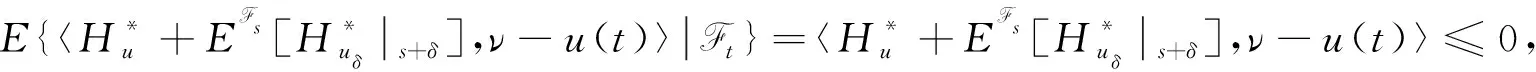
(27)

证毕.