2020年全国高考文科数学模拟试题

高慧明

1.已知集合A={1， 2， 3}，B={x | （x+1）（x-2）≤0}，则A∩B 等于（）

A.{1}

B.{1， 2}

C.{0， 1， 2， 3}

D.{-1， 0， 1， 2， 3}

2.已知复数z在复平面内对应点是（1， -2），i为虚数单位，则■=（）

A. -1-iB. 1+iC. 1-■iD. 1+■i

3.命题“？坌x∈R，x3-x2+1≤0”的否定是（）

A. 不存在x0∈R，x03-x02+1≤0

B. ？埚x0∈R，x03-x02+1≥0

C. ？埚x0∈R，x03-x02+1>0

D. ？坌x∈R，x3-x2+1>0

4.已知向量■=（4， -1），■=（-5， 2），且（■+■）∥（m■-■），则实数m=（）

A. 1B. -1 C. ■D. -■

5.已知a=21.2，b=（■）-0.8，c=2log52，则a， b， c的大小关系为（）

A. c

6.数学名著《算学启蒙》中有关于“松竹并生”的问题：松长四尺，竹长两尺，松日自半，竹日自倍，松竹何日而长等. 如图，是源于其思想的一个程序框图. 若输入的a，b分别为8，2，则输出的 n=（）

A. 2B. 3

C. 4D. 5

7.在△ABC中，角A， B， C的对边分别为a， b， c，若A=30°，b2=2ac，则■=（）

A. 1B. 2

C. ■  D. ■

8.在区间[-■，■]上随机取一个数x，则sin2x的值介于0到■之间的概率为（）

A. ■  B. ■C. ■D. ■

9. 已知直线y=kx（k≠0）与双曲线■-■=1（a>0，b>0）交于A，B两点，以AB为直径的圆恰好经过双曲线的右焦点F，若△ABF的面积为4a2，则双曲线的离心率为（）

A. ■ B. ■C. 2 D. ■

10. 设函数f（x）的定义域D，如果存在正实数m，使得对任意x∈D，都有f（x+m）>f（x），则称f（x）为D上的“m型增函数”，已知函数f（x）是定义在R上的奇函数，且当x>0时，f（x）=x-a-a（a∈R）. 若f（x）为R上的“20型增函数”，则实数a的取值范围是（）

A. a>0 B. a<5 C. a<10 D. a<20

11. 已知过球面上三点A， B， C的截面到球心距离等于球半径的一半，且AC=BC=6，AB=4，则球面面积为（）

A. 42？仔 B. 48？仔C. 54？仔D. 60？仔

12. 已知直线l ∶ y=-2x-m（m>0）与圆C ∶x2+y2-2x-2y-23=0，直线l与圆C相交于不同两点M，N. 若■≤2■+■，则m的取值范围是（）

A.[■， 5 ） B.[2， 5■-3）

C.（5， 5■） D.（■， 2）

13. 函数y=■的图像在x=1处的切线方程是_________.

14. 已知x， y满足不等式组x≥1，x-2y+3≥0，y≥x，则z=x+y的最小值等于__________.

15. 若f（x）=lgx，x>0ax+b，x≤0 f（0）=2，f（-1）=4，则f（f（-2））=___________.

16. 如图所示，平面BCC1B1⊥平面ABC，ABC=120°，四边形BCC1B1为正方形，且AB=BC=2，则异面直线BC1与AC所成角的余弦值为__________.

17. 已知{an}是等差数列， {bn}是等比数列，且b2=2，b5=16，a1=2b1，a3=b4 .

（1）求{bn}的通项公式;

（2）设cn=an+bn，求数列{cn}的前n项和.

18. 已知某单位全体员工年龄频率分布表为：

经统计，该单位35岁以下的青年职工中，男职工和女职工人数相等，且男职工的年龄频率分布直方图和如下：

（1）求a;

（2）求该单位男女职工的比例;

（3）若从年龄在[25， 30）岁的职工中随机抽取两人参加某项活动，求恰好抽取一名男职工和一名女职工的概率.

19. 三棱柱ABC-A1B1C1被平面A1B1C截去一部分后得到如图所示几何体，BB1⊥平面ABC，∠ABC=90°，BC=BB1，E为棱B1C上的动点（不包含端点），平面ABE交A1C于点F.

（1）求证：AB⊥平面B1BC;

（2）求证：EF∥AB;

（3）试问是否存在点E，使得平面ABE⊥平面A1B1C，并说明理由.

20. 已知点M（x0， y0）为椭圆C ∶■+y2=1上任意一点，直线l ∶  x0x+2y0y=2与圆（x-1）2+y2=6交于A， B兩点，点F为椭圆C的左焦点.

（1）求椭圆C的离心率及左焦点F的坐标;

（2）求证：直线l与椭圆C相切;

（3）判断∠AFB是否为定值，并说明理由.

21. 已知函数f（x）=2xlnx-x-■+2.

（1）求曲线y=f（x）在点（1，f（1））处的切线方程;

（2）求证：（x-1）f（x）≥0.

22. [选修4—4：坐标系与参数方程]

在直角坐标系xOy中，直线l的参数方程为x=2+■t，y=2■+■t（t为参数）. 曲线C的方程为x2-2x+y2=0. 以坐标原点O为极点，x轴正半轴为极轴建立极坐标系.

（1）求直线l的普通方程与曲线C的极坐标方程;

（2）直线m ∶  x-y+2■-2=0与直线l交于点A，点B是曲线C上一点，求△AOB面积的最大值.

23. 已知函数f（x）=x-2+x+a，a∈R.

（1）若a=1，解不等式f（x）+x>0;

（2）对任意x∈R，f（x）≤3恒成立，求实数a的取值范围.

答案和解析

1. 答案及解析：

答案：B

解析：∵集合A={1， 2， 3}，B={x│（x+1）（x-2）≤0}={x│-1≤x≤2}，

∴ A∩B={1， 2}. 故选B.

2. 答案及解析：

答案：D

解析：■=■=1+■i，故选D.

3. 答案及解析：

答案：C

解析：由全称命题的否定是特称命题可得命题？坌x∈R，x3-x2+1≤0的否定是“？埚x0∈R，x03-x02+1>0”，故选C.

4. 答案及解析：

答案：B

解析：易知■+■=（-1，1），m■-■=m（4，-1）-（-5，2）=（4m+5，-m-2），因为（■+■）∥（m■-■），所以（-1）×（-m-2）-1×（4m+5）=0，解得：m=-1，故选B.

5. 答案及解析：

答案：A

解析：∵ a=21.2>2，b=（■）-0.8=20.8<21=2，c=log 5 4

∴ c

6. 答案及解析：

答案：D

解析：输入的a， b分别为8， 2， n=1，

第一次执行循环体后a=12，b=4不满足退出循环的条件，

第二次执行循环体后n=2， a=18， b=8，不满足退出循环的条件，

第三次执行循环体后n=3， a=27， b=16，不满足退出循环的条件，

第四次执行循环体后n=4， a=■， b=32，不满足退出循环的条件，

第五次执行循环体后n=5， a=■， b=64，满足退出循环的条件，

故输出的n=5，故选D.

7. 答案及解析：

答案：A

解析：因为b2=2ac，由正弦定理，得sin2B=2sinAsinC=2sin30°sinC=sinC，所以■=■=1，

故选A.

8. 答案及解析：

答案：D

解析：所有的基本事件构成的区间长度为■-（-■）=■，由0≤sin2x≤■，解得：0≤2x≤■，则0≤x≤■，所以由几何概型的概率公式得sin2x的值介于0到■之间的概率为P=■=■，

故選：D.

9. 答案及解析：

答案：D

解析：由题意可得图像如图所示：F′为双曲线的左焦点.

∵ AB为圆的直径，

∴∠AFB=90°.

根据双曲线、圆的对称性可知：四边形AFBF′为矩形，

∴ S△ABF =■SAFBF ′=S△FBF ′.

又S△FBF ′=■=b2=4a2，可得：c2=5a2.

∴ e2=5？圯e=■. 故选D.

10. 答案及解析：

答案：B

解析：若a≤0：当x>0时，f（x）=x-a-a=x= x，

又∵f（x）是定义在R上的奇函数，∴f（x）=x，符合题意;

若a>0，当x>0时，f（x）=x-a-a=-x， 0

又∵f（x）是定义在R上的奇函数，根据题意可知f（x+20）>f（x）对于任意x∈R恒成立，∴问题等价于将f（x）的图像向左平移20个单位后得到的新的函数f（x+20）图像恒在f（x）图像上方，可知4a<20，即0

11. 答案及解析：

答案：C

解析：如图，设球的半径为R，O′是△ABC的外心，外接圆半径为r，则OO′⊥面ABC. 在Rt△ACD中，cosA=■，则sinA=■.

在△ABC中，由正弦定理得■=2r，r=■■，△ABC外接圆的半径r=■=■R？圯R2=■，S=4？仔R2=54？仔. 故选：C.

12. 答案及解析：

答案：B

解析：圆C方程可化为：（x-1）2+（y-1）2=25？圯C（1，1），圆C半径r=5.

■≤2■+■=■2≤4■+■2，

即■2≤4■2+4■2+8■·■.

∴■2≤100+100+8■·■cos∠MCN

？圯■2≤100+100+200×■？圯■≤4■.

设圆心C到直线y=-2x-m的距离为d，

则2■=2■≤4■？圯m≥2.

又直线y=-2x-m与圆C相交，可得d

即■<5？圯m<5■-3.

综上所述：m∈[2， 5■-3）.

故选B.

13. 答案及解析：

答案：x-y-1=0

解析：y′=■，所以y′│x=1=1，又当x=1时，y=0，所以切线方程为y=x-1，

故答案为：x-y-1=0.

14. 答案及解析：

答案：2

解析：作出不等式组对应的平面区域如图：

由z=x+y，得y=-x+z，

平移直线y=-x+z，由图象知当直线经过点A时，直线y=-x+z的截距最小，

此时，z最小，

由x=1，y=x，得x=1，y=1，即A（1， 1），

此时，z=1+1=2，

故答案为：2.

15答案及解析：

答案：1

解析：f（0）=2，f（-1）=4？圯a0+b=2，a-1+b=4，解得a=■，b=1.

∴当x≤0时，f（x）=（■）x+1.

∴f（-2）=（■）-2+1=10？圯f（f（-2））=f（10）=lg10=1.

本题正确结果：1

16. 答案及解析：

答案：■

解析：由题目中的位置关系，可将原图补为如图所示的直四棱柱：

∵ BC1∥AD，

异面直线BC1与AC所成角即为直线AD与AC所成角∠DAC.

由余弦定理可得：AC2=AB2+BC2-2AB·BCcos∠ABC=4+4-8cos120°=12.

∴ AC=2■，又AD=CD=■=2■.

∴ cos∠DAC=■=■=■.

本题正确结果：■.

17. 答案及解析：

答案：

（1）设{bn}的公比为q.

因为b2=2，b5=16，所以q3=■=■=8，

所以q=2. b1=■=1，

所以bn=b1qn-1=2n-1（n=1， 2， 3，…）.

（2）由（1）知bn=2n-1，所以b1=1，b4=8.

设等差数列{an}的公差为d.

因为a1=2b1，a3=b4

所以a1=2，a3=a1+2d=8.

所以d=3.

所以an=3n-1.

因此cn=an+bn=3n-1+2n-1.

从而数列{an}的前项和：

Sn=2+5+…+（3n-1）+1+2+…+2n-1.

Cn=■+■

=■n2+■n+2n-1

18. 答案及解析：

答案：（1）由男职工的年龄频率分布直方图可得：

（a+0.01+0.04+0.08+0.025+0.025）×5=1.

所以a=0.02.

（2）该单位[25，35）岁职工共24人，由于[25，35）岁男女职工人数相等，所以[25，35）岁的男职工共12人.

由（1）知，男职工年龄在[25，35）岁的频率为0.15，

所以男职工共有■=80人，

所以女职工有140-80=60人，

所以男女比例为4 ∶ 3.

（3）由男职工的年龄频率分布直方图可得：男职工年龄在[25，30）岁的频率为0.05.

由（2）知，男职工共有80人，所以男职工年龄在[25，30）岁的有4人，分别记为A1， A2， A3， A4.

又全体员工年龄在[25，30）岁的有6人，所以女职工年龄在[25，30）岁的有2人，分别记为B1， B2.

从年龄在25～30岁的职工中随机抽取两人的结果共有（A1， A2），（A1， A3），（A1， A4），（A1， B1），（A1， B2），（A2， A3），（A2， A4），（A2， B1），（A2， B2），（A3， A4），（A3， B1），（A3， B2），（A4， B1），（A4， B2），（B1， B2）15种情况，

其中一男一女的有（A1， B1），（A1， B2），（A2， B1），（A2， B2），（A3， B1），（A3， B2），（A4， B1），（A4， B2） 8種情况，

所以恰好抽取一名男职工和一名女职工的概率为■.

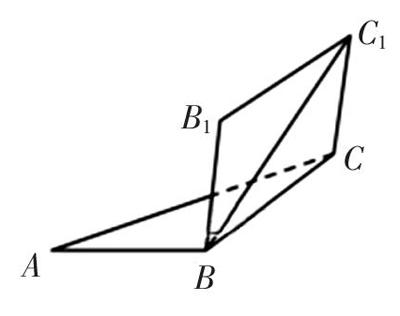
19. 答案及解析：

答案：（1）因为BB1⊥平面ABC，AB？奂平面ABC，

所以BB1⊥AB.

因为∠ABC=90°，

所以BC⊥AB.

因为BB1∩BC=B，B1B？奂平面B1BC，BC？奂平面B1BC，

所以AB⊥平面B1BC.

（2）在三棱柱ABC-A1B1C1中，AB∥A1B1.

因为AB？埭平面A1B1C，A1B1？奂平面A1B1C，

所以AB∥平面A1B1C.

因为AB？奂平面ABEF，平面ABEF∩平面A1B1C=EF，

所以EF∥AB.

（3）AB⊥BE.

因为AB∥A1B1，

所以BE⊥A1B1.

因为A1B1∩B1C=B1，

所以BE⊥平面A1B1C.

因为BE？奂平面ABE，

所以平面ABE⊥平面A1B1C.

20. 答案及解析：

答案：

（1）由题意a=■，b=1，c=■=1，

所以离心率e=■=■，左焦点F（-1，0）.

（2）由题知，■+y20=1，即x20+2y20=2.

当y0=0时直线l方程为x=■或x=-■，直线l与椭圆C相切.

当y0≠0时，由■+y2=1，x0 x+2y0 y=2，得（2y20+x20）x2-4x0 x+4-4y20=0，

即x2-2x0 x+2-2y20=0.

所以△=（-2x0）2-4（2-2y20）=4x20+8y20-8=0.

故直线l与椭圆C相切.

（3）设A（x1， y1），B（x2， y2），

当y0=0时，x1=x2，y1=-y2，x1=±■，

■·■=（x1+1）2-y21=（x1+1）2-6+（x1-1）2=2x21-4=0，

所以■⊥■，即∠AFB=90°.

当y0≠0时，由（x-1）2+y2=6，x0 x+2y0 y=2，得（y20+1）x2-2（2y20+x0）x+2-10y20=0，

则x1+x2=■，x1x2=■，

y1y2=■x1x2-■（x1+x2）+■=■.

因为■·■=（x1+1，y1）·（x2+1，y2）

=x1x2+x1+x2+1+y1y2

=■+■

=■=0.

所以■⊥■，∠AFB=90°.

故∠AFB为定值90°.

21. 答案及解析：

答案：（1）f（x）定义域为（0， +∞），f（1）=0.

f′（x）=2（1+lnx）-1+■=1+■+2lnx. f′（1）=2.

所以曲线y=f（x）在（1，f（1））处的切线方程为y-0=2（x-1）.

即y= 2x-2.

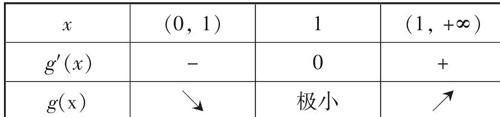
（2）记g（x）=1+■+2lnx.

g ′（x）=■-■=■.

由g ′（x）=0解得x=1.

g（x）与g ′（x）在区间（0， +∞）上的情况如下：

所以g（x）在x=1时取得最小值g（1）=2.

所以g（x）=1+■+2lnx≥2>0. 所以f ′（x）>0.

所以f（x）在（0，+∞）上单调递增.

又由f（1）=0知：

当00;

当x>1时，f（x）>0，x-1>0，所以（x-1）f （x）>0.

所以（x-1）f （x）≥0.

22. 答案及解析：

答案：（1）由x=2+■t得t=■（x-2）

代入y=2■+■t整理得：x-■y+4=0.

∴直线l的普通方程为x-■y+4=0.

又x= ？籽cos？兹，y= ？籽sin？兹，

曲线C的极坐标方程为？籽=2cos？兹.

（2）由x-y+2■-2=0，x-■y+4=0，得x=2，y=2■，

∴  A（2， 2■）.

设B（？籽，？兹），则？籽=2cos？兹.

∴△AOB的面积S=■OAOBsin∠AOB

=■4？籽sin（■-？兹）=4cos？兹sin（■-？茲）=2cos（2？兹+■）+■.

Smax=2+■.

23. 答案及解析：

答案：（1）当a=1时，f（x）+x=x-2-x+1+x，

①当x≤-1时，f（x）+ x = -x-2+x+1+x=-x+3>0，解得x>-3，

所以-3

②当-10，解得x<1，

所以-1

③当x≥2时，f（x）+x=（x-2）-（x+1）+x=x-3>0，解得x>3，

所以x>3.

所以不等式f（x）+x>0的解集为（-3，1）∪（3，+∞）.

（2）因为f（x）=x-2-x+a≤（x-2）-（x+a）=a+2，

所以f（x）max=a+2.

因为对任意x∈R，f（x）≤3恒成立，

所以a+2≤3，

所以-3≤a+2≤3，

所以-5≤a≤1.

所以实数的取值范围为[-5，1] .

责任编辑徐国坚