非线性非局部多孔介质方程在非线性边界条件下爆破时间的下界*

欧阳柏平， 刘炎

(1. 广东财经大学华商学院数据科学学院，广东 广州 511300； 2. 广东金融学院金融数学与统计学院, 广东 广州 510521)

在文[1]中，作者研究了如下的非线性非局部的多孔介质方程的爆破问题：

(1)

u(x,0)=f(x)≥0,x∈Ω

(2)

给出Robin边界条件：

(3)

其中Ω是R3中的一个有界凸区域，Δ代表拉普拉斯算子，▽ 代表梯度算子。∂Ω 是区域Ω的边界， 以及t*代表可能的爆破时间。作者得到当爆破发生时，(1)～(3)系统的爆破时间的下界。

在文[2]中，作者同样研究了在齐次狄利克雷边界条件下以及齐次牛曼边界条件下方程组(1)和(2)的爆破问题，得到了在两种边界条件下爆破解的爆破时间下界。方程(1) 是用来研究人口动力学的[3]。 在文[4]中，作者证明当p+q>m>1时只要初始值u0足够大，方程组(1)～(2)的解将会在有限时间内爆破。

很多文献研究了抛物方程在齐次狄利克雷边界条件下以及齐次牛曼边界条件下的解的爆破问题[5-12]，一些文献已经开始研究在Robin边界条件下解的爆破问题[13-14]。

在文[15-17]中，作者研究了非线性边界条件下的热方程的爆破问题。 到目前为止，我们还未发现有论文研究非线性边界条件下的非线性非局部多孔介质方程的解的爆破时间下界问题。从这点来看，本文所得到的结果是新且有趣的。

本文中，我们考虑方程组(1)～(2)满足如下非线性边界条件：

(4)

0≤g(ξ)≤k1ξ2+ms-m对于任意ξ>0

(5)

其中k1是一个正常数，s将会在式(10)中定义。

我们将研究方程组(1)～(2)在边界条件(4)～(5)下的解的爆破时间的下界。

1 几个重要的不等式

在后面证明中，将会用到如下几个重要不等式：

引理1 如果n1,n2,x1,x2都是正常数且x1,x2满足x1+x2=1，则对于任意非负函数u均有如下的Hölder 不等式：

(6)

引理2 对于任意非负函数u，以及任意的正常数m和s，我们有

(7)

证明有如下等式

div(u5msx)=3u5ms+5msw5ms-1(x·▽u)

(8)

对等式(8)两边积分可得

由散度定理可得

引理3 对于任意非负函数u，以及任意的正常数n，有

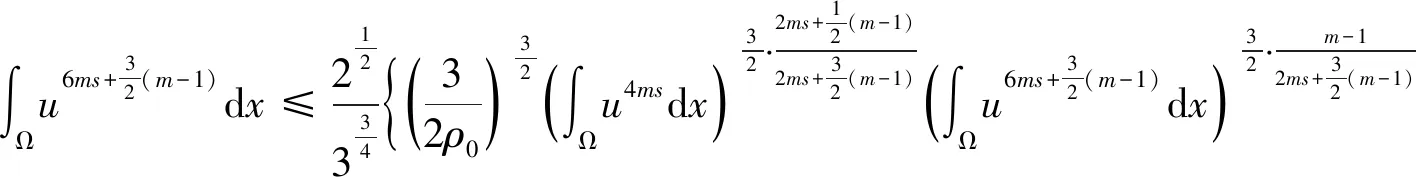
(9)

证明由文[8](2.16)或者文[16](4.10)可得

运用式(6)并取

以及

得到

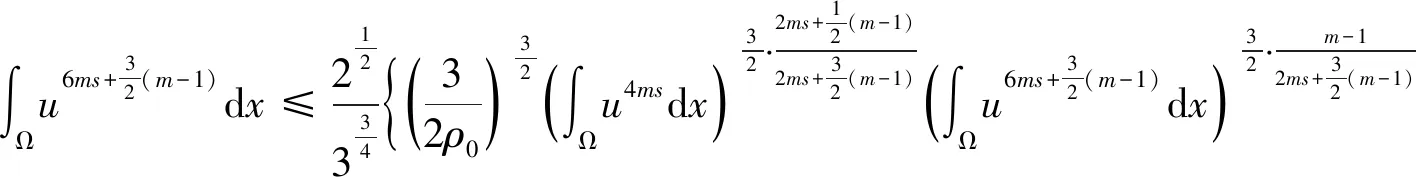
2 爆破时间的下界

定义如下的辅助函数：

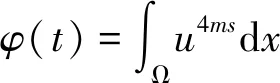
(10)

其中s=p+q-1

将建立如下的定理：

定理1 假设u(x,t)是问题(1)，(4) 以及(5) 在有界凸区域Ω的经典的非负解。假设p+q>m>1，则式(10)中定义的量满足微分不等式

(11)

由此可得爆破时间t*的下界为

(12)

其中k2,k3,k4,k5在后面定义的正常数。

接下来证明定理1。 首先对函数(10)求导数得

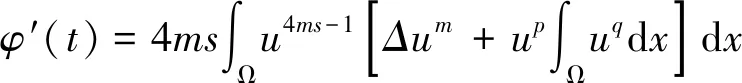
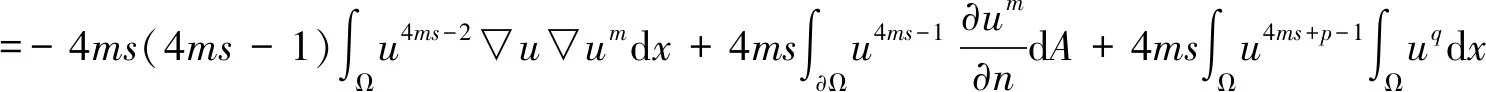
(13)

由式 (7)可得

(14)

应用式(6)并且选择

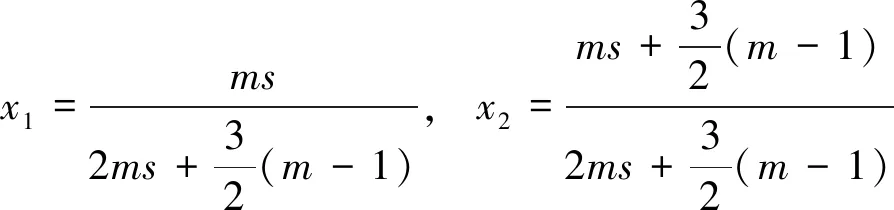
可得到

(15)

应用 Schwarz 不等式得

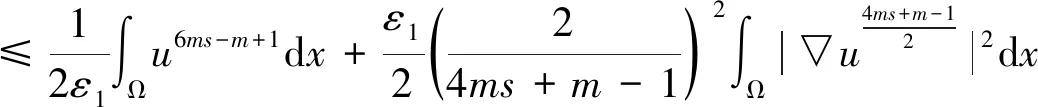
(16)

选择

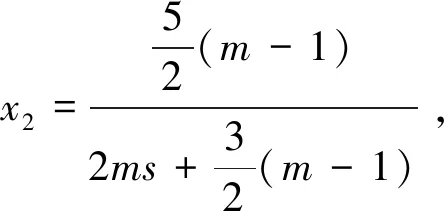
(17)

类似地，如果选择

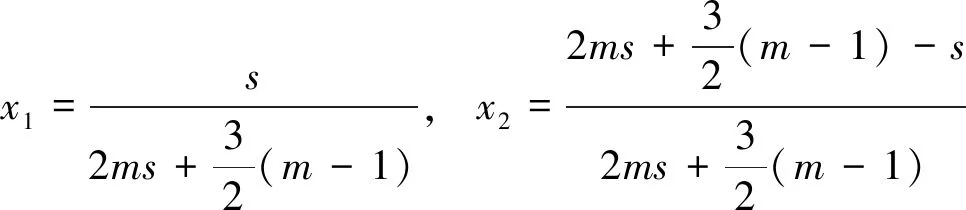
得到

(18)

联合式(14)～(18)，得到

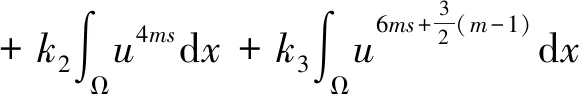
(19)

其中

运用式(9)，得到

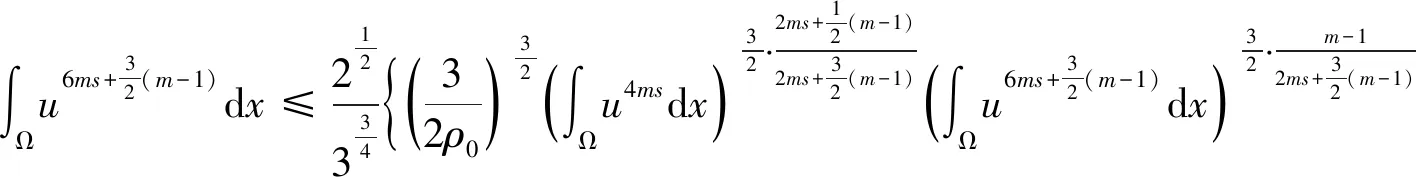
(20)

其中ε2，ε3和ε4都是后面会给出定义的正常数。

如果选择合适的ε2和ε4满足

将得到

(21)

其中

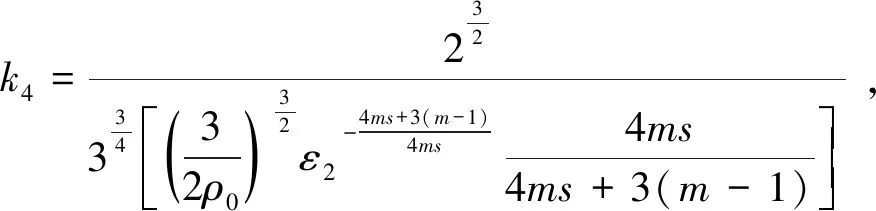
联合式(19)与式(21)可得

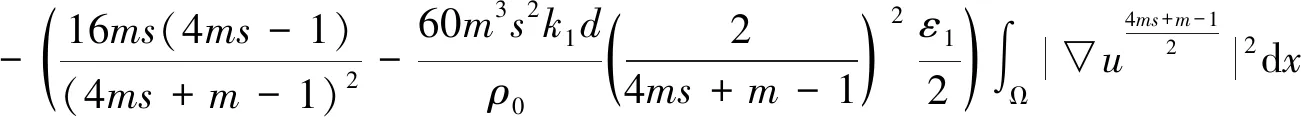
(22)

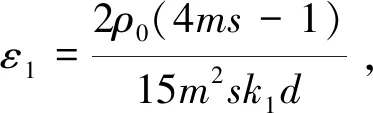
得到

(23)

也就是说

(24)

式(24) 可写作如下形式

(25)

对式(25)积分可得

(26)

得到定理需要证明的结论。