螺纹载荷分布计算方法研究及有限元分析*

颜庭梁,李家春

（贵州大学 机械工程学院，贵州 贵阳 550025）

0 引 言

众所周知，螺栓是机械基础件中应用最广泛的紧固件联接零件之一，螺栓具有较强的通用性、可靠性、互换性，已成为标准化零件。在螺栓承受重载时，由于螺纹结构的特点，极易从螺纹结合第一扣发生裂纹。随着循环载荷次数的增加，裂纹不断扩大，可能导致螺纹牙的断裂，极大影响了螺栓在重载机械上的可靠性。保证螺栓的可靠性就是保证机械系统的可靠性。因此，螺栓的设计与选择不当，会导致联接失效等故障出现，造成停机、停工、停产，甚至导致机毁人亡。

螺栓在受轴向载荷时，螺栓受拉发生轴向拉伸，从而使螺距增大，螺母受压发生轴向的压缩，使其螺距减少，因而产生了螺距差，导致了螺纹部分的应力集中[1]。在螺栓连接中，其应力集中主要分布在螺栓螺纹不完整处以及螺栓头部圆角位置。但是，螺纹啮合尾部的应力集中系数较大，因此，螺纹断裂通常发生在螺纹啮合的第一扣[2]。

我国的高速列车正处于高速发展阶段，制动盘作为高速列车制动系统的核心部件，对其性能要求很高。而螺栓作为高速列车制动盘最主要的标准件之一，起着紧固制动盘的作用。随着列车运行速度的提高，制动盘螺栓承受越来越大的载荷，因此，对于紧固件用螺栓的可靠性有着十分严格的要求。

现有螺栓螺纹的设计都是以经验设计为主，本文提出一种新的螺栓螺纹承载分布公式，为提高螺栓的可靠性与螺栓精确设计提供一定的参考。

1 现有的研究方法

现有的螺纹副载荷分布的研究方法主要包括：理论分析法、光弹冷冻应力实验法和有限元法。

1.1 螺纹副载荷分布的理论分析法

为解决螺纹牙载荷分布不均的问题，SOPWITH[3]与YAMAMOTO[4]将螺纹牙看作悬臂梁结构，对螺纹牙载荷进行了理论分析，从理论上得出了螺纹载荷分布不均的原因。

SOPWITH法得出的螺母径向任意截面的载荷为:

（1）

YAMAMOTO法得出的螺母径向任意截面的载荷与轴向载荷的比例为:

（2）

式中：x—距离螺母顶面的距离；θ—螺栓轴向力分布系数；λ—螺栓轴向力分布系数。

BRETL J L等[5]提出了单自由度的弹簧系统，建立了平衡方程，模拟螺纹联接中的负载位移。张鹏等[6]通过ANSYS分析了动载激励下的预紧螺栓轴向应力的分布特征，并采用YAMAMOTO法进行了验证，但未提出准确螺栓轴向应力分布公式。

徐静等[7]运用ANSYS对螺栓法兰连接结构应力进行了分析，得出了内测螺栓受到的影响较大，确认35CrMoA合金钢材作为螺栓法兰结构的整体材料符合使用要求。

1.2 螺纹副载荷分布的光弹冷冻应力实验法

通过光弹实验，可对螺纹载荷分布进行研究，采用环氧树脂材料进行螺栓建模[8-9]，对模型进行加载、应力冻结，制作成螺纹切片，在偏振光场下观察，利用透明材料（环氧树脂材料）在受力变形时产生光学各向异性的特点，可得到螺纹的应力状态和分布。

光弹实验可以得到螺纹副载荷分布结果。但是，由于切片制造工艺、加工与配合精度等原因，实验结果会出现一定误差。

1.3 螺纹副载荷分布的有限元分析法

陈海平等[10]建立了不同参数的螺栓二维模型，通过有限元法得出了螺纹承载比例的分布规律；ZHAO等[11]提出了一种三维简化模型的有限元分析方法，考察了螺纹副3种节点载荷分布情况；RIDONG L等[12]提出了一种新的非线性加载-卸载过程的收敛准则，采用有限元模型，根据收敛准则得出了轴向载荷和应力在螺纹中的分布对施加载荷的规律。

2 螺纹副载荷分布理论分析

2.1 螺纹副受力分析

由内外螺纹受力分析可得：

（1）轴向载荷会导致螺栓拉长和螺母的压缩；

（2）垂直于螺纹面的力F/cosα，使螺栓和螺母的螺纹发生了变形（螺纹牙的弯曲变形和剪切变形）；

（3）径向力使螺栓螺纹径向压缩，使螺母发生整体的径向膨胀，也可能存在径向的应变。

在通常的螺纹牙受力分析计算时，假设为载荷施加在中径d2处的载荷，若将旋合状态下的螺栓与螺母沿旋合线展开，其结构可以看作类似于斜齿轮双齿啮合的情况（啮合线为螺纹螺旋线），采用类齿轮齿牙弹性变形分析方法即可对螺纹变形进行分析。

2.2 螺纹牙的弹性变形

螺纹牙的弹性变形如图1所示。

梯形部分的弯曲变形为：

（3）

剪切变形为：

（4）

螺纹牙牙根部分倾斜产生的变形为：

（5）

接触变形为：

（6）

将内外螺纹的变形进行累计，可得：

（7）

2.3 螺纹副载荷分布规律

将螺母与螺栓沿啮合线展开，将得到一个直角梯形与一个长方形，水平面为直角梯形下底，斜线上为螺栓，螺纹啮合线与支承面存在一个角度为β的螺纹升角，啮合线所在的平面与水平面存在一个夹角α为螺纹牙型半角。

旋合螺纹的展开说明如图2所示。

图2 旋合螺纹展开说明图

根据图2旋合螺栓的展开图，可知螺栓杆受轴向载荷Q的作用。

将螺母左端设置为原点，在X处的轴向力为F，则位于z处的螺栓的伸长量εs和螺母的压缩量εb可由下式得出，即：

（8）

式中：As—螺栓横截面积；Ab—螺母横截面积；Es—螺栓材料弹性模量；Eb—螺母材料的弹性模量。

取Z=z，可得出εs,εb,δs,δb之间的关系为：

（εs+εb）z=z=（δs+δb）z=z-（δs+δb）z=0

（9）

把式（7～8）代入式（9），对z进行微分可得：

（10）

将式（10）转变，可得：

（11）

由螺母承载比例式（11）可得：

（1）Es/Eb、导程角β对螺母各螺纹牙载荷分布有所影响；

（2）由于螺距P与螺栓大径D决定了螺栓的导程角β，是影响螺纹承载分布的直接因素；

（3）梯形牙型螺纹各螺纹牙载荷均布性将优于三角形牙型螺纹。

在下文中，笔者用三维有限元分析法对此结论进行验证。

3 螺纹副载荷分布有限元分析计算

螺纹结构复杂，在进行三维有限元分析时，有较复杂的螺纹接触以及数量庞大的网格数量问题，一般在进行有限元分析时，常常使用无螺纹结构的简化模型，会导致分析结果出现误差。

为更准确地得到螺纹载荷例分布规律，笔者将使用ANSYS Workbench静力学模块对三维实体螺纹模型进行有限元分析。加入影响球控制模型网格数量，在螺母上施加旋转，当螺母旋转一定角度时，使螺栓拧紧，则可得到实体螺纹副载荷分布的规律。对比二维模型的有限元分析，其结果更加直观准确。

此外，ANSYS Workbench提供了强大的后处理功能，螺纹牙应力、螺纹牙的变形量、螺纹轴向载荷都可以由后处理或者计算得到。

笔者运用SolidWorks建模软件建立实体螺纹模型，通过ANSYS Workbench进行有限元分析。

3.1 实体建模

选取M8螺栓作为研究对象，笔者建立螺纹联接件三维模型，其中螺栓模型主要参数如表1所示。

表1 螺栓模型主要参数

3.2 有限元分析前处理

（1）导入模型。定义正确的单位，选取合适的坐标系，得到所需要的模型。

（2）定义材料属性。螺栓的材料为材料钢，材料参数如表2所示。

表2 材料参数表

（3）网格划分。为了简化模型，提高电脑运算速度，笔者对螺纹旋合处引入影响球控制，以提高螺纹副接触的网格精度；同时，减少整体模型的单元数量，通过影响球控制的三维有限元模型单元数量为163 915个，节点个数为53 273。

3.3 有限元分析求解

（1）边界条件的设定。螺纹副摩擦系数为0.15，在螺栓头部施加固定约束，夹件两端施加支撑约束；

（2）加载。将螺母轴向与轴向旋转的自由度约束打开，添加65°使其旋转，载荷施加时间为65 s;

（3）求解。采用Mechanical求解器进行求解。

3.4 结果后处理

螺纹连接范式等效应力分布如图3所示。

图3 螺纹连接范式等效应力分布图

由图3所示的螺纹连接范式等效应力分布图可以看出：螺纹的应力集中主要在旋合第一扣、螺栓头下圆角处、不完整螺纹处；最大等效应力与最大接触应力出现在旋合第一扣螺纹牙处；螺纹牙接触应力随着螺纹牙数增加，接触应力逐渐减小，符合螺纹副载荷分布特点。

笔者将螺母轴向按螺距等分成5个截面，计算各截面部分轴向力之比的分布。

螺纹截面应力如表3所示。

表3 螺纹截面应力

3.5 结果验证

笔者用SOPWITH 法和YAMAMOTO法对三维有限元分析结果的可靠性进行验证。

根据三维模型参数，可计算SOPWITH法螺栓轴向力的分布系数θ=23.55；YAMAMOTO法螺栓轴向力分布系数λ=0.42，取：x5=6.25，x4=5，x3=3.75，x2=2.5，x1=1.25计为螺纹牙i5，i4，i3，i2，i1可得旋合螺纹部分轴力之比的分布。

旋合螺纹部分轴向力之比分布如图4所示。

图4 旋合螺纹部分轴向力之比分布图

由图4所示的旋合螺纹部分轴向力之比分布图可知：三维有限元法分析得到的旋合螺纹部分轴向力之比与两种解析法有较高的拟合度，趋势相同；其中，第一扣系数最为接近。

根据三维模型的内外螺纹牙型参数，将其代入式（11），通过计算可得Ks=3.73，Kb=4.02，β=3.2；等效截面积As=0.23，Ab=0.22；螺纹啮合数N=5；并取点z1=22.36，z2=44.72，z3=67.08，z4=89.44，z5=111.8计为螺纹牙i1，i2，i3，i4，i5，可得各螺纹接触力与轴力比为：K1=35.7%，K2=15.17%，K3=10%，K4=7%，K5=5.6%。

可以看出：三维有限元法与螺母展开法得到的螺纹载荷分布趋势相同，尤其第一扣螺纹承载比最为吻合；通过螺母展开法，可得前三扣承载比例为60.87%，也符合现有的研究结论。

3.6 实验结果对比

笔者采用弹性韧性较好的PC+材料（弹性模量为2.32 GPa），通过3D打印建立实体螺栓；采用三角形牙型与梯形螺纹，螺杆大径14 mm,螺距2.5 mm，螺母螺纹牙数为5；施加1.1 N/m预紧扭矩。

笔者运用SolidWorks进行三维建模，通过3D打印得出的模型与三维模型尺寸在1∶1的比例下能很好地重合；对螺栓3D打印结构进行镶样，在5 mm处做切面；同时，对三维模型在同一螺纹面处做剖面；选取对应的螺纹剖面，调节三维模型截面的透明度与3D打印螺纹结构剖面重合，可得到螺纹牙变形图。

螺纹变形试验步骤如图5所示。

图5 螺纹变形试验步骤

对螺纹牙变形图进行图像处理，螺纹轴向平铺间隔为0.02 mm的直线，以螺纹旋合第一牙为例，可以得出第一螺纹牙轴向变形量δ1为0.08 mm。可得出螺母变形量为δ5=0.01 mm，δ4=0.02 mm，δ3=0.036 mm，δ2=0.046 mm，δ1=0.08 mm，得出螺纹变形试验得到各螺纹牙承载比例。

螺纹中面各螺纹牙承载比例如表4所示。

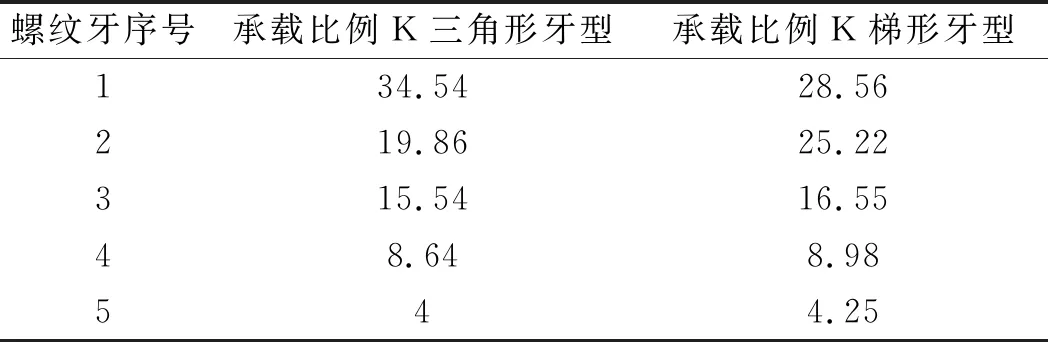
表4 螺纹变形试验得到各螺纹牙承载比例（%）

3种方法各螺纹牙载荷分布对比如图6所示。

图6 3种方法各螺纹牙载荷分布对比图

由图6所示的螺纹牙承载比例图可以看出：梯形螺纹牙承载分布优于三角形螺纹；第一个螺纹牙的承载的比例最大，并且随着螺纹牙序号的提高螺纹牙承载比例逐渐降低，并趋近于0。

螺纹变形试验法得出的数据与三维有限元法数据基本吻合，其结果与SOPWITH 法、YAMAMOTO法和螺母展开法理论分析法基本吻合，尤其第一扣螺纹承载比例最为吻合，因此可知，螺母展开法具有一定的可靠性，对重载螺纹联接件选型与设计有重要的作用。

螺纹变形试验模型制样优于光弹试验切片制备，通过3D打印螺栓模型精度较高，采用扭矩加载做镶样保证螺纹内部变形量的误差较小。由此可见，试验结果比光弹试验结果更加直观。

4 螺栓参数对螺纹副载荷分布的影响

将式（11）变形可得：

（12）

由式（12）可得到螺栓的参数牙型、导程角β、内外螺纹材料弹性模量比值Es/Eb等，以上参数都将影响螺纹牙载荷的分布。

采用三维有限元分析法，在加载不变的情况下，作出不同参数的分析，可得出螺栓参数对螺纹牙载荷分布的影响。

4.1 弹性模量对螺纹载荷分布的影响

笔者分别取Es/Eb为10，5，1，0.2，0.1，建立三维模型进行有限元分析，可得出不同弹性模量之比的螺母载荷分布，如图7所示。

图7 不同弹性模量之比的螺母载荷分布图

从图7可以看出：随着螺纹材料弹性模量之比增大，螺母承载比例曲线越来越平稳，所以当外螺纹材料的弹性模量大于内螺纹的弹性模量时，螺纹承载分布情况较为均匀。

4.2 螺距P对螺纹牙载荷分布的影响

d2一般由螺栓大径D确定，所以在螺纹参数中P/D确定了螺纹的导程角，笔者分别取1.25/8，1.3/8，1.4/8，1.5/8进行三维有限元分析，得出不同螺距的螺母载荷分布，如图8所示。

图8 不同螺距的螺母载荷分布图

由图8可以看出：在D确定的情况下，螺距P越大，螺母承载比例分布越不均匀；当螺栓大径D很大时，螺距P的变化对螺纹承载比例分布影响很小；螺栓大径越小，螺距P对螺纹承载比例分布影响就越大。

4.3 摩擦系数μs对螺纹牙载荷分布的影响

以M8螺栓为模型，笔者分别取μs=0.25，0.2，0.15，0.1，0.5进行有限元分析，得出不同摩擦系数的螺母载荷分布，如图9所示。

图9 不同摩擦系数的螺母载荷分布图

从图9可以看出：螺纹副的摩擦系数对螺纹载荷分布的影响并不显著，螺纹连接前3扣载荷分布改变并不大。由此可见，螺纹副的摩擦系数并不是影响螺纹载荷比例分布的关键参数。

4.4 牙型角对螺纹牙载荷分布的影响

笔者分别选择牙型角60°三角形螺纹与梯形螺纹的M8螺栓进行三维有限元分析，得出不同牙型的螺母载荷分布，如图10所示。

图10 不同牙型的螺母载荷分布图

从图10可以看出：梯形螺纹的载荷分布情况好于三角形螺纹载荷分布情况。

5 结束语

针对国内现有的螺纹设计没有系统的理论，为提高螺栓的可靠性与螺栓精确设计，本文采用螺纹展开法进行分析，推导出了沿螺纹啮合线方向的载荷比例公式，分别讨论了螺栓参数对螺纹承载比例的影响。结论如下：

（1）通过螺纹展开法得出了螺纹牙载荷分布规律，得出螺栓参数Es/Eb、P/D、牙型是影响承载分布的主要参数，并通过三维有限元分析法进行了系统的分析与验证；

（2）螺距P与螺纹弹性模量之比是影响螺纹载荷分布的主要参数；螺纹副摩擦系数μ对螺纹载荷分布影响较小；螺栓大径D很大时，螺距P的变化对螺纹承载比例分布影响越小，螺栓大径越小，螺距P对螺纹承载比例分布影响就越大；

（3）梯形螺纹的载荷分布情况优于三角形螺纹；

（4）外螺纹应选用弹性模量较大的材料，内螺纹应选用弹性模量较小的材料，这样可以相对减小螺纹载荷的分布不均。

基于ANSYS Workbench的三维有限元分析，本文得到了螺栓螺纹牙的应力分布规律，得出了各项螺纹参数对螺纹副载荷的分布规律，这对提高螺纹联接的可靠性有重要的意义。