基于改进基本尺度熵的轴承退化特征分析方法研究*

孙占民，唐旭明，万 浩，周银银，班东坡，闫 阁

（国网安徽省电力有限公司 淮南供电公司，安徽 淮南 232000）

0 引 言

卸船机、门机等设备是电厂码头重要的煤炭装卸设备，该设备的动力主要来自起升机构、行走机构以及俯仰机构，滚动轴承是上述三大机构中关键的旋转支撑部件。在港口恶劣的工作环境中，滚动轴承容易发生突发性故障，导致停工停产甚至伤亡事故。监测并采集滚动轴承的运行监测信号，在线准确评估健康状态，能够降低滚动轴承发生突发故障的概率，为实现基于状态的维修奠定方法基础[1]。基于状态的维修（CBM）主要包括退化特征提取、退化状态识别、剩余寿命预测等关键技术[2]。

退化特征提取的核心是定量表征机械设备的性能退化状态指数，是实现退化状态评估和故障预测的重要前提[3]，主要基于常用的时域、频域以及时频域分析等线性信号处理方法展开研究，例如峭度[4]、谱峭度[5]、自适应模态分解[6-7]等。考虑到负载的不规律变化以及机械振动信号的非线性、非平稳特性，近年来，基于信息熵与分形的复杂性分析方法开始应用到轴承、齿轮等旋转机械的退化规律分析中，包括近似熵、模糊熵、样本熵、盒维数、关联维数等特征[8-12]。

基本尺度熵以符号动力学理论为基础，对心跳间隔序列进行幅值上的符号化，并计算熵测度，具有较强的抗干扰能力，可以有效地分析短时、非平稳、有噪声干扰的数据。该算法起源并有效地应用在心脏电信号分析中[13-14]，在机械设备故障诊断领域也有一些初步应用[15-17]。但是目前对于机械设备特征分析的研究还相对较少。

本文对基本尺度熵算法进行改进，采用统一基本尺度对信号幅值进行符号化划分，定量衡量幅值变化的信息量；以IMS轴承试验中心的轴承全寿命数据为数据源，分析该方法在退化特征提取中的有效性。

1 基本尺度熵及其改进

1.1 基本尺度熵

一维信号的基本尺度熵计算思路如下：首先对数据进行从1维到m维的矢量转换，然后根据基本尺度参数a将m维矢量转换为相应的符号序列，最后由符号序列统计出相关概率，并计算基本尺度熵值[18]。

假设u为长度N的一维时间序列，首先将u转换成为m维矢量X，转换方式如下：

X（i）=[u（i）,u（i+L）,…,u（i+（m-1）L）]

（1）

式中：m—矢量维数；L—延迟因子，i+（m-1）L≤N。

当L=1时，u可以转化为N-m+1个m维矢量。之后，对每个m维矢量进行符号化，将其转换为m维矢量符号序列S，即：

Si（Xi）={s（i）,s（i+L）,…,s（i+（m-1）L）}

（2）

式中：s—符号类型，s∈A∶A=0,1,2,3。

转换过程如下：

（3）

式中：BS（i）—向量基本尺度。

其中，BS（i）表达式为：

（4）

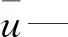
其中，a在实际应用中需要合适地选择。取值过大会丢失信号中的细节信息，无法反映信号的动态变化信息，取值过小则会受噪声影响。

最后，统计m维矢量符号序列S的分布概率P（Si）。由于包括4种符号，m维矢量符号序列共有4m种不同组合状态π。

因此，整个N-m+1个m维矢量中所占的概率为：

（5）

式中：t—符号向量序号，1≤t≤N-m+1；#—包含的个数。

序列u的归一化的基本尺度熵计算如下：

（6）

其中，m的取值可以为3～7，N的取值只要大于4m即可。

对所有可能的π的分布概率求信息熵，该信息熵描述了时间序列中m个连续值所包含的波动信息，即信息的复杂度。基本尺度熵的值越大，则表明序列维矢量的波动模式越复杂，序列的复杂性越高；反之，熵值越小，序列的复杂性越低[19]。

1.2 改进的基本尺度熵

基本尺度熵以作为符号划分标准，定量度量每个矢量距离基本尺度BS的波动模式，取值与波动模式的复杂性成正比。但该方法对每个矢量均需计算基本尺度BS，计算速度较慢，且参数a的取值会影响算法结果，不利于数据的在线分析。

以基本尺度熵方法为基础，基于符号动力学理论，笔者提出一种改进的基本尺度熵（improved basic scale entropy, IBSE）计算方法，其计算方式如下：

Step1：将一维时间序列u转换成为m维矢量X。

X（i）=[u（i）,u（i+L）,…,u（i+（m-1）L）]

（7）

Step2：采用网格化方法对每个m维矢量进行符号化，转换为m维矢量符号序列S，即：

Si（Xi）={s（i）,s（i+L）,…,s（i+（m-1）L）}

（8）

式中：s—符号类型，s∈A∶A=1,2,3,4,5。

转换方式如下：

（9）

式中：BS0—统一的基本尺度。

本文采用正常状态振动信号的均方根。改进的基本尺度熵方法采用统一的符号划分标准，能够定量度量信号幅值分布的模式；同时，由于采用统一的尺度，算法速度较快。

最后，在式（9）的符号化模式下，绝对值小于基本尺度的信号会被符号化为同一种符号，降低了算法对于噪声的“敏感性”，在一定程度上提升了算法的抗噪能力。

2 IMS轴承全寿命数据分析

2.1 滚动轴承全寿命实验

笔者采用来自辛辛那提大学智能维护系统中心（intelligent maintenance systems，IMS）[20]的滚动轴承全寿命数据集进行实例分析。

加速寿命实验台示意图如图1所示。

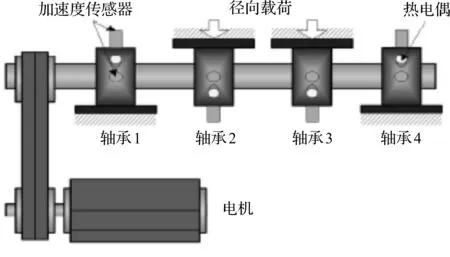
图1 加速试验台示意图

图1中，轴上安装了4套Rexnord ZA-2115双列圆柱滚子轴承，每列含16个滚子，滚子组节圆直径为75.501 mm，滚动体直径为8.407 4 mm，压力角为15.17°；轴转速保持2 000 r/min恒定不变，通过弹簧装置在轴上加载2 721.554 kg径向载荷；每个轴承座安装2个高灵敏度PCB加速度传感器353B33采集振动数据；采样频率20 kHz，每组采样时间为1 s，组间采样间隔为10 min。

该试验台的4套轴承从2019年2月12日11:16:18运行至2月19日06:22:39，共采集到982组文件数据。试验台停机时，检查发现：1#轴承出现故障，失效形式为外圈故障[21]；其余2#～4#轴承完好。

2.2 参数影响分析

笔者依次对每组信号进行符号化，并提取改进的基本尺度熵参数。在计算过程中，基本尺度BS0和矢量维数m是IBSE计算过程中的两个主要参数。

笔者以第750组数据为例，分析参数对IBSE数值的影响。

基本尺度BS0的影响规律如图2所示。

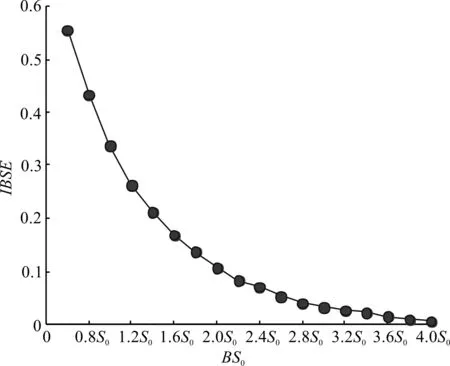
图2 基本尺度BS0影响规律

由图2可以看出：基本尺度BS0与IBSE的取值成反比；基本尺度越大，取值越低。其主要原因在于基本尺度直接决定符号化的基准值，取值越高，符号化的模式数量越少，熵值越小。

为了保持较高的特征值分辨率，本文选取BS0为1.5倍的正常运行信号的均方根（S0）。

m取值对IBSE的影响如图3所示。

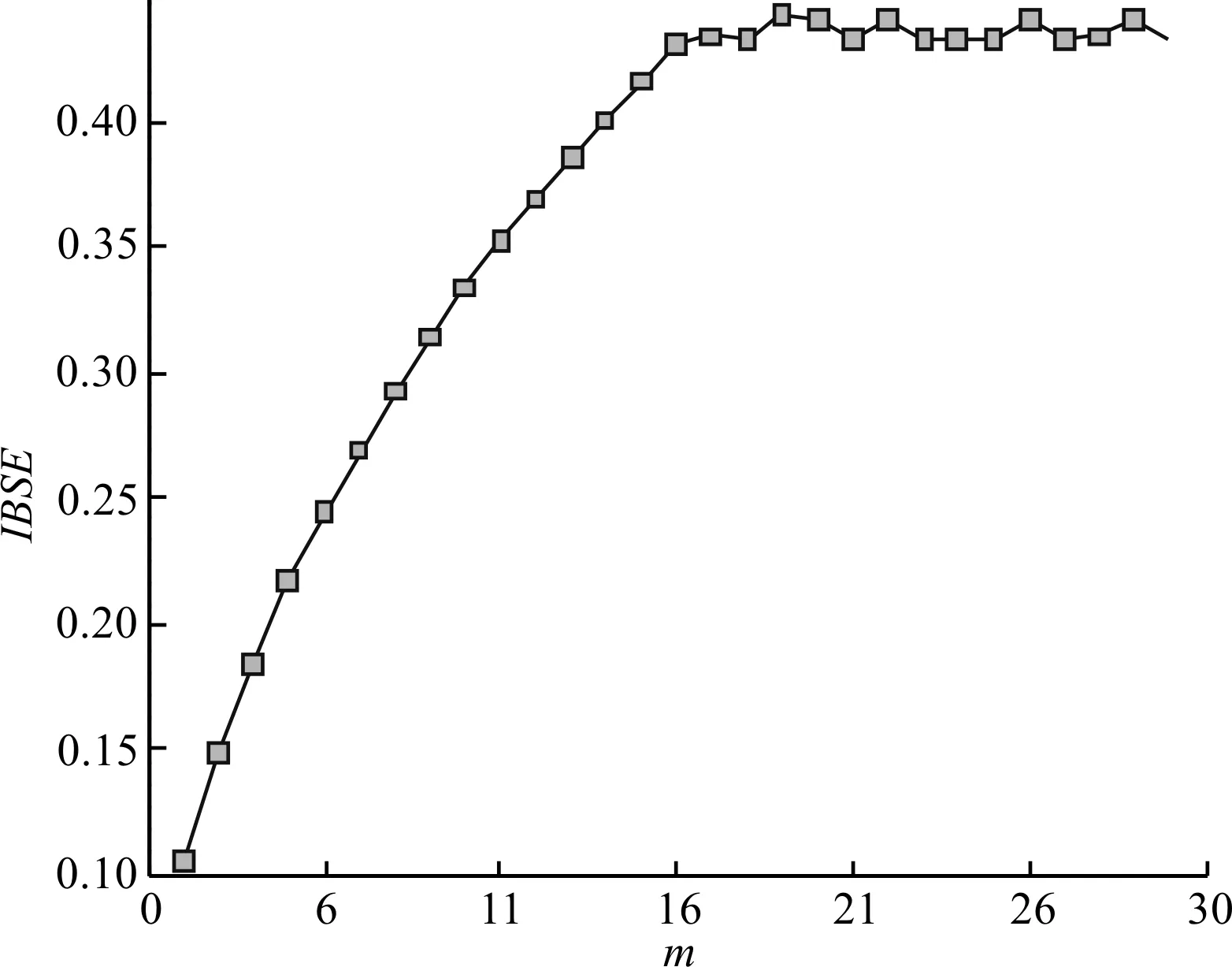
图3 m取值对IBSE的影响

由图3可以看出：m取值越大，IBSE取值越高，与原算法是一致的；当m>16时，IBSE趋于稳定。

考虑到算法的计算量和运算速度，本文选取m=4。

2.3 基本尺度熵退化特征提取

笔者分别计算每组数据的IBSE。

IBSE变化曲线如图4所示。

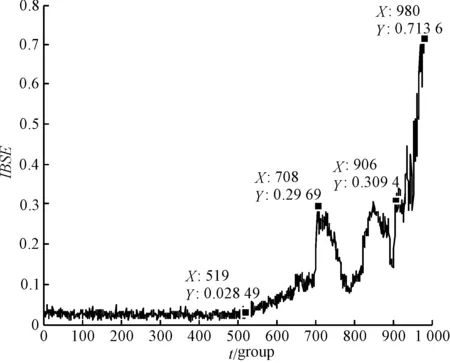
图4 IBSE变化曲线

由图4可以看出：随着性能退化程度的加深，IBSE取值整体增加；曲线呈现明显的阶段性，且信号波动性低。

按照基本尺度熵方法，笔者分别计算每组信号的BSE参数。

BSE变化曲线如图5所示。

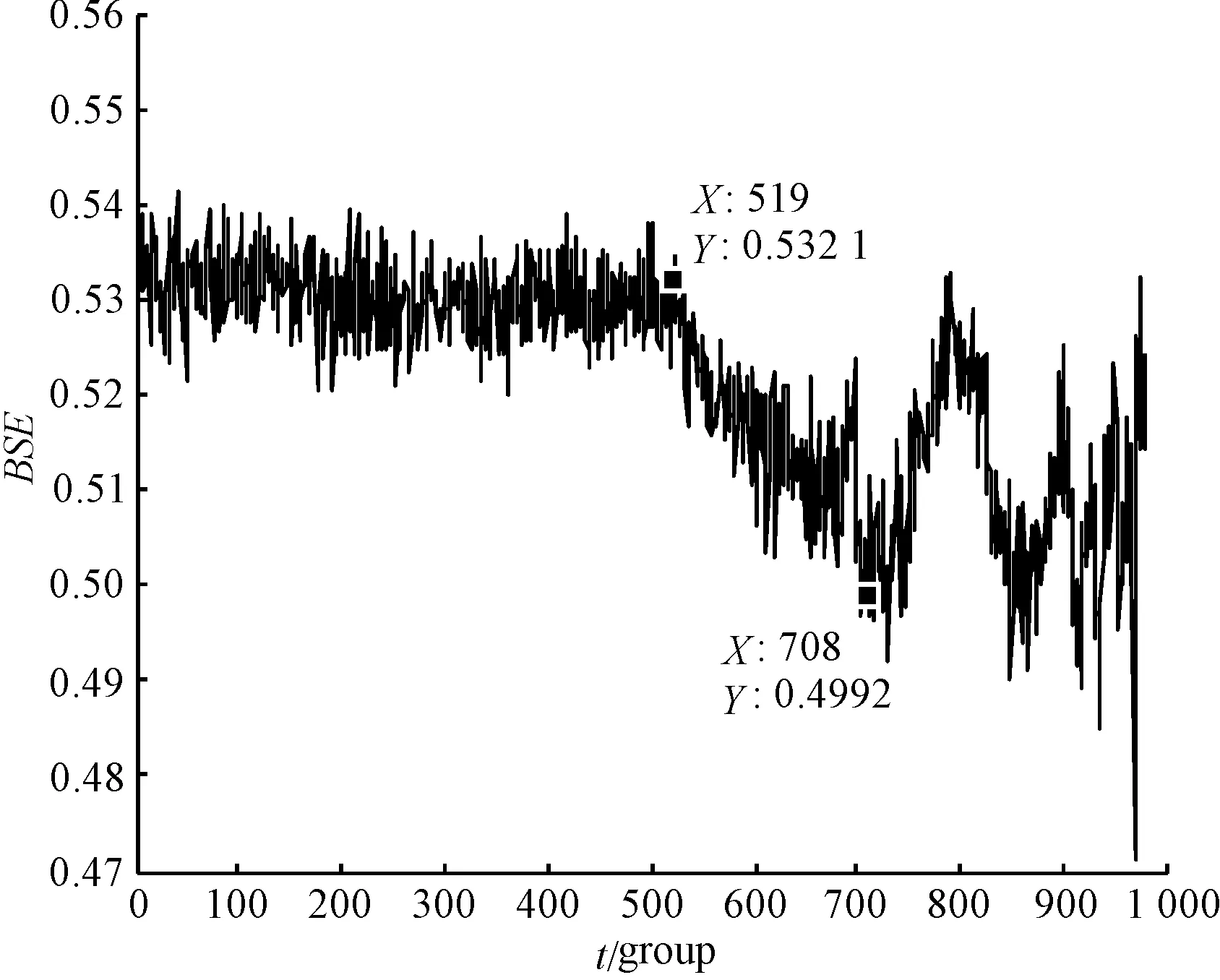
图5 BSE变化曲线

对比图（4～5）可以看出：随着性能退化程度的加深，BSE取值整体减小。其主要原因在于BSE算法衡量每组数据的波动模式，正常状态下分布均衡，取值最高，随退化进程而降低；IBSE采用统一的尺度衡量幅值分布信息，性能退化程度越深，分布模式越均衡，IBSE取值越高。

同时，由于对幅值区间的符号化，使该算法能够过滤噪声引起的干扰，使曲线波动更小，稳定性更强。

2.4 基于改进基本尺度熵分析方法的优势

笔者选取常用的复杂度指标（近似熵、模糊熵、样本熵）以及有效值进行对比。

不同退化特征对比如图6所示。

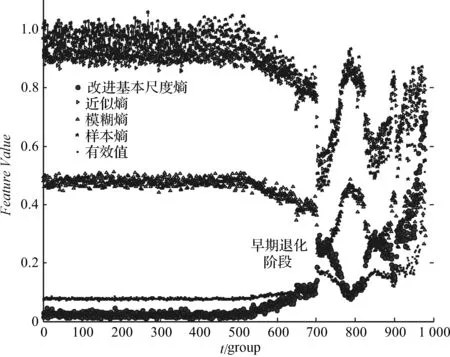
图6 不同退化特征对比示意图

由图6可以看出：复杂度指标的取值与退化程度成反比，退化程度越深，取值越低；改进的基本尺度熵与有效值指标分别反映了幅值分布和能量累积，取值与退化程度成正比，退化程度越深，取值越高；在第500组数据时，滚动轴承出现轻微退化，此时近似熵、样本熵、模糊熵以及改进基本尺度熵均发生了敏感的变化，而有效值参数由于只能反映时域的统计特性，未能敏感地表现出该趋势。

不同算法的定量结果对比如表1所示。

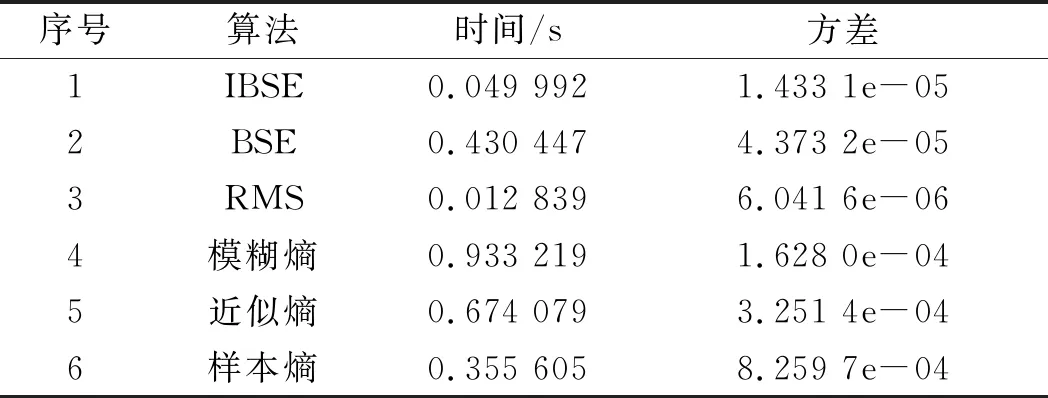
表1 不同算法定量结果

表1描述了算法对每组数据的平均计算时间，以及曲线稳定区间[0,500]的方差大小。

由表1可以看出：改进基本尺度熵运算速度快于基本尺度熵以及其他复杂度指标，其主要原因在于计算过程中统一的符号化运算；而在曲线的稳定性方面，改进的基本尺度熵也要优于复杂度计算方法；有效值RMS具有最优的运算速度和方差，但对于轴承性能的轻微退化不敏感。

3 结束语

针对基本尺度熵方法存在稳定性不强、误差较大、计算速度慢的不足，本文提出了一种改进的基本尺度熵方法，并将该方法应用到滚动轴承的退化特征提取中，并以IMS轴承全寿命数据进行了算法验证，结果表明：

（1）改进的基本尺度熵能够有效描述序列的模式变动的复杂度大小。信号稳定性越强，模式变动越简单，取值越低；反之，模式变动越复杂，取值越大；

（2）通过引入统一的基本尺度，算法对于噪声的敏感性降低，计算速度加快，能够有效挖掘信号符号模式的变动趋势；

（3）当滚动轴承的健康状态逐渐退化时，信号的改进基本尺度熵取值逐渐增大，能够在一定程度上跟踪性能退化的进程，并且能够清晰地反映性能的初步退化，为进一步作在线退化特征提取奠定了基础。