基于二维截面筛选标记的点云简化方法研究*

刘菲菲，杨 铎

（大连大学 机械工程学院，辽宁 大连 116622）

0 引 言

近年来，非接触式测量方法因为其方便简单的操作，在逆向工程领域中多有应用，尤其是在复杂曲面零件的逆向数字化扫描。

随着电子计算能力的提高和扫描设备的高精度化，更高数量级点云在非接触测量方法中出现，也带来了大量噪声和冗余数据点。为保证后续逆向工作能够高效完成，必须做好点云的预处理。一般包括点云去噪和点云简化两步，先用滤波法去除有序或部分有序的大尺度噪声干扰。

吴玉泉等[1]用空间单元格对点云进行了点云空间的有序划分，得到了各个单元格内的“中心点”，并求出了距离标准偏差，根据设定的相应阈值进行了去噪。Rosman G[2]在标准基础模型和距离扫描上应用补丁协同谱分析，其鲁棒性较高，应对无序点云的去噪效果较差。崔鑫等人[3]提出了基于特征信息的加权模糊C均值聚类去噪算法，保持了点云本来特征，适用范围较广，从图形上看模型线条略尖锐。史皓良[4]提出了基于点云曲率特征信息分类去噪法，针对两种不同特征区域分别去噪，即邻域距离平均滤波和自适应双边滤波，突出了点云主体，在特征丰富区域（角点和相交的边界线上）有较大偏差；文献[5]同样是对不同尺度的噪声进行了分步处理，结合了点云模糊均值聚类和点云双边滤波去噪的方法，去噪效果较佳。

由于小尺度噪声往往不具有明显规律，对其的处理放在点云精简过程中。精简的目的则是去除点云主体中的重复点和冗余点，用最少的点表示最多的信息。Shuai Yuan等人[6]认为传统算法经常丢失几何信息并且没有动态扩展结构，提出了一种基于共形几何代数的简化算法：利用球形树构造了多分辨率细分，利用k均值聚类计算了最小边界球，然后用两种具有远程计算便利性的简化方法进行了自我分割，适应性简化。

近年来出现一种代替简化法[7-8]：先基于距离的聚类算法对点云进行分类，在估计曲率较小的簇里可以用簇中心代替簇中所有点从而简化点云。

本研究提出一种与传统处理方式不同的点云简化算法—二维截面筛选标记法。

1 算法设计

1.1 预处理流程

点云的预处理流程如图1所示。

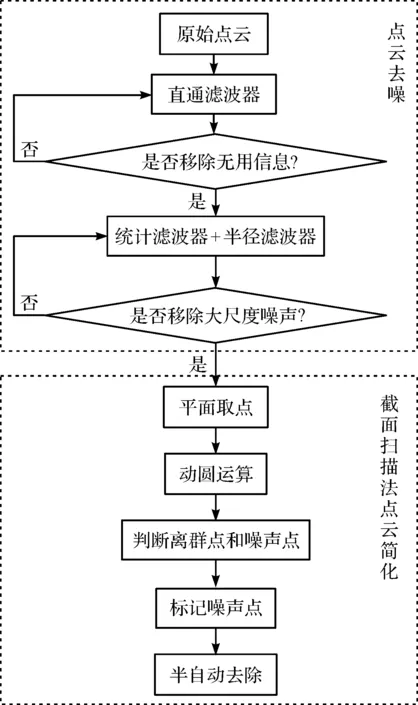
图1 预处理流程

图1中，直通滤波和统计滤波根据文献[9]设置。

1.2 截面扫描法

1.2.1 坐标系转换和选定截面

点云数据最初坐标系为局部坐标系LCS，点云坐标点用（xl,yl,zl,R,G,B）表示。用一长方形截面截取点云数据，截面所在面作为新建物体坐标系MCS中的XOY面，截面一角作为新坐标系下的原点O，其它角点坐标分别为（a，0）、（0，b）、（a，b），截面面积为ab，点云群方向为正Z轴。

在截面上点的坐标（xl,yl）根据旋转和平移原则转化为新坐标（xm,ym），Zl坐标不做改动。

截面选取如图2所示。

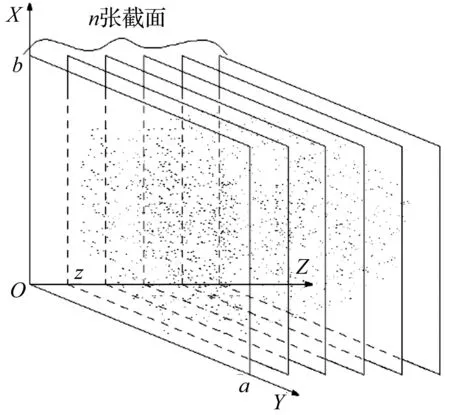
图2 截面选取

选取的截面向Z轴正方向每次移动z距离作为新截面，z为点之间最小平均间隔，共移动n次，共n+1张截面。n和由点云在Z方向总长度确定，使全部点云密集区被截面所截取；z由点云密度确定。为节省运算空间，点不超过5个的截面忽略不计算。每一截面转化为新坐标系，其点随之转换为新坐标。设置点云截面面积大小固定，保证每一片都能将点云主体包括在内。若点云主体有需要剔除缝隙杂点的部分，在截面选取时，取能使缝隙在截面上投影面积最大的面。

1.2.2 选定扫描域

本研究在截面上取一圆形扫描域，圆心为原点坐标（xo,yo），根据计算的平均点间距[10]取圆的半径为r（小于密集区点云平均距离），此时在直角坐标系下圆的方程为x2+y2=r2，扫描域按照设定方向运动，圆心为（xa,yb）圆的方程变为：

（x-xa）2+（y-yb）2=r2

（1）

扫描域初始运动方向如图3所示。

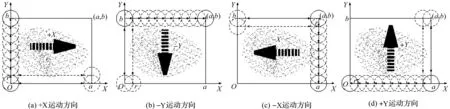
图3 扫描域初始运动方向

4个主运动方向+X，-Y，-X，+Y分别在图2中用箭头标注。以图3（a）的+X方向为例，圆的圆心从（0，0）直线运动到（a，0），触到对边返回或按2.2中介绍的触点返回（0，0）点，在Y轴方向运动r距离，圆心到点（0，r），再继续沿+X方向运动触边或触点返回，至此以往到达（0，b），进入主方向-Y运动。-Y，-X，+Y方向的运动规律同理。

1.2.3 筛选和标记

目标是筛选密集区外的孤立点和密集区轮廓的边沿非模型点，将孤立点记为A点群，能显示轮廓的点记为B点群，白色或浅白色点即颜色坐标（R，G，B）>（250，250，250）的点标记为C点群，仅有B标记的点组成的点云即为实际轮廓组成的主要部分。

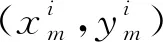
第一次触点，I=1，此时圆心坐标为（xa1,yb1）：

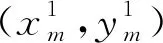
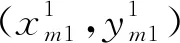
（3）N>2，N个点的排序方式同理，因为圆初始沿直线方向运动，遇到的点必然在圆的下半弧段，取使连成的弧段最长的两个点，两点中点与圆心连成的射线方向为扫描域的新运动方向。

扫描域改变运动方向进行第二次触点，I=2，有以下a、b两种情况：

（a）当第1次触到的某点再次落在圆上，即将运动到圆外时，若圆上仍未出现新点，则将第1次触的N个点标记为A+x，且扫描域弹回初始路径中的截面边继续运动，运算下一条直线运动的触点过程；

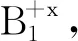
有向面积法用到向量积，顺序输入多边形每个顶点的坐标，按同样的顺序（顺时针或反时针）两两叉乘。多边形面积即为向量积之和的绝对值的一半。

设多边形由点P0，P1，…，PN-1连线围成，则面积S为：

（2）

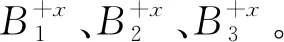
为降低循环次数，设置最多可触点ε（1≤ε）次，期间若S始终小于S0，扫描域不继续运动，返回截面边。到下一条直线上的运动规律相同，但屏蔽截面上有标记的点，不再被圆识别，避免重复标记。扫描域从坐标原点到达截面下一角，在大方向-Y的每一条直线中继续筛选A和B点群，当4个大方向的点群筛选完毕后，这一截面上的密集区外孤立点和轮廓均点已清晰标记。

向Z轴正方向移动z距离的新截面再次进行筛选，当n+1张截面筛选完毕后，开始点的自动剔除和手动剔除工作。

1.2.4 半自动剔除

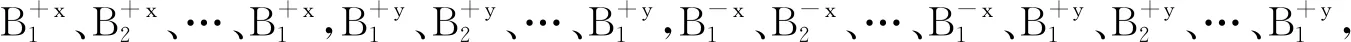
2 仿真实验

2.1 实验设置

为利用单目视觉技术恢复典型机械零件夹头的点云三维模型，笔者初步重建得到点云数目为625 482。点云可分为高密度点云和低密度点云。由文献[11]知，点云数量在一万以内为低密度点云，如CMM测量所得；几万至几千万的点数为高密度点云，通常由光学测量法所得。本研究使用图像扫描法三维重建设备，生成数十万点数的中高密度点云。

其中，a方向和b方向的点云模型如图4所示。

图4 a方向和b方向的点云模型

零件a方向长度为50 mm，尺寸为0.2×0.2×0.2 m3。实验装置有柔光棚、转台、单反相机（佳能500D）。对夹头拍摄144张图片，按单目视觉原理合成零件表面轮廓的点云模型，在VC++平台上结合OpenGL实现算法流程，通过处理点云数据包含零件位置、点的位置和颜色等信息，对模型进行滤波去噪和简化。

2.2 实验结果与分析

由塔型分解算法[12]计算得点云分辨率为3 μm/mm，可直接标记出C点有6 379个。为将零件的中间空洞部分筛选出更多孤立点，截面从图3（a）中a方向从左至右运动，在物体坐标系中Z方向最长52 mm，由此计算。

根据大量实验发现有3种因素最为影响筛选点数：截面面数n、扫描域半径r（μm）、触点次数I。为清晰显示轮廓，笔者为每个因素选取5种水平，做L25（35）正交实验，得出B标记出的孤立点数只和面数有关，因为面数越多，筛选得到的总体点数相应增加，运算时间也会增多，但较另外两因素的对标记点数量影响较小。

固定截面面数为16 000，通过对另两个影响因素试验得到检测出的轮廓点数量随触点次数变化规律如图5所示。

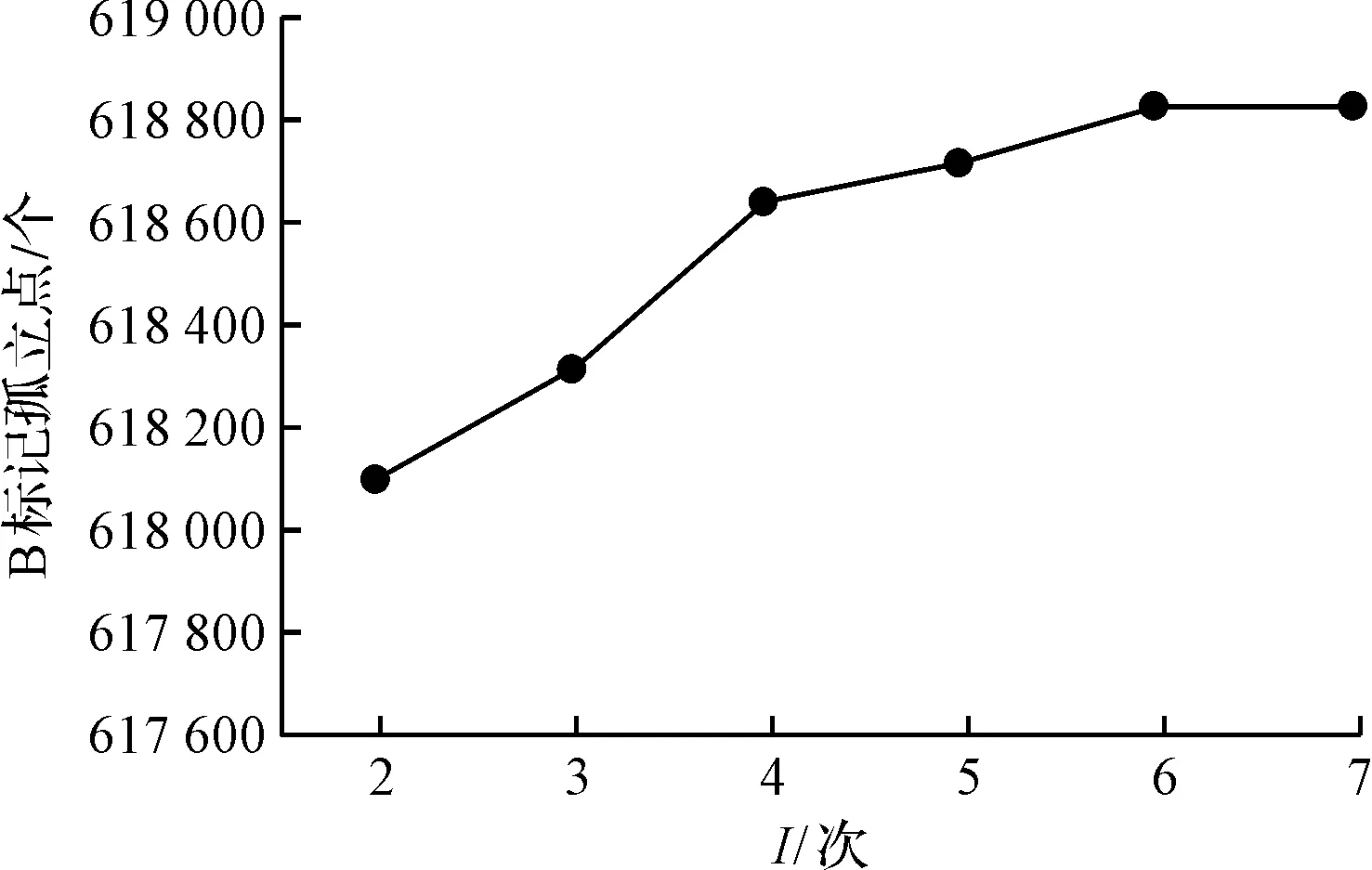
图5 检测出的轮廓点数量随触点次数变化规律

由图5可知，B标记的孤立点数随I增大而增大，到一定程度检测出的点数趋于稳定，但检测时间和检测误差也相应增加。综合运算时间和标记点数量等因素，得最佳触点次数为4。

固定I为4，扫描域半径分别为2.3 μm,2.5 μm,2.7 μm,2.9 μm进行简化，检测出的轮廓点数量随触点次数变化的局部简化效果如图6所示。

图6 局部简化效果图

图6中，随触点次数增加，检测出的轮廓点数量增加，但发现其中点云模型丢失一部分关键特征，所以取扫描域半径2.7 μm为最佳参数，约分辨率的0.93倍。

文献[13]采用连续变形简化算法来简化点云。为验证本文算法的有效性，笔者在Intel Core i7-6700K CPU、运行内存32GB、Windows10 64操作系统环境，于VC++平台上结合OpenGL实现本文简化算法中自动去除模式，处理夹头点云模型。

同操作环境下，用连续变形法处理夹头点云数据。笔者用两种方法分别进行点云预处理的局部效果，如图7所示。

图7 两种方法分别进行点云预处理局部效果图

由图7可知，夹头夹缝内处理情况较优的是本研究方法。

处理过程记录了运行时间并计算相关参数，笔者列成本文算法和连续变形法的客观性能对比，如表1所示。

表1 本文算法和连续变形法的客观性能对比

表1中，Emax、Eave分别为点云模型光顺的最大顶点误差和平均误差，Emax越小说明点云质量越好；Eave反映模型整体的噪声情况，其值越小，说明算法鲁棒性越强。从表1中得出：本文算法平均Emax和Eave均低于连续变形法，在运算时间上也有优势。

3 结束语

本研究介绍了截面筛选标记的点云简化算法，提出了点云数据降维处理思想，强调在截面上要进行统一坐标变换，需要根据点的密集程度选取截面数量；在二维平面内处理点的位置坐标和颜色等信息。点云滤波去噪和截面筛选标记简化相结合的方法鲁棒性较好，总体运行速度满足普遍需求，可以充分去除小尺度噪声点和冗余点。实验结果表明：

（1）本研究算法适应性强，与大尺度去噪的直通滤波、统计滤波及半径滤波结合使用，可以处理同时具有多种噪声的中高密度散乱数据点集；

（2）算法在去除噪声的同时，良好反映物体三维特征，防止模型的过光顺。

与连续变形法比较，本研究方法的三维点云数据模型整体预处理情况较好，光顺误差小。由于扫描域半径和扫描次数等阈值的选择需要根据点云分辨率以及实际经验来确定，如何自适应的选择最优参数是本研究方法今后研究的核心。