不同制造子行业研发投入对盈利能力影响的差异研究

吉轩帆 梅姝娥

(东南大学经济管理学院，南京 210096)

技术创新既是企业赢得竞争力的关键，也是国家和区域经济持续高质量发展的关键，而技术创新一方面需要大量的资源投入，另一方面存在收益不确定性、投入回收时间长等特性。近年来我国研发投入快速增长，特别是制造业研发投入快速增长。为此，剖析我国制造业企业研发投入对企业绩效的影响方式，充分发挥有限研发投入的作用具有重要意义。

国内已有大量文献从不同角度探讨了我国企业研发投入与绩效的关系。张永安等以信息技术产业上市公司为研究对象，发现研发投入与当期主营业务收入正相关[1]；孙维峰等以沪深两市制造业上市公司为样本，认为研发强度与销售回报率正相关[2]。马艳艳等则认为，研发支出与总资产回报率存在“U形”关系[3]；戴小勇等研究发现，研发投入存在门槛效应[4]。任海云等认为制造业企业研发投入与未来1～3年的主营业务利润率正相关，且相关系数呈逐年递减趋势[5]；陆玉梅等发现，制造业和信息技术业上市公司的研发投入虽然与当期企业绩效负相关，但与未来1～2年的绩效正相关，且在次年的影响更大[6]。

目前研究文献大多针对某一类企业、讨论某一个方面的影响，少有文献讨论制造业不同子行业间研发投入与盈利能力关系的差异性。而不同子行业的技术创新有着不同的特点，研发投入的作用机制存在差异。为此，本文研究制造业不同子行业研发投入与其盈利能力间关系的差异性。

1 研究假设

1.1 研发投入与企业盈利能力的关系

一方面，研发投入对盈利能力具有正面影响。Wang等认为研发主要通过减少生产成本和发布新产品来提升企业盈利水平[7]。Bowen等认为创新会使企业产生新的有价值的、稀缺且难以模仿的资源，形成竞争优势并获得经济租金[8]。

另一方面，过量的研发投入也可能对企业盈利能力产生负面影响。研发投资是一种要素投入，必然会服从要素的边际报酬递减规律。一旦投入超过某一阈值，增加的研发费用并不能产生相应的回报。Chen等认为，由于研发的潜在收益无法得到保证，过量的研发投资存在昂贵的机会成本[9]。此外，戴小勇等也指出，研发投资不可过低，否则企业可能无法获得应有的创新效果；即使有所创新，也可能被竞争对手模仿，无法带来竞争优势[4]。由此提出假设：

H1：对于制造业企业，研发投入与盈利能力存在非线性关系。

1.2 研发投入对盈利能力影响的滞后性

一方面，企业从研发投资到产生绩效需经过一定时间的转化，从最初立项到形成新的知识或技术，再应用到产品获利需要一定时间。

另一方面，研发投资对绩效的影响可能会延续多期。有学者认为，制造业企业将研发投资转化为新产品或新技术，当市场中其他企业未掌握这些技术时，研发就会给企业带来竞争优势。但当竞争对手也掌握类似技术或生产相似产品后，该竞争优势便不复存在，因此影响期限的长度是有限的。据此提出假设：

H2：制造业企业研发投入对盈利能力的影响存在滞后性。

1.3 不同制造业子行业间研发与绩效关系的差异

不同行业，不同产品的技术存在很大差别，García-Manjón等指出，研发投资与企业销售增长之间的关系取决于不同的行业和国家[10]。Yeh等也提出，由于行业成熟度的不同及产品生命周期的差异，研发的时间跨度可能有很大不同[11]。据此提出假设：

H3：对于不同制造业子行业，研发投入与企业盈利能力的关系存在差异。

2 研究设计

2.1 模型选择

由于本文假设在不同研发投入范围内，其与盈利能力的关系存在差异，为避免人为划分研发投入区间产生的误差，本文采用Hansen所提出的面板门槛回归模型。该模型能根据数据本身的特征来划分区间。

该模型要求样本为存在个体固定效应的静态平衡面板数据。单门槛的面板回归模型如式(1)所示：

(1)

其中，yit是被解释变量，本文为企业盈利能力指标；xit为解释变量，qit为门槛变量，本文为研发投入指标；γ为待估门槛值；I(·)为示性函数；μi为衡量个体异质性的截距项；eit为随机误差项。

Hansen采用“格点搜索法”，将使残差平方和最小的门槛值γ＾作为门槛变量的估计值。由于检验门槛效应是否显著的F统计量不服从标准分布，Hansen通过Bootstrap法获取其渐进分布及相应的P值。接着构造似然比统计量LR来检验估计值γ＾是否等于真值γ。双门槛面板回归模型的表达式如式(2)所示：

(2)

其中，门槛变量γ1<γ2。对于参数估计，首先确定单门槛模型的估计值γ＾1，在此基础上再利用“格点搜索法”，寻找使残差平方和最小的第二门槛值γ＾2，再固定γ＾2反过来修正γ＾1，此时的估计值渐进有效。最后对双门槛效应是否存在及门槛估计值是否等于真值进行显著性检验。类似的方法可扩展到多门槛回归模型中。

2.2 变量选择

被解释变量，本文重点讨论企业研发对盈利能力的影响。衡量企业盈利能力的指标非常多，因此本文选用主营业务利润率。

解释变量和门槛变量。为使不同规模企业的研发投入程度具有可比性，选用研发强度作为解释变量，具体用研发投入占主营业务收入的比重。本文研究不同研发强度下，研发投入与盈利能力间的关系，因此门槛变量也选择研发强度。

控制变量。为了较全面分析不同企业研发投入对绩效的影响，本文选择资本结构、企业规模、企业年限、营销强度和所有权结构等作为控制变量；参考相关文献，选用资产负债率作为资本结构的衡量指标，企业年末总资产的自然对数衡量企业规模，销售费用占营业收入的比重来衡量营销强度，用前2～5大股东持股比例占第一大股东持股比例的比重衡量所有权结构。模型变量的符号及取值方式如表1所示。

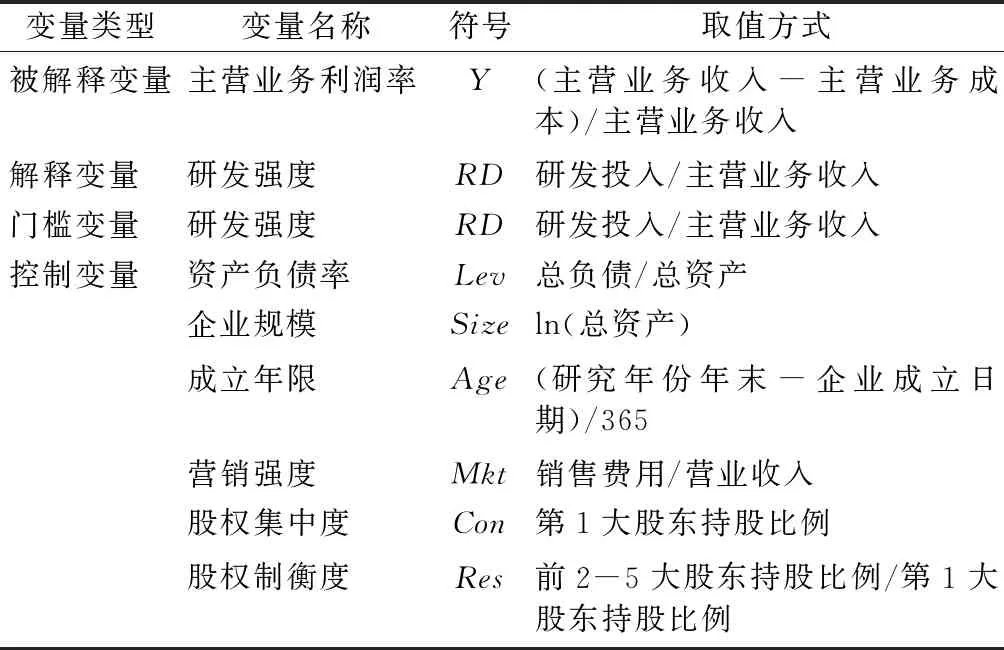
表1 模型变量的选择和取值

2.3 数据收集与处理

本文选择2013—2018年沪深两市A股上市的制造业企业数据。剔除此期间内被标为ST及未披露研发信息的企业，还剔除期间所属子行业发生变动的企业。同时，为使结论更具稳健性，研究剔除样本数不足100的子行业，最终保留以下5个子行业：26-化学原料及化学制品制造业、27-医药制造业、34-设备制造业(包括通用设备和专用设备)、38-电气机械及器材制造业、39-计算机、通信和其他电子设备制造业，样本数分别为：115、126、176、132、177。所有数据均来自CSMAR数据库及上市公司年报。

为减小极端值的影响，本文借鉴了李显君等的处理方式，对研发强度和主营业务利润率进行Winsorize处理，将1%以下和99%以上的数据分别用1%和99%的数值替换。

3 实证结果与分析

3.1 描述性统计

5个制造业子行业中样本企业的主营业务利润率和研发强度的描述性统计结果如表2所示。不同行业的研发强度和主营业务利润率均存在显明差异，不同行业内部企业间的差异也明显不同。

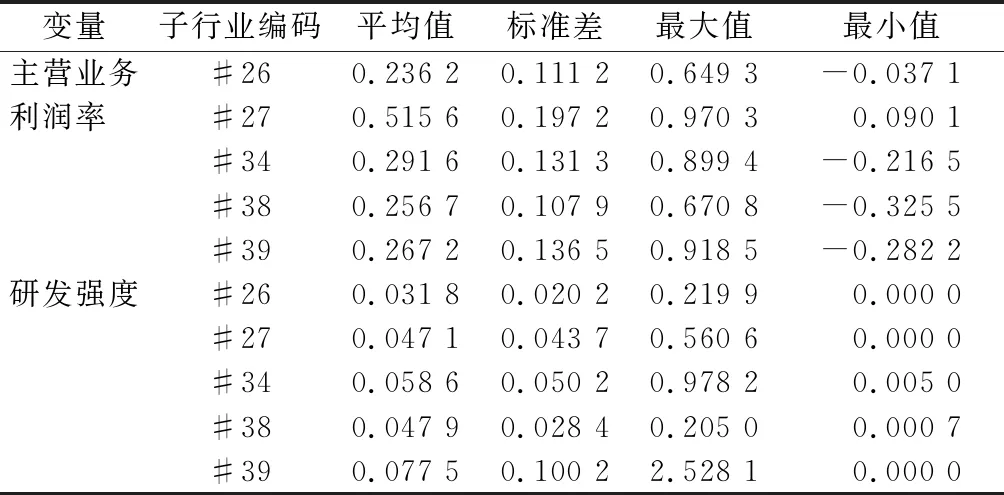
表2 关键变量的描述性统计

3.2 相关性分析

对模型变量的Pearson相关性检验结果如表3所示，结果表明，样本中制造业企业的研发强度与主营业务利润率在1%显著性水平下正相关。计算5个制造业子行业中解释变量和控制变量的方差膨胀因子VIF，结果如表4所示，各变量的VIF都小于10，说明模型不存在多重共线性问题。

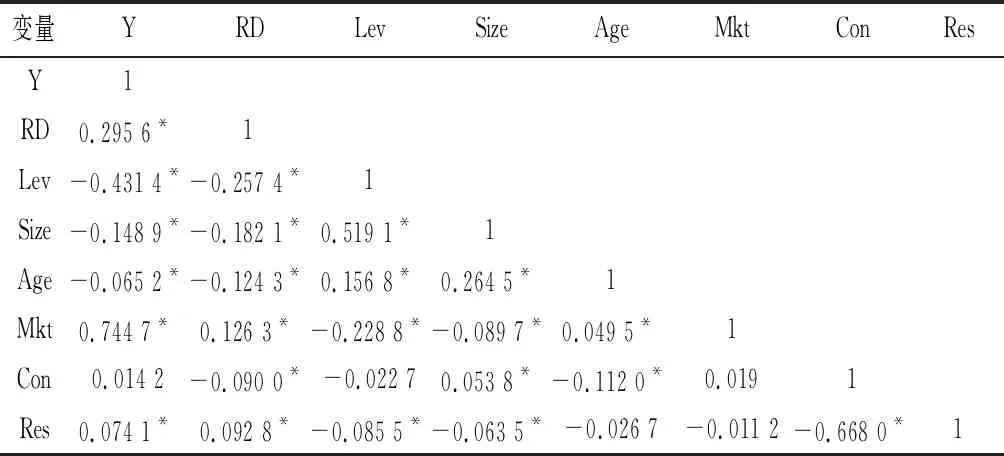
表3 变量的Pearson相关性检验

注：表中*表示在1%显著性水平下显著

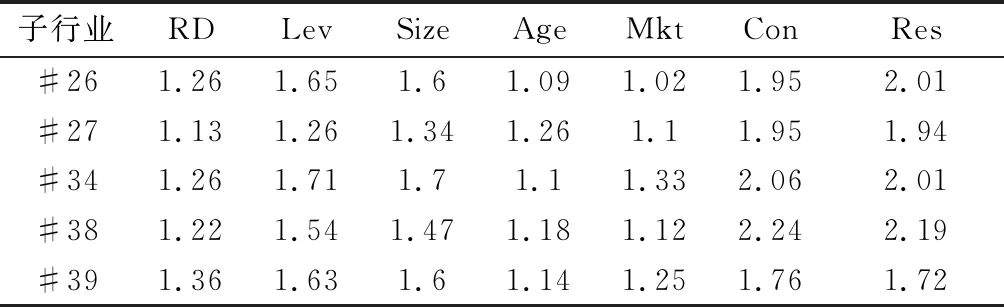
表4 解释变量和控制变量相应的方差膨胀因子(VIF)

3.3 门槛回归分析

Hansen的面板门槛回归模型要求样本为存在个体固定效应的面板数据，经过相关检验和分析，本文数据符合要求。

3.3.1 门槛效应检验

分别对5个制造业子行业的样本数据进行单门槛、双门槛、三门槛的显著性检验。同时，考虑研发投入对盈利能力影响可能的滞后效应，同时检验了当前期、滞后一期和滞后二期研发强度对主营业务利润率的影响。表5列出用Bootstrap法计算出的F统计量和相应的P值。若P值小于5%，则认为存在门槛效应。为保证结果的稳定性，研究将Bootstrap的次数设为500。

由表5可知，在5%显著性水平下，医药制造业当期及滞后一期存在显著的单门槛效应；设备制造业存在滞后一期单门槛效应；电气机械制造业存在当期及滞后二期单门槛效应； 计算机、通信和其他电子设备制造业存在当期双门槛效应及滞后一期单门槛效应；在化学原料及化学制品制造业未检测出显著的门槛效应。门槛估计值及95%置信区间如表6所示。

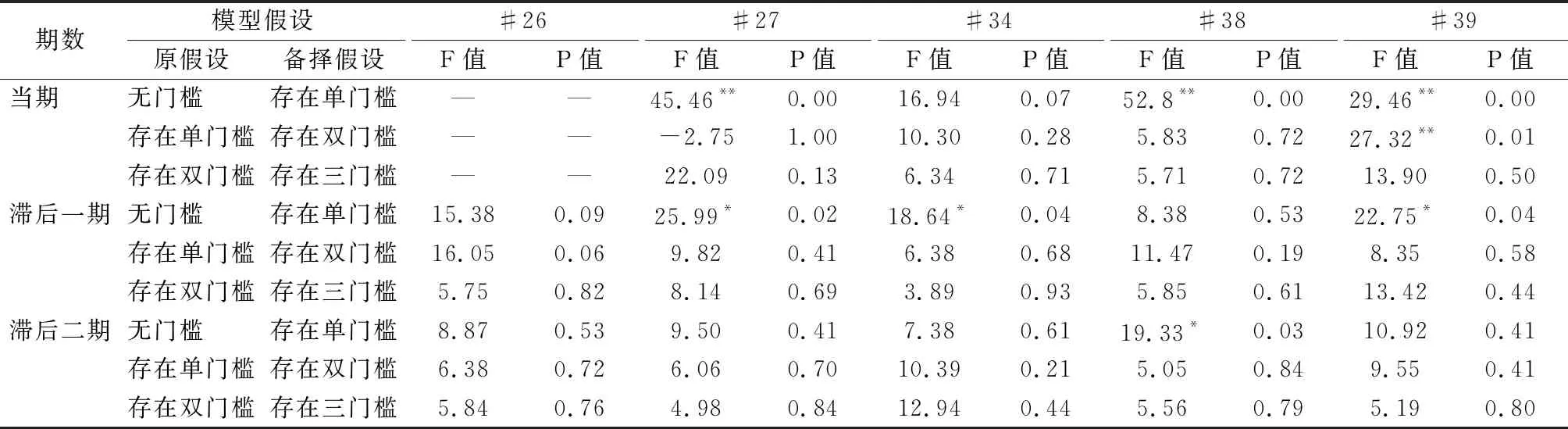
表5 研发强度门槛效应的检验结果

注：*、**分别表示在5%和1%显著性水平下显著，下同

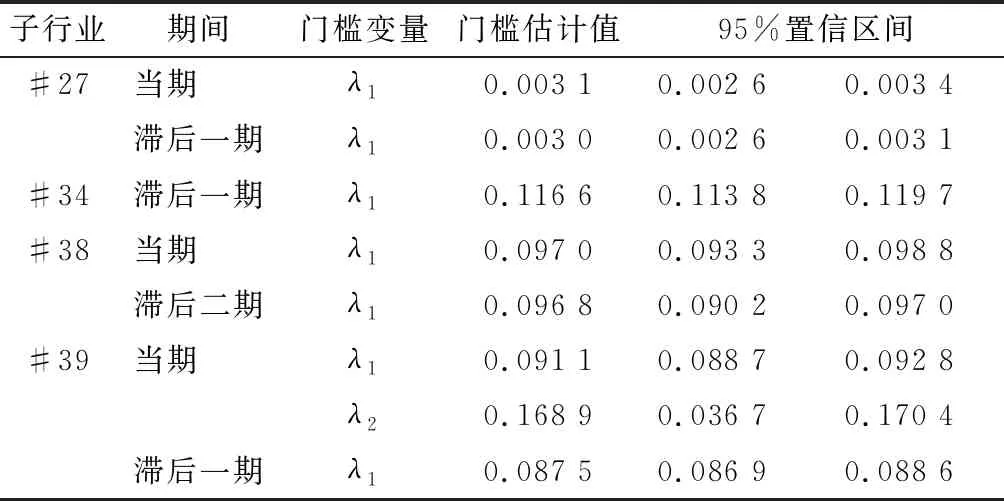
表6 门槛估计值及置信区间

3.3.2 回归结果分析

进一步对存在门槛效应的模型采用相应的面板门槛回归模型进行分析，而不存在门槛效应的模型则根据xtoverid的结果直接运用固定效应或随机效应模型。限于篇幅，表7仅列出研发强度对主营业务利润率的回归系数及相应的P值。

上述结果表明，在化学原料及化学制品制造业中，当期及滞后一期研发强度与主营业务利润率显著正相关，但滞后二期无显著关系。H2在该子行业得到验证，但H1未得到验证。

在医药制造业中，当前期，当研发强度低于0.31%时，研发投入与盈利能力显著负相关，而当超过该阈值后，两者无显著关系；滞后一期，当研发强度低于0.3%时，研发投入与盈利能力仍然负相关，而超过该值后，两者正相关。H1和H2在该子行业都得到验证。

在设备制造业中，当期及滞后二期研发强度与主营业务利润率无显著关系；对于滞后一期，当研发强度低于门槛值11.66%时，其与利润率正相关，超过该阈值后，两者无显著关系。H1和H2在该子行业得到验证。

在电气机械及器材制造业中，当前期及滞后二期研发强度均存在单门槛效应，门槛值约为9.7%，然而无论在哪个区间内，研发强度与主营业务利润率或显著负相关，或无显著关系；且滞后一期也无显著关系。该行业H1和H2都得到验证，但研发投入是负向影响。

在计算机、通信和其他电子设备制造业中，研发强度低于9.11%时，与当期利润率显著正相关，介于9.11%和16.89%时，无显著影响，超过16.89%后，产生显著的负影响。研发强度与滞后一期利润率显著正相关，且低于8.75%时所产生的积极作用更大。研发强度与滞后二期利润率正相关，回归系数减小。H1和H2都得到验证。

综合上述结果，H3得到了验证。

3.4 稳健性检验

为了检验模型的稳健性，本文将样本企业按照上市所在的证券交易所划分为两类，利用上述方法再次进行回归分析。回归得到与前文相似的结果，说明本文研究结果具有稳健性，篇幅限制省略具体结果。

4 结论与启示

本文模型分析主要结论和启示如下：

其一，不同制造业子行业的研发投入对其盈利能力的影响存在明显差异。这种差异不仅体现在有些行业研发强度与主营业务利润率间的关系是线性相关，有些是非线性相关，且相关性的方向及强弱也不一样，而且体现在研发对绩效产生影响的滞后效应及滞后期的长短也明显不同。意味着不同行业需要不同的研发投入策略。

其二，在一些制造业子行业中，研发强度与企业盈利能力存在非线性关系，研发投入存在适度区间。当研发强度过大时，研发无法对盈利能力起到积极的促进作用，甚至适得其反。比如在设备制造业中，当研发强度低于阈值11.66%时，研发投入对次年盈利能力存在积极影响，但超过临界值后，该积极影响不再显著；而在计算机、通信和其他电子设备制造业中，当研发强度低于9.11%时，研发投入正向促进企业当年盈利能力，而当其超过16.89%时，反而起到抑制作用。这要求企业应当对开展研发创新活动保持积极的态度，正确认识到从研发投资到最终提升企业绩效存在滞后性，不可急功近利。

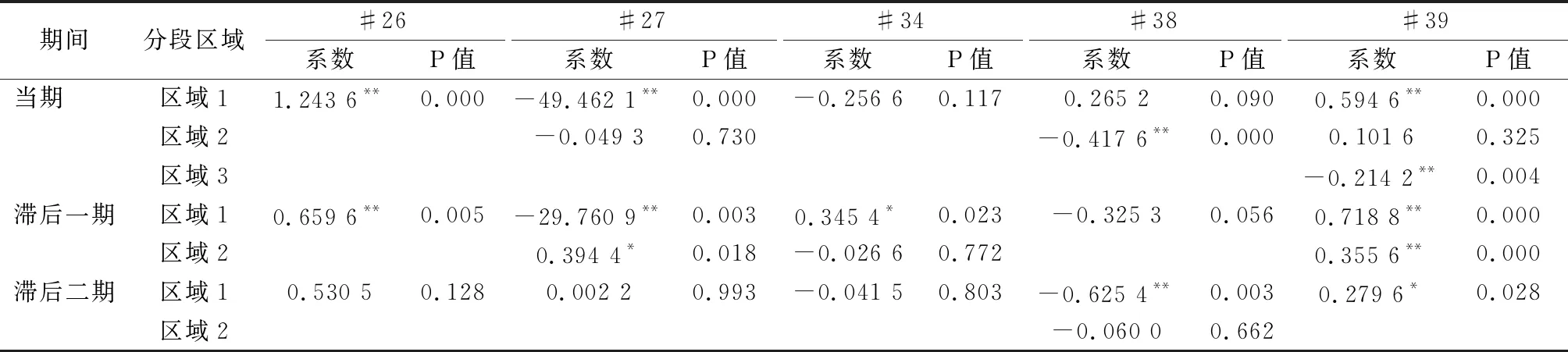
表7 研发强度对主营业务利润率的回归结果

其三，研发投入对企业盈利能力的影响存在滞后效应。在医药制造业和设备制造业中，适量研发投资需要经过一年时间转化才会对企业盈利水平起到促进作用；而在化学原料及化学制品制造业中，研发投资不仅对当年主营业务利润率具有积极影响，还会对次年盈利能力的提升起到促进作用。

最后，企业需要注重研发投入的持续性并关注关键核心技术的开发。目前我国企业研发投入对绩效产生积极影响的持续期普遍较短，一般只有1～2年。一方面，企业之间激烈的竞争导致技术更新加快，研发所带来的竞争优势难以长期维持，企业需要持续进行研发投入；另一方面，目前企业研发投入更多是一些模仿创新，而在关键核心技术开发上投入不足。虽然后者见效较慢，但研究成果难以被竞争对手模仿，能够为企业带来更为长久的竞争优势。