XPNAV-1卫星首批公开数据中光子能量对计时精度影响的统计分析

朱鸿旭，童明雷，周庆勇，李琳，蒋丰媛，韩孟纳

XPNAV-1卫星首批公开数据中光子能量对计时精度影响的统计分析

朱鸿旭1,2,3，童明雷1,2，周庆勇4,5，李琳1,2,3，蒋丰媛6，韩孟纳1,2,3

（1. 中国科学院 国家授时中心，西安 710600；2. 中国科学院 时间频率基准重点实验室，西安 710600；3. 中国科学院大学，北京 100049；4. 地理信息工程国家重点实验室，西安 710054；5. 西安测绘研究所，西安 710054；6. 大连华信计算机技术股份有限公司，大连 116085）

脉冲星导航；XPNAV-1卫星；Crab脉冲星；计时残差

0 引言

近些年来，关于毫秒脉冲星的研究正逐渐成为国际天文学界的热点[1-2]。与普通脉冲星相比，毫秒脉冲星的自转更为稳定、计时精度更高，更适合展开脉冲星计时应用方面的工作。例如：脉冲星时间尺度建立[3-5]、探测低频引力波[6-9]、测量太阳系行星质量[10]等。由于许多毫秒脉冲星在X射线波段有辐射，而且X射线探测器日趋小型化，因此毫秒脉冲星可以应用到自主导航领域。理论上，若星载原子钟精度足够高，同时观测3颗毫秒脉冲星就可以进行绝对导航。

国际上，X射线脉冲星导航的研究工作由来已久[11-13]。最近，美国NICER/SEXTANT项目开展了脉冲星导航的验证工作[14]。脉冲星导航的前景也越来越值得期待。近几年，我国在X射线脉冲星导航领域发展同样十分迅速。天宫二号搭载的POLAR、硬X射线调制望远镜（HXMT/慧眼卫星）、X射线脉冲星导航试验卫星（XPNAV-1）等平台均在进行X射线观测，开展了脉冲星导航试验，并取得了一系列进展和成果[15-17]。本文将利用XPNAV-1卫星发布的首批公开数据[18]进行计时分析。

XPNAV-1于2016年11月10日成功升空并展开观测，搭载有两套不同体制的X射线探测器：一套为采用了Wolter-I型聚焦系统的掠入射聚焦型探测器（SDD），另一套为微通道板探测器。2017年，发布了首批共35组观测数据。这批数据基于SDD的观测模式，其探测能段为0.5~10 keV，时间分辨率为1.5 μs，能量分辨率180 eV@5.9 keV。该数据时间跨度约为一个月（MJD57 709~MJD57 740），数据文件为TXT格式，包括UTC时间尺度下记录的光子到达卫星时刻，以及遥测的卫星位置与速度[16]。

1 观测光子的能量统计与处理方法

在进行区分光子能量计时精度分析前要进行预处理。在数据中，存在记录的光子能量超过量程（0.5~10 keV）的光子事件，首先要筛选掉这些光子事件。在这批数据中总计有62个光子记录的能量超过10 keV，8 253个光子记录的能量低于0.5 keV，约占光子事件总数的1.8‰。随后，将全部光子事件按照能量大小进行排序，处理得到全部光子事件的能量分位数（即指定比例排序后光子的最大能量）图，如图1所示。

图1 光子事件的能量分位数

由图1可以看出，卫星记录的低能段X射线光子远较高能段X射线光子多，考虑到探测器对不同能量光子的有效面积曲线[20]，并结合已知的幂律谱模型[21]，因而观测光子的能量分布符合理论预期。

以下本文将采用两种分段方法对光子进行分组：按光子数比例分段和按光子能量分段。在数据处理中采用DE200太阳系历表将各组光子到达航天器时刻转化为到达太阳系质心（SSB）的时刻。采用DE200历表而不是更新的历表的原因是为了保持和归算Crab脉冲星星历采用的太阳系历表一致，避免产生额外的误差[22]。对于接收高能光子的人造卫星而言，普适性的转换方程为[23]：

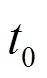
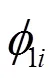
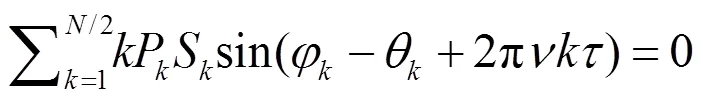
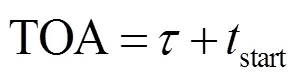
2 按光子数比例分段

根据图1可以选取占光子总数一定比例的光子。由于探测器的观测能段范围与总光子数量有限，为了使对比结果更为明显，本文分别选取以5%为间隔，能量由大到小和能量由小到大，占总数20%~50%的光子进行分析，共计7组。积分脉冲轮廓的信噪比越高，相应的TOA精度也越高。

图2至图4分别是利用全部光子进行折叠的标准脉冲轮廓，以及利用能量由小到大和能量由大到小选取的光子折叠的标准脉冲轮廓。图（a）至（g）分别表示占总数20%、25%、……、50%的光子折叠出的轮廓。

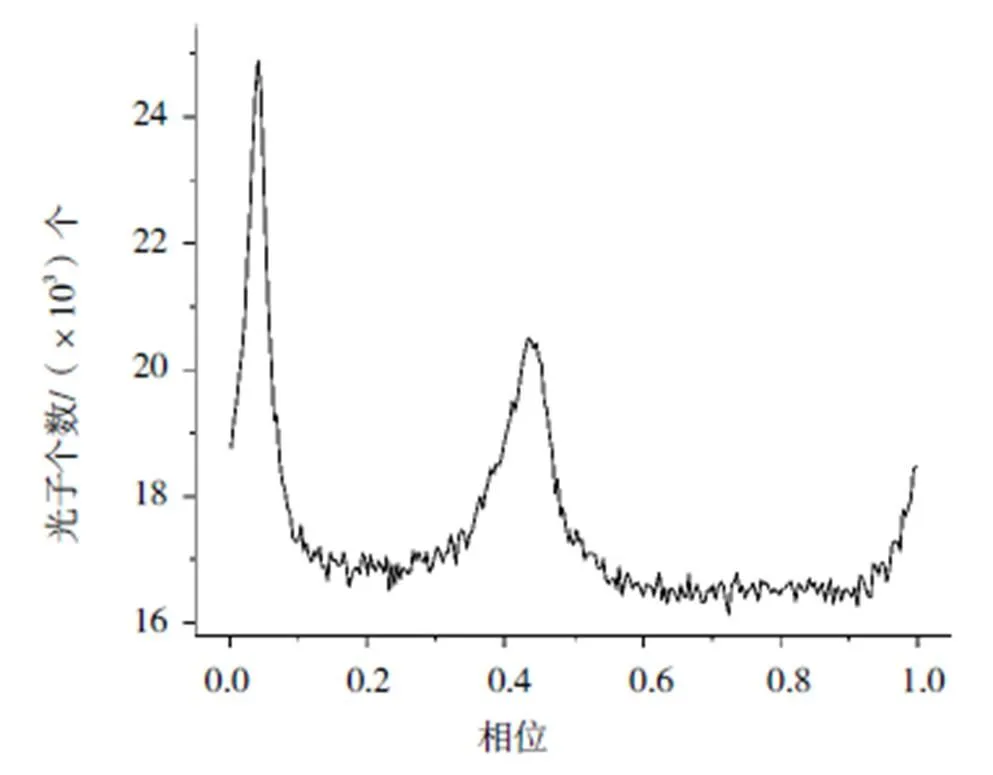
图2 所有光子的标准脉冲轮廓

由各组标准脉冲轮廓看，其与所有光子构成的标准脉冲轮廓的形状大致相同，但也有所区别。现将各组轮廓的部分特征进行分析，如表1和表2所示。

表1 能量由小到大选取光子的各组标准脉冲轮廓部分形状特征

注：50、10分别表示主、次峰附近的bin具有的光子达到其顶点光子数50%、10%的宽度，-表示主次峰之间全部bin具有的光子均大于次峰顶点光子数的10%，下同。

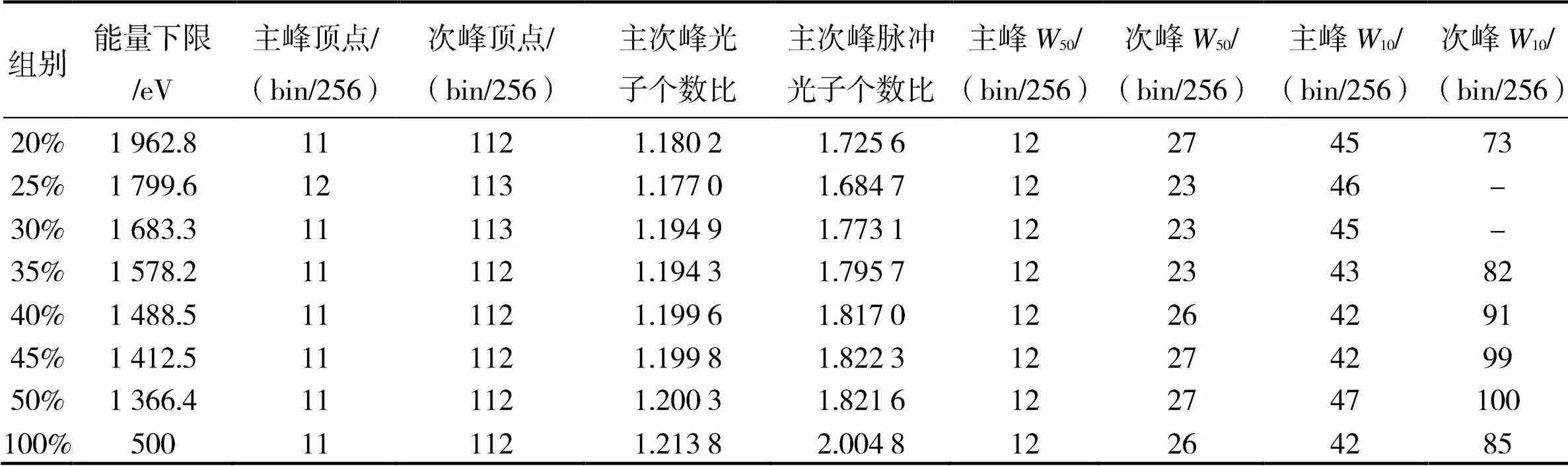
表2 能量由大到小选取光子的各组标准脉冲轮廓部分形状特征

表1和表2分别表示了不同能量的各组光子经折叠后的标准脉冲轮廓部分形状特征。其中，主次峰脉冲光子数是指将标准脉冲轮廓中主、次峰顶点所在的bin所具有的光子数分别减去标准脉冲轮廓中拥有光子数量最少的bin所具有的光子数后剩余的光子数。由于采用了基于射电波段观测数据归算的Crab脉冲星星历进行计算，因此，其主峰顶点并不位于第1个bin附近，而是有一定的距离，这个相位差称为零点相位差。由于Jodrell Bank台提供的Crab脉冲星星历给出了脉冲到达时刻，因而通过检测不同波段、不同观测时刻数据归算获得的零点相位差，有助于分析脉冲星的辐射特征，或分析不同参考钟的钟差。另外，可以看出，随着能量变化，轮廓的主峰顶点位置基本保持不变，次峰顶点的位置有随光子能量增加而远离主峰顶点的趋势。主峰的宽度似有随光子能量的增加增宽的趋势，而次峰的宽度由现有的数据很难看出有着明显的规律。同时，随着光子能量的增加，轮廓的次峰有着明显的升高。在测量TOA时，是以主峰顶点为参考点。因此，主峰位置和宽度的变化将分别导致零点相位差的变化和TOA测量精度的变化。零点相位差的不变性非常重要，因为它代表了系统误差。综上所述，Crab脉冲星的标准脉冲轮廓的形状与折叠轮廓采用的光子能段有关。显然，当折叠轮廓选用的光子能段更接近时，更有利于折叠出高信噪比的脉冲轮廓。

图5 能量由小到大选取光子的各组计时残差与TOA测量精度特征

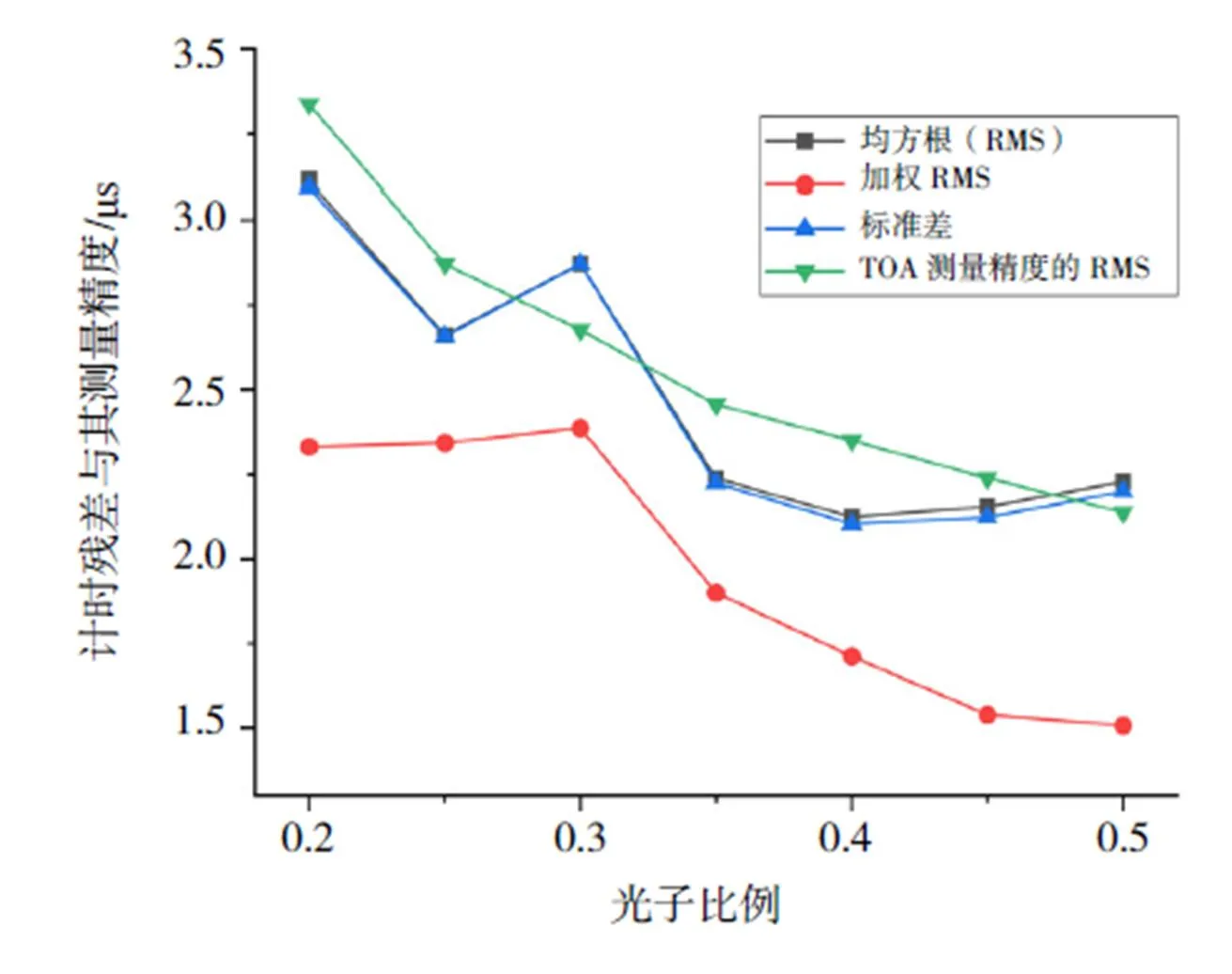
图6 能量由大到小选取光子的各组计时残差与TOA测量精度特征

3 按光子能量分段

相较按照比例选取光子进行计算，按照能量范围选取光子进行计算更具有实际指导意义。本文将XPNAV-1卫星的观测能段（0.5~10 keV）由小到大划分为4个能量区间，其中前3个区间的能量涵盖范围均为500 eV。而能量大于2 000 eV的光子数量有限，难以按照500 eV的间隔进行划分，故将其作为一个能量区间，如表3所示。

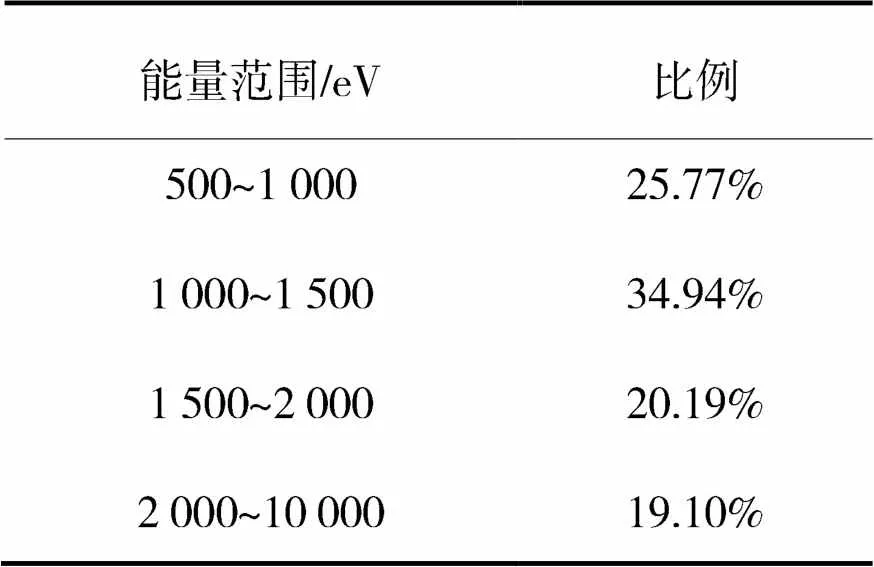
表3 不同能量区间光子所占比例

按照表3划分的能量区间，重复上述处理过程，得到各组的标准脉冲轮廓及其特征，和计时残TOA测量精度特征，如图7、表4和图8所示。

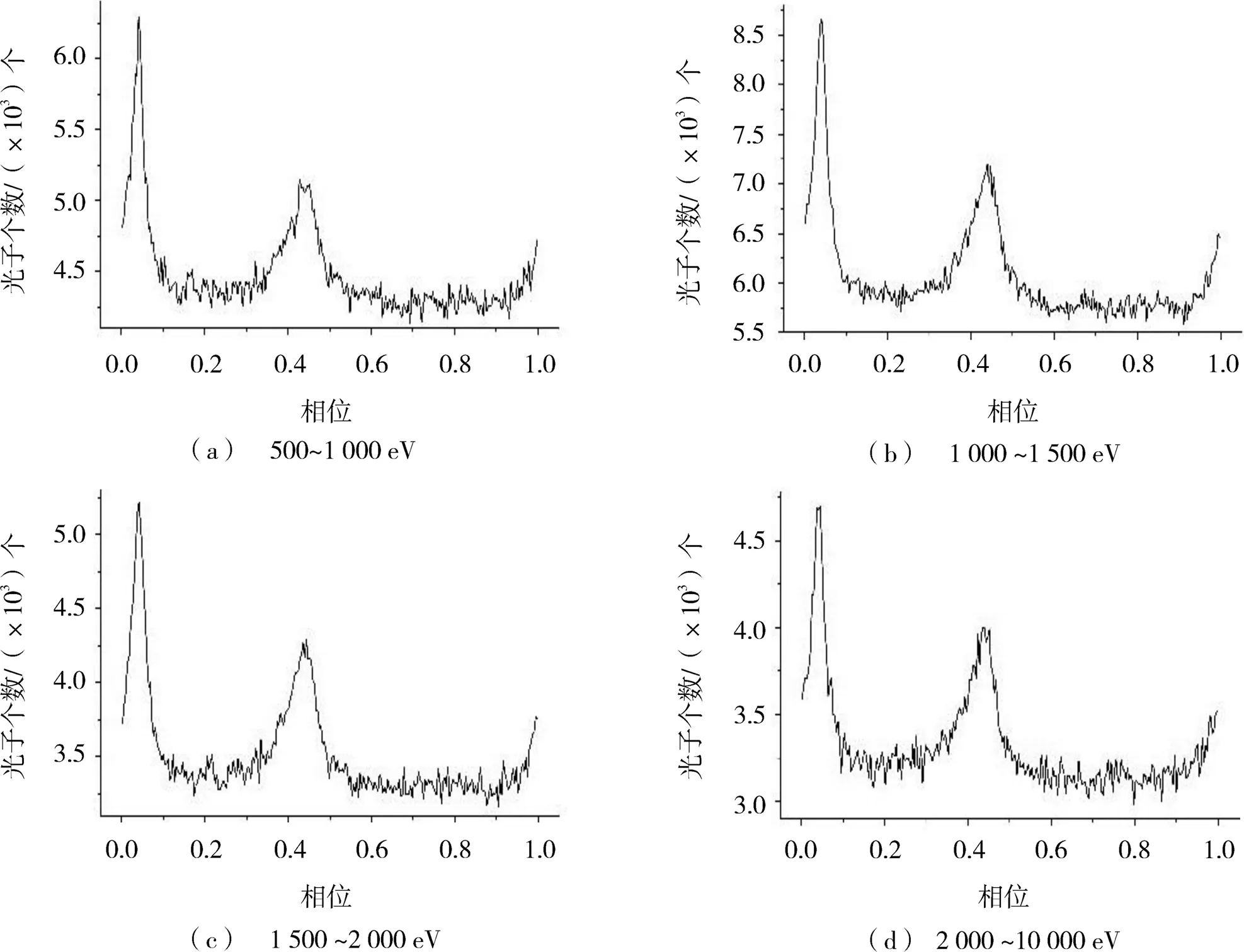
图7 不同能量区间光子的各组标准脉冲轮廓

表4 不同能量区间光子的各组标准脉冲轮廓部分形状特征

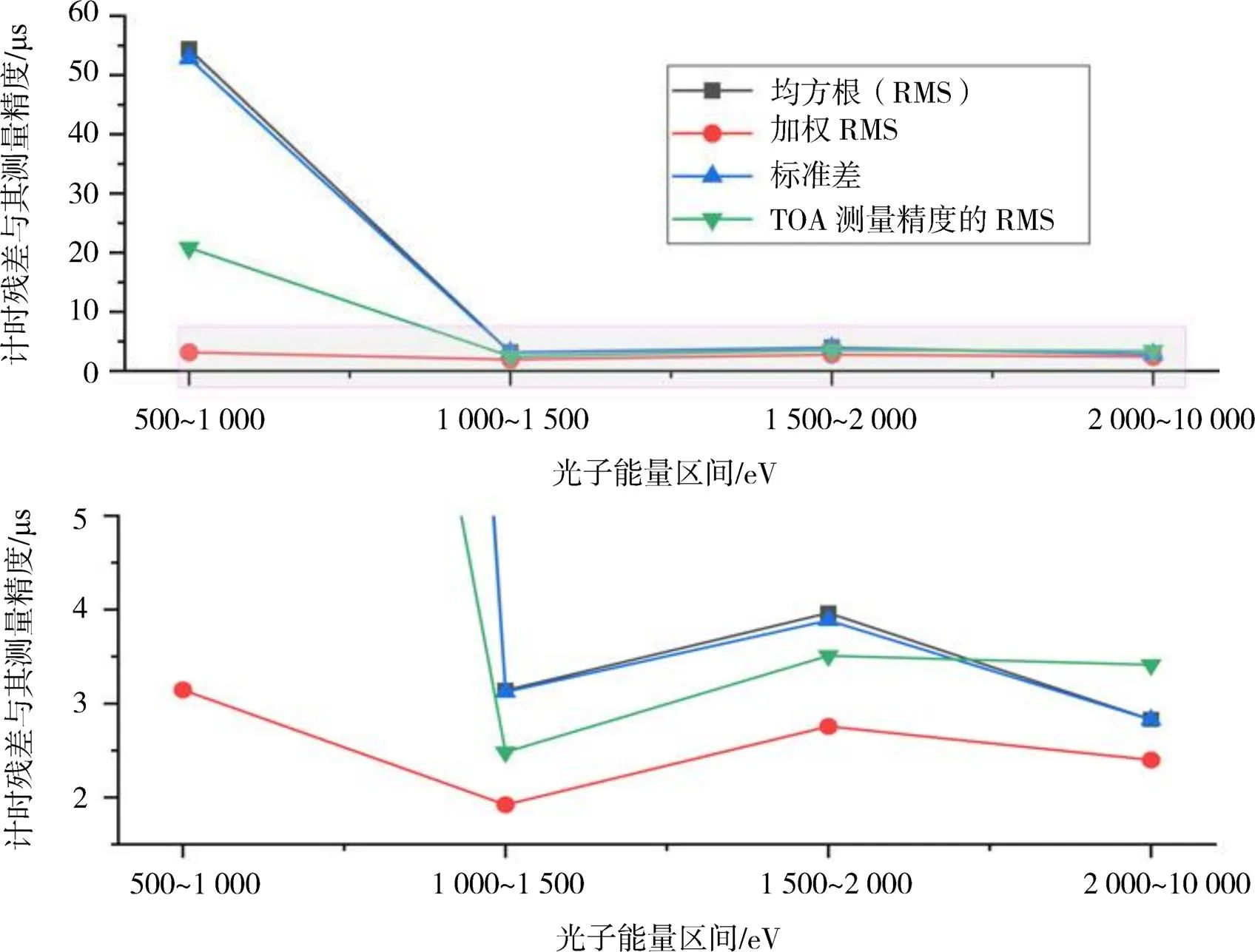
图8 不同能量区间光子的各组计时残差与TOA测量精度特征

从表4可以看出，不同能量范围光子标准脉冲轮廓的形状特征与表2和表3体现的特征一致性较强，尤其是次峰顶点位置与次峰高度的变化趋势较为明显。主峰顶点在最高频时有些许变化，这与表2的结果具有一致性。由于数据量有限，较难给出零点相位差与光子能量的确切关系。而从图8可以看出，高能光子在光子总数较少，涵盖了较宽的能段（不利于折叠出高信噪比的轮廓）的情况下，仍能保持和低能光子大致相当的噪声水平。说明在接收高能光子时，增加较少数量的光子即对轮廓的信噪比改善明显。考虑到探测器在接收较高能段X射线光子时，有效面积非常有限而影响接收，且脉冲星辐射的较高能段的X射线光子数量本就少于较低能段的X射线光子。结合第2节的内容，本文建议在今后设计以脉冲星计时与导航为观测目的X射线星载探测器时，应尽量考虑较高能段的X射线光子的探测效果。同时在制定观测方案时，要尽可能避开可能对接收较高能段的X射线光子存在干扰的时段。

4 结语

本文对XPNAV-1卫星目前公开的35组Crab脉冲星观测数据，根据不同的光子比例和光子能量，将其划分为不同的组。利用DE200历表与英国Jodrell Bank台发布的Crab脉冲星星历进行折叠轮廓，并采用Taylor傅里叶相关法进行相关计算。得到了各组的标准脉冲轮廓部分形状特征，以及计时残差和TOA测量精度特征。经过分析，得到了Crab脉冲星在卫星观测能段范围内的轮廓变化趋势和计时残差变化趋势。另外，从目前的数据来看，各组计算零点相位差基本不变。本文认为，尽管Crab脉冲星辐射的较高能段的X射线光子比较低能段的X射线光子少，但较高能段的X射线光子观测数据可能更适合用于脉冲星计时与导航。

由于数据有限，很难将光子细分成更多的组。这也导致产生了标准脉冲轮廓的一些形状特征不明显或难以分析，相关计算后的计时残差分析结果也存在波动的情况。这些问题和其他更细致的分析计算有待更多数据公开后加以解决。

[1] ARCHIBALD A M, GUSINSKAIA N V, HESSELS J W T, et al. Universality of free fall from the orbital motion of a pulsar in a stellar triple system[J]. Nature, 2018, 559(7712): 73-76.

[2] PORAYKO N K, ZHU Xing-jiang, LEVIN Y, et al. Parkes pulsar timing array constraints on ultralight scalar-field dark matter[J]. Physical Review D, 2018, 98(10): 2002.

[3] PETIT G, TAVELLA P. Pulsars and time scales[J]. Astronomy and Astrophysics, 1996(308): 290-298.

[4] 赵成仕, 高玉平, 童明雷. 天然时钟——脉冲星时间尺度[J]. 科学, 2018, 70(5): 44-47.

[5] HOBBS G, COLES W, MANCHESTER R N, et al. Development of a pulsar-based time-scale[J]. Monthly Notices of the Royal Astronomical Society, 2012, 427: 2780-2787.

[6] HELLINGS R W, DOWNS G S. Upper limits on the isotropic gravitational radiation background from pulsar timing analysis[J]. The Astrophysical Journal, 1983, 265: 39-42.

[7] JENET F A, HOBBS G B, LEE K J, et al. Detecting the stochastic gravitational wave background using pulsar timing[J]. The Astrophysical Journal, 2005, 625: 123-126.

[8] HOBBS G, ARCHIBALD A, ARZOUMANIAN Z, et al. The international pulsar timing array project: using pulsars as a gravitational wave detector[J]. Classical and Quantum Gravity, 2010, 27(8): 4013.

[9] TONG Ming-lei, DING Yong-heng, ZHAO Cheng-shi, et al. Imprints of relic gravitational waves on pulsar timing[J]. Research in Astronomy and Astrophysics, 2016, 16(3): 49.

[10] CHAMPION D J, HOBBS G B, MANCHESTER R N, et al. Measuring the mass of solar system planets using pulsar timing[J]. The Astrophysical Journal Letters, 2010, 720(2): 201-205.

[11] 李连升, 梅志武, 吕政欣, 等. X射线脉冲星导航探测技术发展综述[J]. 兵器装备工程学报, 2017, 38(5): 1-9.

[12] SHEIKH S I. The use of variable celestial X-ray sources for spacecraft navigation[D]. Maryland: University of Maryland, 2005.

[13] SALA J, URRUELA A, VILLARES X, et al. Feasibility study for a spacecraft navigation system relying on pulsar timing information[R]. [S.l]: the Advanced Concepts Team, European Space Agency, 2004.

[14] ALEXANDRA W. NASA test proves pulsars can function as a celestial GPS[J]. Nature, 2018(553): 261-262.

[15] 郑世界, 葛明玉, 韩大炜, 等. 基于天宫二号POLAR的脉冲星导航实验[J]. 中国科学(物理学 力学 天文学), 2017, 47(9): 120-128.

[16] 帅平, 张新源, 黄良伟, 等. 脉冲星导航试验卫星科学观测数据分析[J]. 空间控制技术与应用, 2017, 43(2): 1-6.

[17] LI Ti-pei, XIONG Shao-lin, ZHANG Shuang-nan, et al. Insight-HXMT observations of the first binary neutron star merger GW170817[J]. Science China (Physics, Mechanics & Astronomy), 2018, 61(3): 30-37.

[18] 黄良伟, 刘群, 帅平, 等. XPNAV-1卫星科学试验任务[DB/OL]. (2017-08-28)[2019-01-02]. http://www.qxslab.cn/Upload/201708/20170828145223_4814.pdf.

[19] 杨廷高, 童明雷, 高玉平. 毫秒脉冲星计时噪声估计[J]. 时间频率学报, 2014, 37(2): 80-88.

[20] 张大鹏, 王奕迪, 姜坤, 等. XPNAV-1卫星实测数据处理与分析[J]. 宇航学报, 2018, 39(4): 411-417.

[21] THOMPSON C, LYUTIKOV M, KULKARNI S R. Electrodynamics of magnetars: implications for the persistent X-ray emission and spin-down of the soft Gamma repeaters and anomalous X-ray pulsars[J]. The Astrophysical Journal, 2002, 574(1): 332-355.

[22] 朱幸芝, 童明雷, 赵成仕, 等. 历表误差对脉冲星计时残差空间相关性影响的研究[J]. 天文学报, 2017, 58(6): 20-29.

[23] EDWARDS R T, HOBBS G B, Manchester R N. TEMPO2, a new pulsar timing package-II. The timing model and precision estimates[J]. Monthly Notices of the Royal Astronomical Society, 2006, 372(4): 1549-1574.

[24] 周庆勇, 姬剑锋, 任红飞. X射线脉冲星自主导航的观测方程[J]. 物理学报, 2013, 62(13): 586-595.

[25] 童明雷, 杨廷高, 赵成仕, 等. 脉冲星计时模型参数的测量精度分析与估计[J]. 中国科学(物理学 力学 天文学), 2017, 47(9): 9503.

[26] 赵成仕, 童明雷, 高玉平, 等. 脉冲星钟模型精度分析[J]. 天文学报, 2017, 58(3): 61-69.

[27] 杨廷高, 童明雷, 赵成仕, 等. Crab脉冲星X射线计时观测数据处理与分析[J]. 天文学报, 2018, 59(2): 10-16.

[28] TAYLOR J H. Pulsar timing and relativistic gravity[J]. Philosophical Transactions: Physical Sciences and Engineering, 1992, 341(1660): 117-134.

[29] 童明雷, 丁勇恒, 赵成仕, 等. 引力波引起的脉冲星计时残差模拟与分析[J]. 时间频率学报, 2015, 38(1): 44-51.

Statistical analysis of the influences of photon energy on timing accuracy in the first public data release of XPNAV-1 satellite

ZHU Hong-xu1,2,3, TONG Ming-lei1,2, ZHOU Qing-yong4,5, LI Lin1,2,3, JIANG Feng-yuan6, HAN Meng-na1,2,3

(1. National Time Service Center, Chinese Academy of Sciences, Xi’an 710600, China;2. Key Laboratory of Time and Frequency Primary Standards, Chinese Academy of Sciences, Xi’an 710600, China;3. University of Chinese Academy of Sciences, Beijing 100049, China;4. State Key Laboratory of Geo-information Engineering, Xi’an 710054, China;5. Xi’an Research Institute of Surveying and Mapping, Xi’an 710054, China;6. Dalian Hi-Think Computer Technology, Corporation., Dalian 116085, China)

pulsar navigation; XPNAV-1 satellite; Crab pulsar; timing residual

10.13875/j.issn.1674-0637.2020-01-0029-12

2019-07-09；

2019-08-30

国家自然科学基金资助项目（U1831130；U1531112）；中国科学院青年创新促进会资助项目（2017450）；中国科学院“西部之光”人才培养计划资助项目（A类）（XAB2015A06）

朱鸿旭，男，硕士，主要从事脉冲星计时及其导航应用研究。