基于光晶格钟的自旋轨道耦合简介

王林雪，郭慧，刘涛，张晓斐

基于光晶格钟的自旋轨道耦合简介

王林雪1,2,3，郭慧1,2,3，刘涛1,2,3，张晓斐1,2,3

（1.中国科学院 国家授时中心，西安 710600；2.中国科学院 时间频率基准重点实验室，西安 710600；3. 中国科学院大学 天文与空间科学学院，北京 101048）

基于光晶格原子钟实现人造自旋轨道耦合的相关研究进展，简要说明利用光晶格原子钟实现自旋轨道耦合的基本原理。通过与传统实现自旋轨道耦合的拉曼耦合方案相比较，指出利用光晶格原子钟实现自旋轨道耦合方案的优越性。讨论了自旋轨道耦合光晶格原子钟在量子简并区域可能实现的奇异物态和新奇量子现象。强调了光钟平台在超冷原子新物态的制备、操控和测量等方面扮演的重要角色。

光晶格原子钟；自旋轨道耦合；超冷原子气体；新奇量子态

0 引言

光钟是以光学波段的量子跃迁作为频率标准的高精度时间测量工具[1]。光晶格原子钟[2-3]作为光钟的一种，其频率稳定度和不确定度已达到10-19量级[4]，是目前性能指标最高的原子钟，有望替代铯原子喷泉钟成为新一代秒定义的基准钟[5-6]。

光钟不但提供高精度的时间频率信号，而且光钟系统本身也是一个人类测量精度极高的科学与技术研究平台，在高精度测量和基础物理学方面有重要应用。可用于精密测量光学跃迁的同位素频移[7]进而检验标准模型的正确性，探测超越标准模型的新粒子和相互作用[8]；可用于万有引力常数、精细结构常数、质子电子质量比等基本物理常数的测定[9-11]；还可用于验证洛伦兹协变[12-13]和探测暗物质[14]等。随着光钟技术的不断发展，光晶格原子钟的应用范围已经不限于测量领域，还可以用于设计和操控新的量子系统，成为超冷原子量子模拟的新工具。

近年来，超冷原子物理的研究加深了人们对物质结构、光与物质相互作用和基本物理规律的认识[15]。超冷原子物理研究之所以能取得重大成功，依赖于其在几个方面的实验突破，主要包括通过Feshbach共振技术调节原子间的相互作用[16-17]、通过光晶格技术实现各种凝聚态物理模型[18-20]、利用人造自旋轨道耦合实现各种奇异拓扑量子态[21-25]。

人造自旋轨道耦合是利用激光[26-29]、磁场脉冲[30-32]等手段，将原子的内部自旋态和其外部轨道运动耦合起来。超冷原子自旋轨道耦合的实验实现[26-29, 32-34]，一方面突破了凝聚态系统内中性原子无法模拟带电粒子在电磁场中的响应这一瓶颈，拓展了超冷量子气体作为量子模拟平台的适用范围；另一方面为实现一系列前所未有的全新物理模型提供了可能，为发现新物态和探索奇异量子现象开辟了道路。

然而，随着自旋轨道耦合物理研究的不断深入，新的自旋轨道耦合形式的实验实现面临一些困难和挑战。通常自旋轨道耦合的实验方案，是在超冷碱金属原子气体中，通过双光子拉曼过程将原子的2个或3个超精细能级和高激发态耦合实现的[26-29, 35]。该方案中拉曼激光的单光子失谐受限于激发态能级的精细结构劈裂[35]。由于碱金属原子激发态精细结构能级劈裂较小，使得系统不可避免地遭受了自发辐射引起的加热效应。

自发辐射引起的加热效应的存在，一方面使得系统的寿命比较短，因而当前有关超冷原子自旋轨道耦合的实验研究大都局限于单粒子、平均场水平，限制了在超越平均场水平上、更长时间尺度上对系统量子多体动力学性质的研究；另一方面对于复杂的自旋轨道耦合形式，如二维和三维自旋轨道耦合[36-38]、具有SU（3）对称的自旋轨道耦合[39]等，由于需要引入更多的激光，相关实验面临严峻的挑战。目前几乎所有自旋轨道耦合的实验大都局限在一维情况，只有少数几个实验实现了二维形式的自旋轨道耦合[33-34]。

如何有效避免自发辐射引起的加热效应，是当前超冷原子自旋轨道耦合物理研究的重要问题。最近美国国家标准和技术研究院叶军研究组等从理论上提出、并在实验上实现了基于光晶格原子钟的人造自旋轨道耦合[40-44]。为突破超冷原子物理自旋轨道耦合研究的瓶颈开辟了新的道路。本文将基于最近的理论和实验进展，简要说明利用光晶格原子钟实现自旋轨道耦合的基本原理，介绍光钟在超冷原子新物态的制备、操控和测量等方面扮演的重要角色，并讨论其在超冷原子前沿科学研究领域可能的应用。

1 基于光晶格原子钟实现自旋轨道耦合的基本原理

在传统的超冷碱金属原子气体中实现自旋轨道耦合的方案中，由于受到加热效应的影响，使系统的寿命比较短，限制了自旋轨道耦合相关研究的发展。随后，对于激发态精细结构劈裂较大的碱土金属相关研究便引起了大家的注意，并且随着光晶格原子钟的不断发展，给研究自选轨道耦合带来了新的研究方向。

1.1 基于光晶格原子钟实现一维自旋轨道耦合

为了有效抑制自发辐射引起的加热效应，科学家提出可以选择激发态精细结构劈裂较大或激发态寿命较长的碱土类金属原子[24, 40, 45-47]。2016年，叶军研究组从理论上指出可以在光晶格原子钟的钟态上，利用钟探测激光的Rabi跃迁实现自旋轨道耦合。下面我们对相关的基本原理作简要介绍。

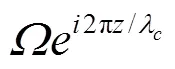
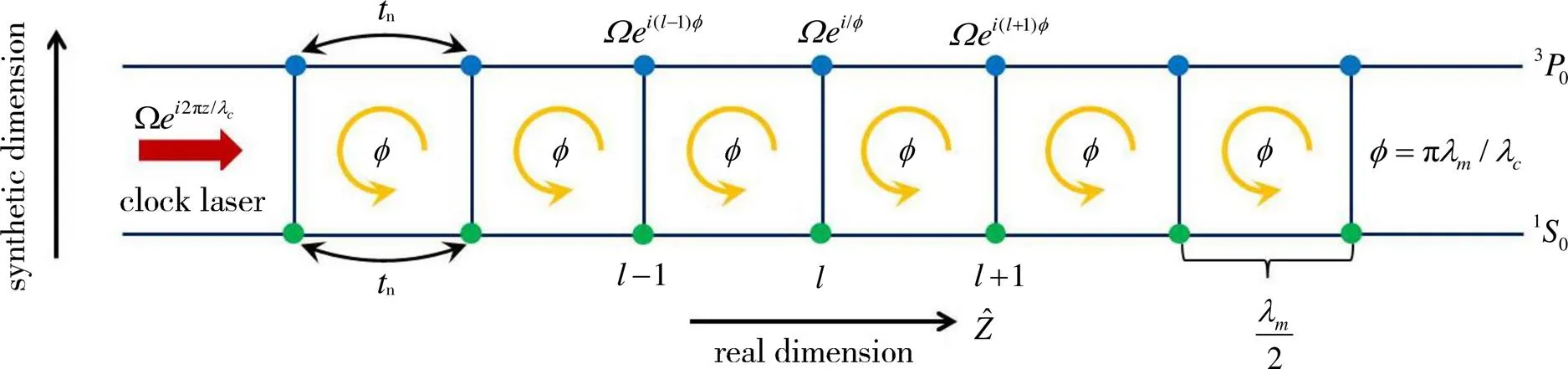
图1 基于光晶格钟实现自旋轨道耦合的原理图

1.2 基于光晶格原子钟实现高维自旋轨道耦合

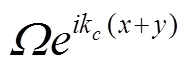
图2 基于光晶格钟实现二维自旋轨道耦合的钟探测激光几何结构示意图

1.3 基于光晶格原子钟实现自旋轨道耦合的优越性

跟拉曼激光耦合方案相比，利用光晶格原子钟实现自旋轨道耦合的优越性主要表现在以下几个方面。① 有效避免了自发辐射引起的加热效应，相比于碱金属原子，类碱土金属原子的激发态精细结构能级劈裂值较大，能有效地避免失谐带来的加热效应[35]。② 所用的激光频率更为单一，仅需要用到魔术波长激光和钟探测激光两个频率的激光。更少的激光束可以最大限度地避免干涉引起的不稳定性[42]。③ 光钟系统为研究自旋轨道耦合的物理性质提供了先进的精密测量手段。例如可通过Rabi和Ramsey谱线[40, 44]实现对原子自旋动力学实时、无破坏性的测量。

2 量子简并区域的自旋轨道耦合效应

光晶格原子钟的实验研究已经进入到量子简并区域[55]。费米简并三维光钟[55]的实验实现一方面有利于光钟性能的进一步提高，另一方面也为实现更高维度[36-38, 41]和更高对称性的自旋轨道耦合形式[39]开辟了道路。当光晶格原子钟在量子简并区域运行时，Rabi和Ramsey光谱法的观测和操控的灵敏度和适用性将会明显提高。基于光钟的高精度光谱测量技术和最近超冷原子系统中发展的高空间分辨率的投影技术[56-58]以及磁感相位比对技术[59-60]，为发现和观测新的奇异量子态和奇异量子现象提供了有力的实验技术支持。

通过调节钟探测激光的偏振，可以实现不同超精细能级之间的耦合[42]，进而可以实现多维的人造晶格[61]。此时自旋轨道耦合等效于人造维度上的有效相干隧穿。通过轨道Feshbach技术[62-64]可调节钟态上轨道间的自旋交换相互作用，进而可以实现各种类型的量子多体自旋模型。这使我们可以基于光晶格原子钟研究各种低温量子磁性[65]、强关联量子态[66]、拓扑超流态[67]、Weyl半金属态[41]、手性边缘态[42-43]以及BEC-BCS渡越区域的新奇量子效应等。

基于光晶格原子钟可研究具有SU（）对称的碰撞相互作用[68]的超冷原子系统的性质。与此同时，如何借助光钟系统实现具有SU（）对称的自旋轨道耦合是一个有趣的科学问题。最近 Ketterle 研究组在SU（2）自旋轨道耦合系统中实验观测到具有超固性质的条纹相[69-71]，标志着超固现象研究的突破性进展。然而Ketterle等观察到的条纹相只在一个方向上破缺了系统的平移对称性。我们先前的工作[72]已经指出，SU（3）自旋轨道耦合引起的三阱色散关系，可产生在二维动量空间三点凝聚的二维晶格相。不同于Ketterle观察到的条纹相，该晶格相在两个方向上同时破缺了系统的平移对称性。下一步，我们将研究如何借助光钟的优势平台设计合适的自旋轨道耦合形式，进而实现在三个方向上同时破缺系统平移对称性的超固相。

3 结语

本文简述了基于光晶格原子钟实现自旋轨道耦合的实验方案，并讨论了光晶格原子钟在量子简并区域可能实现的各种奇异物态和奇异量子现象。光钟技术的不断发展进步，为超冷量子气体研究提供了新的实验研究平台和高超的精密测量手段。而对于超冷量子系统物理性质的研究，如何反过来推动光钟技术的发展进步，是一个重要的开放性课题。

[1] LUDLOW A D, BOYD M M, YE J, et al. Optical atomic clocks[J]. Reviews of Modern Physics, 2015, 87(2): 637-701.

[2] KATORI H. Optical-lattice clock sets new standard for timekeeping[J]. Physics Today, 2014, 67(3): 2294-2296.

[3] DEREVIANKO A, KATORI H. Colloquium: physics of optical lattice clocks[J]. Reviews of Modern Physics, 2011(83): 331.

[4] GREW W M, ZHANG X, FASANO R J, et al. Atomic clock performance enabling geodesy below the centimeter level[J]. Nature, 2018(564): 87-90.

[5] GREBING C, AI-MASOUDI A, DORSCHER S, et al. Realization of a timescale with an accurate optical clock[J]. Optica, 2015(3): 563.

[6] HACHISU H, NAKAGAWA F, HANADO Y, et al. Months-long real-time generation of a time scale based on an optical clock[J]. Scientific Reports, 2018, 8(1): 4243-4247.

[7] TAKANO T, MIZUSHIMA R, KATORI H. Precise determination of the isotope shift of Sr-88-Sr-87 optical lattice clock by sharing perturbations[J]. Applied Physics Express, 2017, 10(7): 2801.

[8] DELAUNAY C, OZERI R, PEREZ G, et al. Probing atomic higgs-like forces at the precision frontier[J]. Physical Review D, 2017, 96(9): 3001.

[9] ROSENBAND T, HUME D B, SCHMIDT P O, et al. Frequency ratio of Al+ and Hg+ single-ion optical clocks; metrology at the 17th decimal place[J]. Science, 2008, 319(5871): 1808-1819.

[10] GODUN R M, NISBET-JONES P B R, JONES J M, et al. Frequency ratio of two optical clock tranditions in171Yb+and constraints on the time variation of fundamental[J]. Physical Review Letters, 2014, 113(21): 801.

[11] HUNTEMANN N, LIPPHARDT B, TAMM C, et al. Improved limit on a temporal variation ofm/mfrom comparisons of Yb+and Cs atomic clocks[J]. Physical Review Letters, 2014, 113(21): 802.

[12] TOBAR M E, STANWIX P L, MCFERRAN J J M, et al. Testing local position and fundamental constant invariance due to periodic gravitational and boost using long-term comparision of the SYRTE atomic fountains and H-masers[J]. Physical Review D, 2013, 87(12): 2004.

[13] DELVA P, LODEWYCK J, BILICKI S, et al. Test of special relativity using a fiber network of optical clocks[J]. Physical Review Letters, 2017, 118(22): 1102.

[14] DEREVIANKO A, POSPELOV M. Hunting for topological dark matter with atomic clocks[J]. Nature Physics, 2014(10): 933-936.

[15] YE J. Preface: special topic on cold atoms[J]. National Science Review,2016(3): 165.

[16] GRIMN R, JULIENNE P. Feshbach resonances in ultracold gases[J]. Reviews of Modern Physics, 2010(82): 1225.

[17] KÖHLER T, GÓRAL K. Production of cold molecules via magnetically tunable Feshbach resonances[J]. Reviews of Modern Physics, 2006(78): 1311.

[18] BLOCH I. Many-body physics with ultracold gases[J]. Reviews of Modern Physics, 2008(80): 885.

[19] MORSCH O. Dynamics of Bose-Einstein condensates in optical lattices[J]. Reviews of Modern Physics, 2006(78): 179.

[20] LEWENSTEIN M, SANPERA A, AHUFINGER V, et al. Ultracold atomic gases in optical lattices: mimicking condensed matter physics and beyond[J]. Advances in Physics, 2007, 56(2): 243-379.

[21] GALITSKI V, SPIELMAN I B. Spin-orbit coupling in quantum gases[J]. Nature, 2013(49): 49-54.

[22] MANCHON A, KOO H C, NITTA J, et al. New perspectives for Rashba spin-orbit coupling[J]. Nature Materials, 2015, 14(9): 871-882.

[23] GOLDMAN N, JUZELIUNAS G, OHBERG P, et al. Light-induced gauge fields for ultracold atoms[J]. Reports on Progress in Physics, 2014, 77(12): 6401.

[24] DALIBARD J, GERBIER F, JUZELIUNAS G, et al. Colloquium: artificial gauge potentials for neutral atoms[J]. Reviews of Modern Physics, 2011, 83(4): 1523.

[25] WEI Y, ZHANG W, CUI X. Pairing superfluidity in spin-orbit coupled ultracold Fermi gases[J]. Science China (Physics, Mechanics & Astronomy), 2015(58): 1-11.

[26] LIN Y J, JIMÉNEZ-GARCÍA K, SPIELMAN I B. Spin-orbit-coupled Bose-Einstein condensates[J]. Nature, 2011, 471(7336): 83-88.

[27] ZHANG J Y, JI S C, CHEN Z, et al. Collective dipole oscillations of a spin-orbit coupled Bose-Einstein condensat[J]. Physical Review Letters, 2012, 109(11): 5301.

[28] WANG P, YU Z Q, FU Z, et al. Spin-orbit coupled degenerate Fermi gases[J]. Physical Review Letters, 2012, 109(9): 5301.

[29] CHEUK L W, SOMMER A T, HADZIBABIC Z, et al. Spin-injection spectroscopy of a spin-orbit coupled Fermi gas[J]. Physical Review Letters, 2012, 109(9): 5302.

[30] XU Z F, YOU L, UEDA M. Atomic spin-orbit coupling synthesized with magnetic-field-gradient pulses[J]. Physical Review A, 2013, 87(6): 3634.

[31] ANDERSON B M, SPIELMAN I B, JUZELIŪNAS G. Magnetically generated spin-orbit coupling for ultracold atoms[J]. Physical Review Letters, 2013, 111(12): 5301.

[32] LUO X, WU L, CHEN J, et al. Tunable atomic spin-orbit coupling synthesized with a modulating gradient magnetic field[J]. Scientific Reports, 2016(6): 18983.

[33] HUANG L, MENG Z, WANG P, et al. Experimental realization of two-dimensional synthetic spin-orbit coupling in ultracold Fermi gases[J]. Nature Physics, 2016(12): 540.

[34] WU Z, ZHANG L, SUN W, et al. Realization of two-dimensional spin-orbit coupling for Bose-Einstein condensates[J]. Science, 2016, 354(6308): 83-88.

[35] SPIELMAN I B. Raman processes and effective gauge potenticals[J]. Physical Review A, 2009, 79(6): 3613.

[36] JUZELIUNAS G, RUSECKAS J, DALIBARD J. Generalized rashba-dresselhaus spin-orbit coupling for cold atoms[J]. Physical Review A, 2010, 81(5): 3403.

[37] CAMPBELL D L, JUZELIUNAS G, SPIELMAN I B. Realistic rashba and dresselhaus spin-orbit coupling for neutral atoms[J]. Physical Review A, 2011, 84(2): 5602.

[38] ANDERSON B M, JUZELIUNAS G, GALITSKI V M, et al. Synthetic 3D spin-orbit coupling[J]. Physical Review Letters, 2012, 108(23): 5301.

[39] BARNETT R, BOYD G R, GALITSKI V. SU(3) spin-orbit coupling in systems of ultracold atoms[J]. Physical Review Letters, 2012, 109(23): 5308.

[40] WALL M L, KOLLER A P, LI S, et al. Synthetic spin-orbit coupling in an optical lattice clock[J]. Physical Review Letters, 2016, 116(3): 5301.

[41] ZHOU X, LUO X W, CHEN G, et al. Rashba and Weyl spin-orbit coupling in an optical lattice clock[DB/OL]. (2019-01-11)[2019-02-26] https://arxiv.org/abs/1804.09282.

[42] LIVI L F, CAPPELLINI G, DIEM M, et al. Synthetic dimensions and spin-orbit coupling with an optical clock transition[J]. Physical Review Letters, 2016, 117(22): 401.

[43] KOLKOWITZ S, BROMLEY S L, BOTHWELL T, et al. Spin-orbit-coupled fermions in an optical lattice clock[J]. Nature, 2017(542): 66-70.

[44] BROMLEY S L, KOLKOWITZ S, BOTHWELL T, et al. Dynamics of interacting fermions under spin-orbit coupling in an optical lattice clock[J]. Nature Physics, 2018(14): 399.

[45] CUI X, LIAN B, HO T L, et al. Synthetic gauge eld with highly magnetic lanthanide atoms[J]. Physical Review A, 2013, 88(11): 601.

[46] BURDICK N Q, TANG Y, LEV B L. Long-lived spin-orbit-coupled degenerate dipolar Fermi gas[J]. Physical Review X, 2016(3): 1022.

[47] MANCINI M, PAGANO G, CAPPELLINI G, et al. Observation of chiral edge states with neutral fermions in synthetic Hall ribbons[J]. Science, 2015, 349(6255): 1510-1512.

[48] BLOOM B J, NICHOLSON T L, WILLIAMS J R, et al. An optical lattice clock with accuracy and stability at the 10-18level[J]. Nature, 2014, 506(7486): 71-75.

[49] BOADA O, CELI A, LATORRE J I, et al. Quantum simulation of an extra dimension[J]. Physical Review Letters, 2012, 108(13): 3001.

[50] CELI A, MASSIGNAN P, RUSECKAS J, et al. Synthetic gauge fields in synthetic dimensions[J]. Physical Review Letters, 2014, 112(4): 3001.

[51] ATALA M, AIDELSBURGER M, LOHSE M, et al. Observation of chiral currents with ultracold atoms in bosonic ladders[J]. Nature Physics, 2014(10): 588.

[52] PIRAUD M, HEIDRICH-MEISNER F, MCCULLOCH I P, et al. Vortex and Meissner phases of strongly interacting bosons on a two-leg ladder[J]. Physical Review B, 2015, 91(14): 406.

[53] NATU S S. Bosons with long-range interactions on two-leg ladders in artificial magnetic fields[J]. Physical Review A, 2015, 92(53): 623.

[54] AKATSUKA T, TAKAMOTO M, KATORI H. Three-dimensional optical lattice clock with bosonic88Sr atoms[J]. Physical Review A, 2010, 81(23): 402.

[55] CAMPBELL S L, HUTSON R B, MARTI G E, et al. A Fermi-degenerate three-dimensional optical layyice clock[J]. Science, 2017, 358(6359): 90-94.

[56] GEMELKE N, ZHANG X, HUNG C L, et al. In situ observation of incompressible mott-insulating domains in ultracold atomic gases[J]. Nature, 2009(460): 995-1002.

[57] BAKR W S, GILLEN J I, PENG A, et al. A quantum gas microscope for detecting single atoms in a Hubbard-regime optical lattice[J]. Nature, 2009(462): 74-80.

[58] SHERSON J F, WEITENBERG C, ENDRES M, et al. Single-atom-resolved fluorescence imaging of an atomic Mott insulator[J]. Nature, 2010, 467(7311): 68-72.

[59] STAMPER-KURN D M, UEDA M. Spinor Bose gases: symmetries, magnetism, and quantum dynamics[J]. Reviews of Modern Physics, 2013, 85(3): 1191.

[60] SADLER L E, HIGBIE J M, LESLIE S R, et al. Spontaneous symmetry breaking in a quenched ferromagnetic spinor Bose-Einstein condensate[J]. Nature, 2006, 443(7109): 312-316.

[61] ZHOU X, PAN J S, WEI Y, et al. Interaction-induced exotic vortex states in an optical lattice clock with spin-orbit coupling[J]. Physical Review A, 2017, 96(2): 3627.

[62] ZHANG R, CHENG Y, ZHAI H, et al. Orbital feshbach resonance in alkali-earth atoms[J]. Physical Review Letters, 2015, 115(13): 5301.

[63] PAGANO G, MANCINI M, CAPPELLINI G, et al. Strongly interacting gas of two-electron fermions at an orbital feshbach resonance[J]. Physical Review Letters, 2015, 115(26): 5301.

[64] HÖFER M, RIEGGER L, SCAZZA F, et al. Observation of an orbital interaction-induced feshbach resonance in173Yb[J]. Physical Review Letters, 2015, 115(26): 5302.

[65] BARBARINO S, TADDIA L, ROSSINI D, et al. Magnetic crystals and helical liquids in alkaline-earth fermionic gases[J]. Nature Communications, 2015(6): 8134.

[66] COOPER N R. Optical flux lattices for ultracold atomic gases[J]. Physical Review Letters, 2011, 106(17): 5301.

[67] GOLDMAN N, BUDICH J C, ZOLLER P. Topological quantum matter with ultracold gases in optical lattices[J]. Nature Physics, 2016(12): 639-645.

[68] CAZALILLA M A, REY A M. Ultracold fermi gases with emergent SU(N) symmetry[J]. Reports on Progress in Physics, 2014, 77(12): 4401.

[69] LI J R, LEE J, HUANG W J, et al. A stripe phase with supersolid properties in spin-orbit-coupled Bose-Einstein condensates[J]. Nature, 2017(543): 91-94.

[70] WANG C J, GAO C, JIAN C M, et al. Spin-orbit coupled spinor Bose-Einstein condensates[J]. Physical Review Letters, 2010, 105(16): 403.

[71] HO T L, ZHANG S. Bose-Einstein condensates with spin-orbit interaction[J]. Physical Review Letters, 2011, 107(15): 403.

[72] HAN W, ZHANG X F, SONG S W, et al. Double-quantum spin vortices in SU(3) spin-orbit-coupled Bose gases[J]. Physical Review A, 2016, 94(33): 629.

Brief introduction of spin-orbit coupling in optical lattice clock

WANG Lin-xue1,2,3, GUO Hui1,2,3, LIU Tao1,2,3, ZHANG Xiao-fei1,2,3

(1. National Time Service Center, Chinese Academy of Sciences, Xi’an 710600, China;2. Key Laboratory of Time and Frequency Primary Standards, Chinese Academy of Sciences, Xi’an 710600, China;3. School of Astronomy and Space Science, University of Chinese Academy of Sciences, Beijing 101048, China)

Based on the recent experimental realization of spin-orbit coupling in optical lattice clocks, we briefly introduce the experimental scheme for the generation of spin-orbit coupling. By comparing the optical-clock scheme and the traditional Raman scheme, we indicate the advantage of the former. We also discuss possible novel states of matter and quantum phenomena in the quantum degenerate regions, with emphasis on the important role played by the optical lattice clock in preparing, controlling and measuring new states of matter in ultra-cold atomic gases.

optical lattice clock; spin-orbit coupling; ultra-cold atomic gas; novel quantum state

10.13875/j.issn.1674-0637.2020-01-0001-08

2019-05-17；

2019-06-18

国家自然科学基金资助项目（11775253；11704383）

王林雪，女，博士，主要从事冷原子物理研究。