国家授时中心VLBI网13m射电望远镜指向修正

吴文雅，马浪明，姚当，刘佳，吴元伟，杨旭海,4

国家授时中心VLBI网13m射电望远镜指向修正

吴文雅1,2,3，马浪明1,2，姚当1,2，刘佳1,2，吴元伟1,2，杨旭海1,2,4

（1. 中国科学院 国家授时中心，西安 710600；2. 中国科学院 精密导航定位与定时技术重点实验室，西安 710600；3. 中国科学院大学 电子电气与通信工程学院，北京 100049；4. 中国科学院大学 天文与空间科学学院，北京 101048）

中国科学院国家授时中心根据VLBI2010技术规范要求研制的3台13 m射电望远镜，建成了我国第一套测地型VLBI（very long baseline interferometry）网，并进行实验观测。天线（射电望远镜接收信号的部分称之为天线）的指向精度直接影响到VLBI系统的观测性能，因此天线指向修正是VLBI网设施中最基础的工作。研究了影响13 m射电望远镜指向精度的物理根源，根据观测要求得出天线指向精度要求，并建立相对应的修正模型，根据13 m射电望远镜的情况，最终认定13m射电望远镜采用18参数的修正模型；研究了13 m射电望远镜实际测定的天线方向图及十字扫描法技术；分析、比较各种归算方法，采用傅里叶函数拟合方法确定其射电源精确位置；利用射电源高精度位置的优势，精确地测定13m射电望远镜各方向的指向误差，最后，用最小二乘法拟合得到18参数修正模型的系数值，实现了模型修正精度优于天线主瓣十分之一的目标，并对观测结果进行了验证。最终修正后指向精度为46.64"，优于天线主瓣十分之一（53.9"）的要求，达到VLBI系统观测要求。

VLBI网；射电望远镜；天线修正模型；最小二乘法

0 引言

甚长基线干涉测量（very long baseline interferometry，VLBI）是20世纪60年代后期发展起来的一种射电干涉技术，具有极高的角分辨率和测量精度，在天体物理、天体测量、大地测量和天文地球动力学等研究领域得到广泛的应用[1]。

中国科学院国家授时中心（NTSC）的3台13 m射电望远镜分别位于喀什、吉林、三亚，3台射电望远镜组成了我国第一套测地型VLBI观测网。国家授时中心的VLBI观测网天线参照国际VLBI2010规范，采用宽带技术，具备天线形变小、天线转动速度快和快速换源等特点，特别适用于航天器测定轨、地球定向参数（EOP）（特别是世界时UT1）连续测量、可有效支持时空基准的建立及相关地上物理学科的研究[2]。

天线组成的射电望远镜主体，是VLBI技术的基础，而天线的高精度的指向是对射电望远镜的基本要求，其精度不仅影响到望远镜观测目标源的能力，还会影响跟踪系统的观测效率。

NTSC 13 m射电望远镜采用稳定的地平式结构，自动化程序自动把目标源的赤道坐标转换为地平坐标，并直接控制天线软件ACU（antenna control unit，天线控制单元）进行自动化观测。13 m射电望远镜工作频率为1.2~9 GHz，频率越高天线主瓣宽度越窄，因此对指向的要求也越高，通常要求指向误差在十分之一波束宽度之内。天线主瓣波束宽度指天线功率方向图中半功率点的宽度HPBW（half power beam width）[3]为

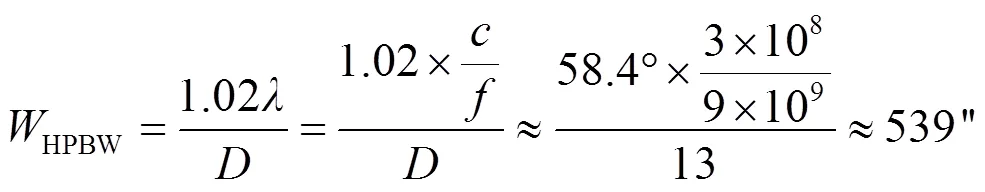
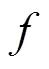
1 射电望远镜指向误差修正原理

射电源有相当高的位置精度，用以定义国际天球参考架，因此射电源可作为天线指向修正的实验目标，其理论位置与实际测量位置的偏差即为天线指向误差。天线建造时通过校准具备一定指向精度，但有些误差仍然无法通过校准完全消除，这类指向误差一般由多因素造成，可将这些误差分为系统误差和偶然误差两大类[4]。偶然误差是指天线指向误差无法用模型精确模拟的误差，如由温差引起天线热胀冷缩造成的偏差[5]，多变环境造成的偏差[6-7]，传动齿轮、齿隙的偏差等，这些无法模型化的误差不得不认作为“随机”特性的误差，选择合适的运行方式与合适的运行环境来尽量减小其“随机”误差的影响。系统误差可根据物理原因用模型精确模拟的误差，如电轴与机械轴不重合引起的误差、天线方位轴与天顶不重合引起的误差、编码器安装误差和天线重力形变误差等，这些误差对天线指向的影响具有固定的变化规律，建立误差修正模型并通过测量确定其影响，原则上可以消除这部分原因引起的误差。图1所示为天线指向误差修正原理图，根据影响天线指向的物理根源，分析天线指向每一个误差源的影响规律，将所有误差源的校正函数综合得到天线指向误差修正模型表达式，根据实际天线指向测定的结果，最后通过最小二乘法拟合求出模型的修正项参数值，得到最终的误差修正实际模型，并对天线指向修正进行验证，给出天线指向修正的精度。因此，本文重点讨论对系统误差的精确标定方法，并采用傅里叶级数修正项对偶然误差进行修正。

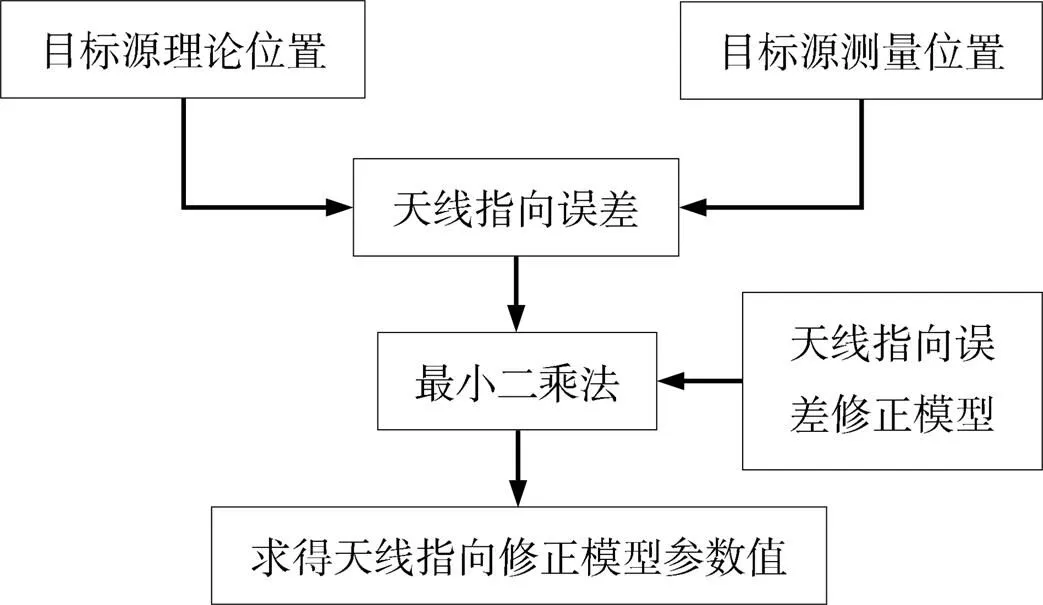
图1 天线指向误差修正原理图

1.1 指向误差源的分析

NTSC 13 m射电望远镜的指向误差源主要包括：天线电轴和机械轴不重合，俯仰轴与方位轴不正交，天线的天顶与真天顶不重合、编码器安装误差、天线重力变形误差等。分析这些误差对应的天线指向影响，给出影响天线指向的理论修正函数，最终得到完整的修正模型。

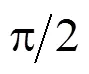
图2 地平坐标系

1.1.1 天线电轴和机械轴不重合的影响

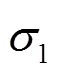
利用球面三角形第一五元素定律：

电轴与俯仰轴不正交最终改正为：

图3 电轴与机械轴不重合的影响

1.1.2 俯仰轴与方位轴不正交的影响

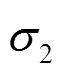
在三角形∆´中，有

式（6）中，影响为二阶小量，得出

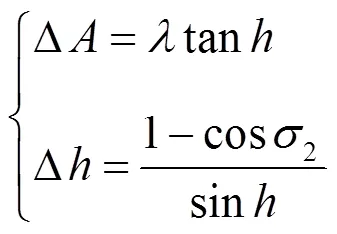
图4 俯仰轴与方位轴不正交

1.1.3 方位轴偏离天顶

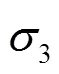
用正弦定律，得

即

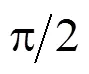
图5 方位轴倾斜

1.1.4 编码器误差

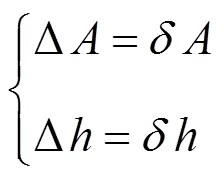
图6 方位轴码盘偏心误差影响

1.1.5 天线重力变形误差

由于重力作用，天线会产生形变，在仰角为0°时，影响最大，由于对称性及重力对天线形变影响，仅对仰角引起误差，改正值可表示为

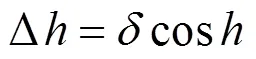
1.2 建立指向模型

通过以上初步分析，我们可以得到主要的几个误差修正项。修正项通过分析过程可以得到，实际误差并非完全符合总结的规律，而且还有一些随机变化的影响因素，这些因素引起的误差通过以上修正项无法完全消除，所以在以上的基础上还需进一步寻找经验项建立新模型。

1.2.1 几种常见的射电望远镜指向误差修正模型

① 射电望远镜8参数修正模型为：

表1 射电望远镜8参数指向误差修正模型参数含义对照表

上海天文台模型与云南天文台模型，包括新西兰模型均采用8参数修正模型，只是书写方式略有差异，但其代表的物理意义均相同。

② 佳木斯66 m射电望远镜12参数修正模型为：

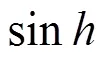
1.2.2 NTSC 13 m射电望远镜18参数指向误差修正模型

8参数误差修正模型基本消除了大部分物理原因引起的误差，12参数误差修正模型考虑天线不对称影响，但是仍然无法消除模型近似带来的误差。本文提出加入傅里叶级数修正项的修正模型，得到18参数新模型：

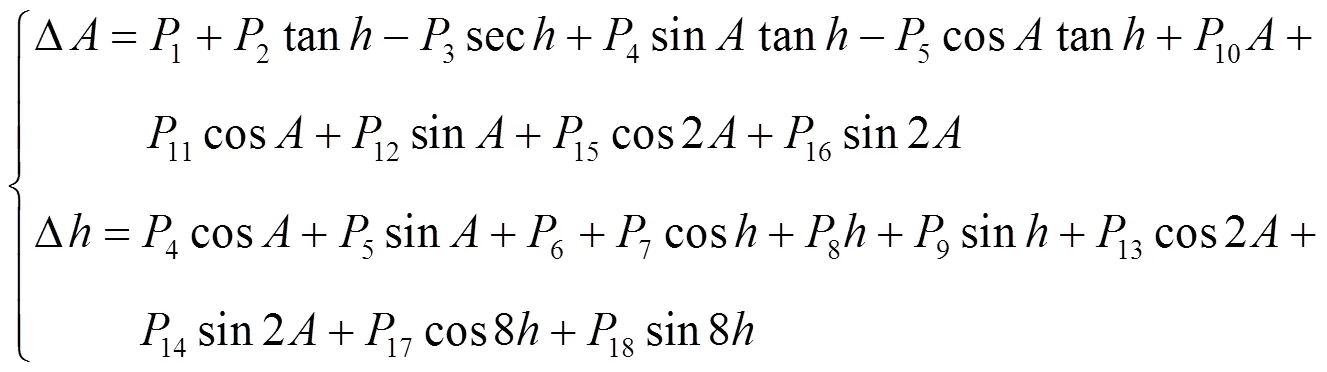
式（17）中各项系数对应含义示于表2。

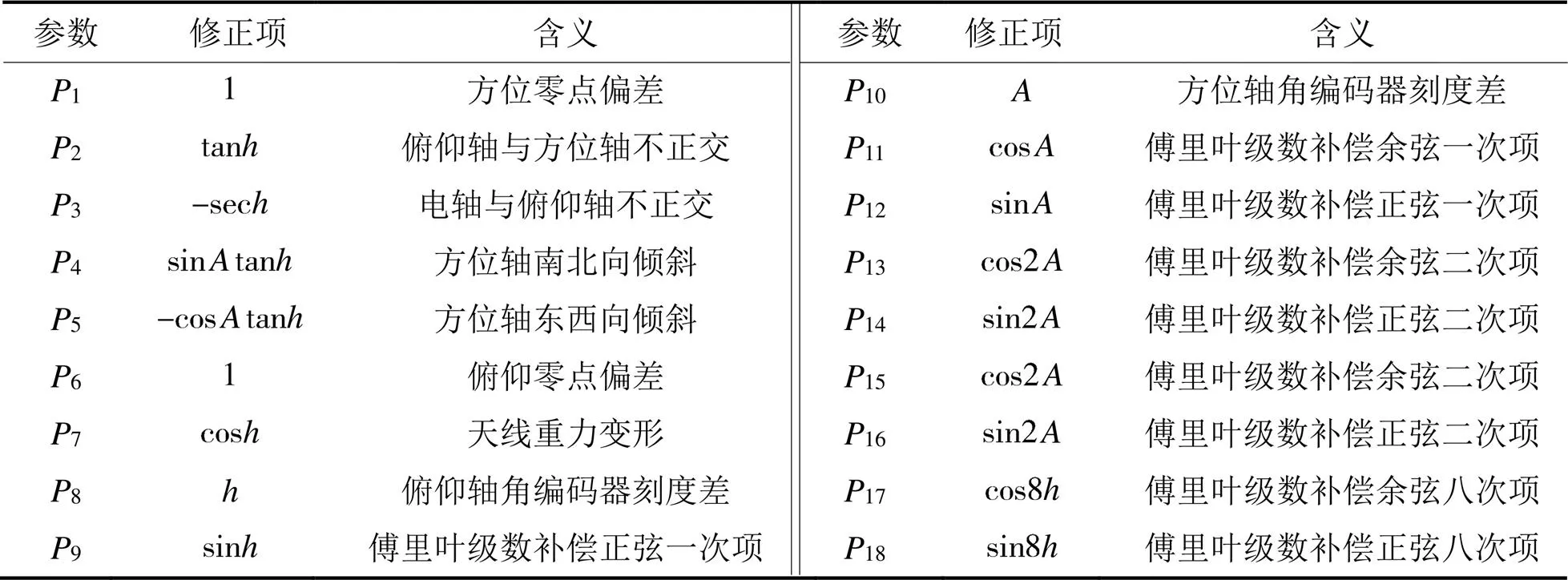
表2 NTSC 13 m射电望远镜指向误差修正模型参数含义对照表

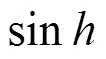
图7 函数曲线图

随着模型参数增多，模型对最终拟合所用的数据依赖性更强，受观测点在天区分布情况的影响更大，因此观测时应选择能较好分布全天区的目标，并且不应再增加过多修正项，以防模型过度拟合，影响精度。18参数模型可更好地消除未知因素和模型近似带来的误差，适用于天线转速快、形变小的13 m射电望远镜；因12参数模型可更好消除重力变形和方位轴与俯仰轴不正交等影响的特点，适用于重量大、地基变形的射电望远镜；对于更小型射电望远镜可采用方便拟合的8参数模型。

2 射电望远镜指向误差确定

国家授时中心的3台13 m射电望远镜结构功能基本相同，指向修正模型相似，本文仅对三亚台站13 m射电望远镜进行研究。

2.1 天线功率方向图与十字扫描法

射电望远镜在不同方向上接收信号的能力通常用天线功率方向图来描述[12]，如图8和9所示为理论天线功率方向图和实测天线功率方位图。由图可知当天线指向功率方向图主瓣方向时，接收信号最强，天线偏离目标源时信号会有很大强度的降低。根据此特性，可先引导天线对准目标源，对天线方位角度和俯仰角度进行正向与负向偏置扫描，以此得到偏置方向的功率值，从而画出实测天线功率方向图。此扫描方法先后进行方位和俯仰的扫描，天线在天空中扫描到的位置形如一个“十”字，称之为十字扫描法。

图8 理论天线功率方向图

图9 实测天线功率方位图

2.2 目标源测量位置

十字扫描的目的是为了得出功率方向图中主瓣波峰位置，此位置即为该时刻目标源实际测量位置，显然此位置为功率最大点，由于信号存在干扰，可能最高点位置并非目标源实测位置，如图10所示为有干扰的十字扫描功率点。因此不能简单地通过找最大点来确定实际指向位置。

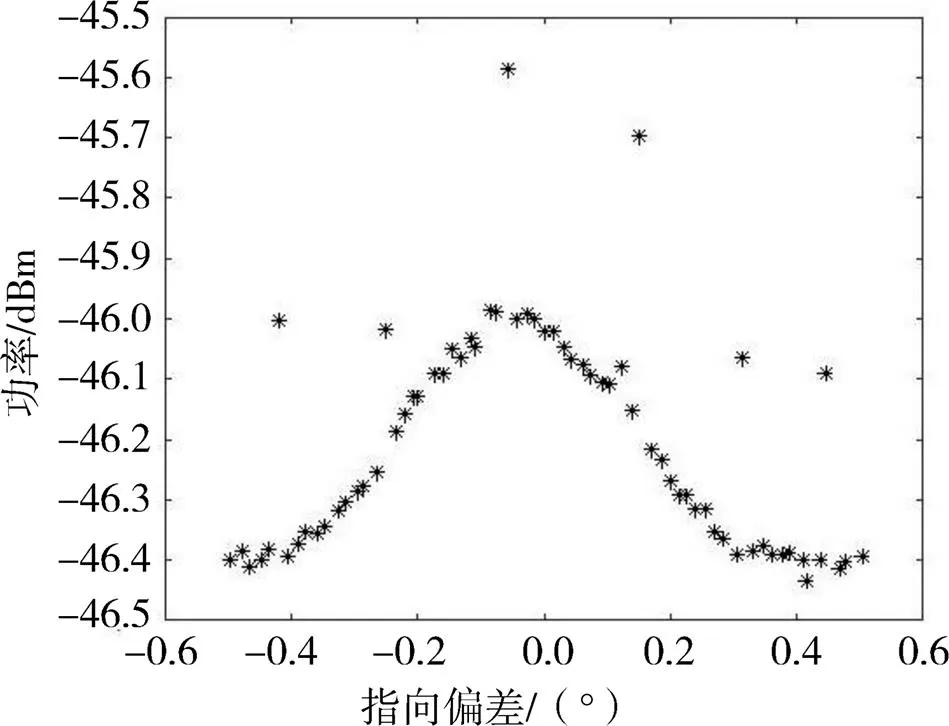
图10 有干扰的十字扫描功率点

通过观察天线方向图和十字扫描后采集的数据点图，如图8、11、12、13所示，发现功率曲线波形同高斯函数波形、傅里叶函数波形等很相似。将功率点进行曲线拟合，通过拟合的曲线得到最大点，此最大点最接近于实测位置。

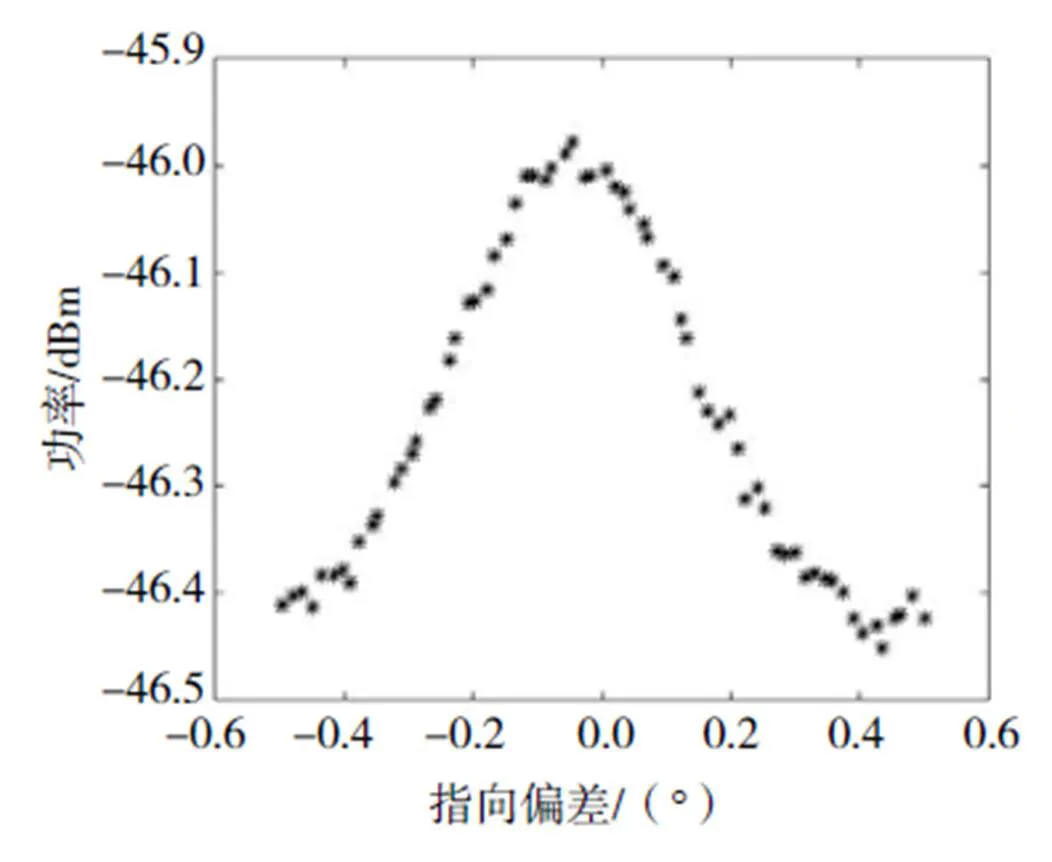
图11 无干扰的十字扫描功率点

图12 高斯函数波形

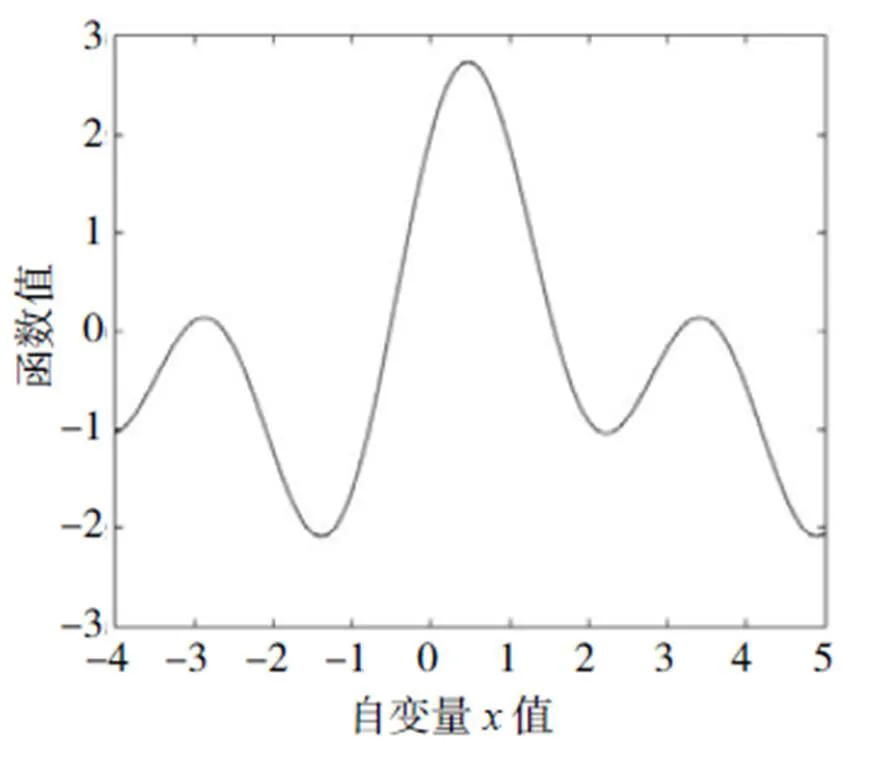
图13 傅里叶函数波形

首先尝试高斯函数拟合，高斯函数公式如下

在用高斯函数实现拟合的过程中发现结果并不理想，于是采用参考文献[13]中方法，在高斯函数后加入三次项进行拟合，函数式见式（19），拟合后功率图如图14所示，功率图横坐标为方位差或俯仰差，纵坐标为功率大小。

由图14可看出加入三次项后的高斯拟合效果仍然很差，所以尝试傅里叶函数拟合，式（20）为拟合公式，拟合后功率图如图15所示，比较图14和图15可看出傅里叶拟合效果更好，因此本文将采用傅里叶拟合确定目标源实际测量位置。

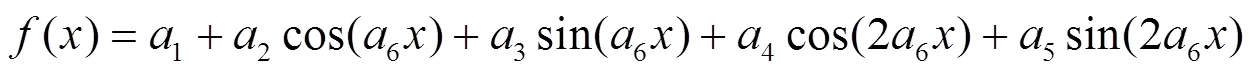
图14 加入三次项后的高斯拟合功率图

图15 傅里叶拟合功率图

3 指向模型拟合及实测结果

根据强标准射电源稳定易跟踪的特性，实验选择强标准射电源作为实验目标源[14]。考虑到所选射电源位置周边不能有强的射电背景影响定位，另外所选源的方位、俯仰能较好的全天区覆盖，所以最终本实验选择3C144，3C274，3C405，3C461和3C279等共13个强射电源作为目标源进行观测。天区覆盖如图16所示。

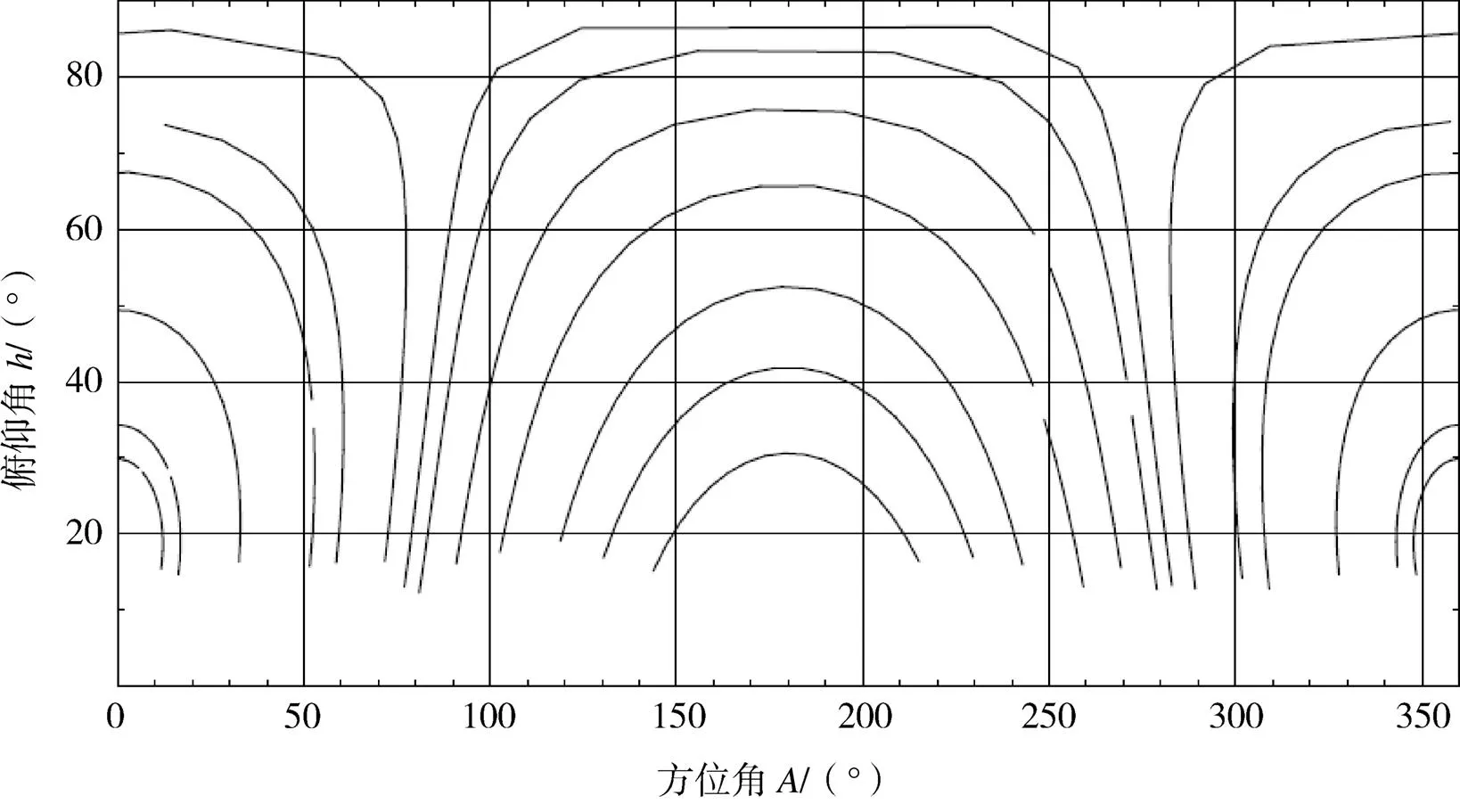
图16 目标射电源轨迹分布图

指向十字扫描波形特征明显，如图11所示，根据扫描波形易判断信号是否存在异常或干扰，出现异常或严重干扰时因更换目标源或剔除该段数据，出现如图10所示轻微干扰时，可通过剔除异常数据点的方法消除干扰。

3.1 指向模型最小二乘拟合

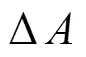
表3 NTSC三亚站13 m射电望远镜指向误差修正模型参数值

3.2 指向误差修正精度

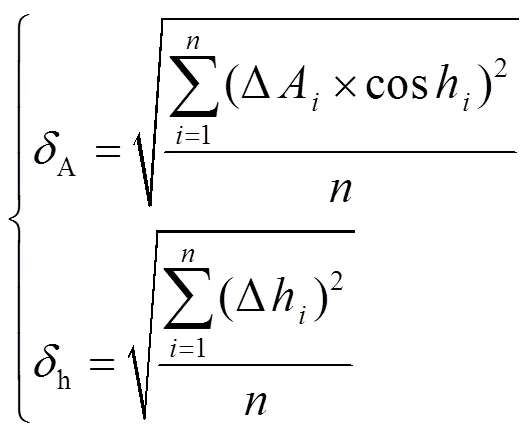
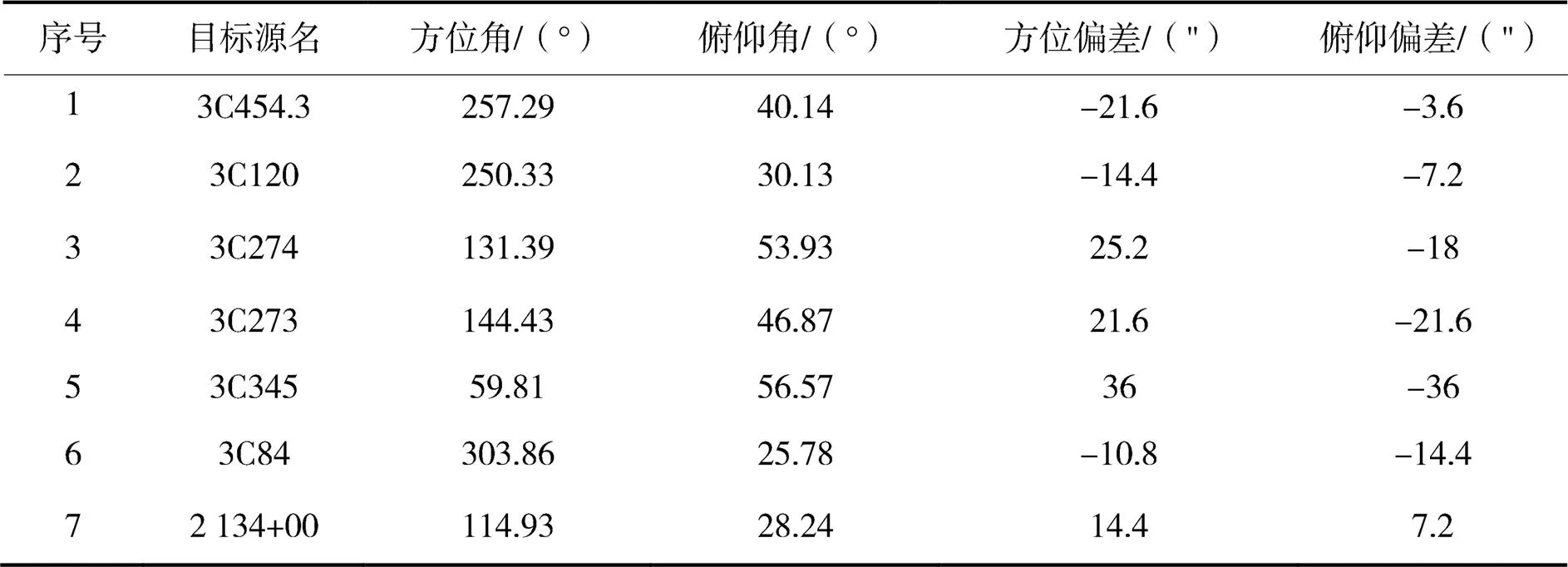
表4 NTSC 13 m射电望远镜指向误差验证数据

续表4

4 结语

本文从射电望远镜指向误差源入手，对不同误差源进行分项修正，并加入傅里叶级数项来消除部分未知误差，相比其他误差修正模型更为精确。本次实验一共进行610次实际观测，获得NTSC 13 m射电望远镜方位指向误差32.25"，俯仰指向误差33.69"，总指向误差46.64"，满足预定的53.9"指向精度要求。需要注意的是，由于射电望远镜的指向误差会跟随时间的推移而变化，需要在半年时间左右重新校准一次。

[1] 钱志瀚, 李金岭. 甚长基线干涉测量技术在深空探测中的应用[M]. 北京: 中国科学技术出版社, 2012.

[2] 姚当, 弓剑军, 马浪明, 等. 基于VGOS系统的UT1初步观测与计算[J]. 时间频率学报, 2018, 41(3): 234-241.

[3] ROHLFS K, WILSON T L. 射电天文工具[M]. 北京: 北京师范大学, 2008.

[4] 赵彦. 大射电望远镜指向误差建模分析与设计研究[D]. 西安: 西安电子科技大学, 2008.

[5] UKITA N. Thermal effects on the pointing of the Nobeyama 45-m telescope[J]. Publication of the Astronomical Society of Japan, 1998, 4(1): 1-5.

[6] SMITH D R, TIMOTHY P A, AMY L J, et al. Measurements of dynamic pointing variations of a large radio telescope[J]. SPIE, 2000, 4015: 467-475.

[7] HU K Y, YUSUP A L, XU Q. Deformation measurement and pointing model analysis of 25 m antenna[J]. Applied Mechanics and Materials, 2015, 3744(713): 424-431.

[8] GUIAR C N, LANSING F L, RIGGS R. Antenna pointing systematic error model derivations[J]. Telecommunications & Data Acquisition Progress Report, 1987, 88: 36-46.

[9] MEEKS M L, BALL J A, HULL A B. The pointing calibration of the Haystack antenna[J]. IEEE Transactions on Antennas & Propagation, 1968, 16(6): 746-751.

[10] LEWIS H, LUPTON W, SIROTA M J, et al. Pointing and tracking performance of the W.M. Keck Telescope[C] // SPIE 1994 Symposium on Astronomical Telescopes & Instrumentation for the 21st Century: Advanced Technology Optical Telescopes V, Kailua, Kona, HI, United States: 1994: 117-125.

[11] 喻业钊, 韩雷, 周爽, 等. 佳木斯66 m射电望远镜指向精度测量及改进[J]. 天文研究与技术, 2016, 13(4): 408-415.

[12] 克里斯琴森W A, 霍格玻姆J A. 射电望远镜[M]. 陈建生, 译. 北京: 科学出版社, 1977.

[13] 虞林峰, 王锦清, 赵融冰, 等.TM65 m射电望远镜指向模型的建立[J]. 天文学报, 2015, 56(2): 165-177.

[14] 高冠男, 汪敏, 施硕彪, 等. 云台40 m射电望远镜的指向误差校正[J]. 天文研究与技术, 2007, 4(2): 188-194.

[15] 刘卫国.MATLAB程序设计教程[M]. 北京: 中国水利水电出版社, 2010.

Pointing calibration of 13 m antenna of VLBI network at National Time Service Center

WU Wen-ya1, 2, 3, MA Lang-ming1, 2, YAO Dang1, 2, LIU Jia1, 2, WU Yuan-wei1, 2, YANG Xu-hai1, 2, 4

2. National Time Service Center, Chinese Academy of Sciences, Xi’an 710600, China; Key Laboratory of Precise Positioning and Timing Technology, Chinese Academic of Sciences, Xi’an 710600, China;School of Electronic, Electrical and Communication Engineering, University of Chinese Academy of Sciences, Beijing 100049, China；School of Astronomy and Space Science, University of Chinese Academy of Sciences, Beijing 101048, China)

The first wide band domestic geodetic VLBI (very long baseline interferometry) networks, developed by the National Time Service Center (NTSC) of the Chinese Academy of Sciences, that is composed of three 13-meter radio telescopes and is now on commissioning phase. The pointing accuracy of the antenna is directly affecting the observation performance of the VLBI system, so, the antenna pointing correction is of one of the most basic works of the system. In this thesis, the error sources of the antenna pointing are studied. In order to meet the requirements of astronomical observations, a pointing correction model is established. The antenna pattern is measured by cross-scan method. And a 18-parameter correction model is established. By analyzing and comparing various reduce methods, we adopt the Fourier function fitting method to determine the precise position of radio sources, then, measured antenna errors for all directions. Finally, the coefficient values of the 18-parameter correction model are obtained by least squares fitting method. The final corrected accuracy is 46.64", which is better than the one-tenth (53.9") of the main lobe of the antenna, thus meets the requirements of astronomical observations.

very long baseline interferometry (VLBI) network; radio telescope; pointing model; least square method

10.13875/j.issn.1674-0637.2020-01-0041-13

2019-05-17；

2019-06-18

国家自然科学基金面上资助项目（11173026）；中国科学院国家授时中心青年创新人才资助项目；载人航天预研资助项目（0602）

吴文雅，男，硕士，主要从事VLBI及射电望远镜指向方面的研究。