一类具有时滞的比例依赖型捕食者-食饵模型的稳定性
崔舒为, 张 婧
(兰州交通大学 数理学院, 甘肃 兰州 730070)
0 引言
探究捕食者种群与食饵种群之间的动态关系是种群生态学体系的重要主题之一.自第一个预测捕食者种群及其资源种群数量变化的数学模型即Lotka-Volterra模型[1]出现之后, 捕食者-食饵模型就成为了学者们关注与研究的对象. 近年来对于捕食者-食饵模型的研究更是层出不穷. 如:付静研究了在白噪声扰动下具有比例依赖的捕食者-食饵模型的动力学性质[2]; 邵长旭从分形理论的角度讨论了三种群的捕食者-食饵模型[3]; 朱子睿等对捕食者-食饵模型增加了扰动扩散项, 分析了其平衡解的全局渐近稳定性[4]. 随着研究的不断深入与拓展, 时间因素对种群密度的影响逐渐成为研究的焦点. 目前对这类方程的研究主要集中在平衡点存在性、稳定性和周期解等方面.
2012年,Banerjee M[5]研究了如下捕食者-食饵模型

(1)

2005年,周淑荣[10]等研究了具有Allee效应的捕食者-食饵模型正平衡点的稳定性. 2009年,Celik[11]对此模型中的食饵种群引入了时滞, 探究了模型正平衡点的局部渐近稳定性和Hopf 分支问题.
受文[5][10][11]启发, 考虑由于食饵种群妊娠期产生的时间滞后对模型(1)产生的影响, 对模型(1)中的食饵种群引入时滞, 得到如下模型

(2)
1 局部稳定性与Hopf 分支
1.1 平衡点的存在性,解方程组
可得模型(2)的平衡点
定理1 若
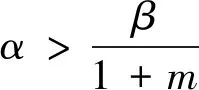
(3)
成立, 则模型(2)存在唯一正平衡点E*(u*,v*).
1.2 平衡点的稳定性
令x(t)=u(t)-u*,y(t)=v(t)-v*,得到(2)的线性化系统
即

(4)
其对应的特征方程为:
即

(5)
令
则式(5)化为:
λ2+Pλ+Q+Re-λτ=0
(6)
1.2.1τ=0时正平衡点的稳定性
当不考虑时滞,即τ=0时,式(6)可表达为λ2+Pλ+Q+R=0,容易得出: 当P>0,Q+R>0时, 即

(7)
时,系统平衡点E*渐近稳定.

1.2.2τ≠0时正平衡点的稳定性
令λ=iω(ω>0)为方程(6)的一个根, 把iω(ω>0)代入方程(6), 得
(iω)2+Piω+Q+R(cosωτ-isinωτ)=0.
分离上述方程的实部与虚部,得

(8)
把上述方程的两端平方相加, 得到关于ω的代数方程
ω4+(P2-2Q)ω2+Q2-R2=0
(9)
当P2>2Q,Q2>R2时,对于任意的τ>0,方程(9)的所有根都具有负实部,系统平衡点E*局部渐近稳定.
当Q2 当P2<2Q,Q2>R2时,方程(9)存在两个正根 对方程(6)求关于τ的导数, 得: 得到横截性条件 定理3 对于系统(2), 假设(3)成立. 1) 若P2>2Q,Q2>R2, 即 (10) 成立, 则对于所有τ>0, 系统(2)的平衡点E*局部渐近稳定. 2) 若Q2 (α(1+m)2-β(2+m))2<β2 (11) 成立, 则当τ<τj时, 系统(2)的平衡点E*是渐近稳定的; 当τ>τj时, 平衡点E*不稳定,当τ=τj时, 系统(2)在平衡点E*处发生Hopf 分支. 3) 若P2<2Q,Q2>R2, 即 (12) 图1 当τ取3时模型(2)平衡点的稳定情况 例2 在模型(2)中令α=3,β=3,m=0.5, 则模型(2)存在唯一正平衡点E*(1,1), 这些系数满足(3)和(11), 当τ>0时, 根据上节计算可得ω+=0.899,τj=0.604. 图2说明当τ<τj时, 平衡点E*(1,1)渐近稳定; 图3说明当τ在τj附近时一个稳定的周期解从平衡点E*(1,1)分支出来. 图2 当τ取0.45时模型(2)平衡点的稳定情况 图3 当τ取0.6时模型(2)平衡点的稳定情况 研究了一类具有时滞的比例依赖型捕食-食饵模型. 考虑了食饵种群妊娠期对捕食者-食饵模型种群密度带来的时间滞后影响. 当模型(2)存在唯一正平衡点即式(3)成立时, 若模型(2)中的系数满足条件(3), 时滞不会影响模型正平衡点的稳定性; 若模型(2)中的系数满足条件(11)或条件(12), 当时滞达到某个临界值时会影响模型正平衡点的稳定性并导致分支的出现.

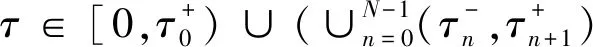
2 数值模拟




3 结论

