基于有序FP-tree结构和投影数据库的最大频繁模式挖掘算法
王利军, 唐 立
(安徽经济管理学院 信息工程系, 安徽 合肥 230031)
0 引言
关联规则是数据挖掘的重要研究领域,挖掘频繁模式是关联规则中的重要内容.1993年,Agrawal等人提出了挖掘频繁模式的Apriori算法[1];2000年,Han等人提出了FP-growth算法[2],该算法是基于FP-tree树结构的挖掘算法[2].挖掘频繁模式会产生大量的频繁模式,随着事务数据库的增大和支持度阈值设置的较小时,频繁模式的规模会更大.
在实际应用中,最大频繁模式在某些领域更具有价值,并且最大频繁模式包含了所有的频繁模式信息,因此许多专家学者对最大频繁模式的挖掘进行了深入的研究,具有代表性的最大频繁模式挖掘算法有MaxMiner[3]、MAFIA[4]、FP-Max[5]等.这些算法仍然存在改进的空间,比如,FP-Max是基于FP-tree树结构的挖掘算法,树结构会长期占用较大的系统资源,算法采用递归调用的方式挖掘数据,执行效率低下,因此尽量减少系统资源的的消耗和减少递归调用的次数成为加快FP-Max算法的执行效率的首要问题.本文将采用有序FP-tree替代FP-tree减少系统资源的浪费,并在此基础上,采用垂直投影方案生成投影数据库,基于投影数据库创建局部FP-tree从而进一步减少空间资源的浪费,并且采用相应的策略减少没必要的挖掘过程,最终达到提高挖掘效率的目的.
1 问题描述和改进策略
1.1 问题描述
FP-Max算法目前存在的问题如下:
1) FP-tree树结构的每一个节点(除根节点外)都包含6个域,分别存放节点名、支持度计数、孩子节点的指针、父节点的指针、兄弟节点的指针、同名节点的指针.基于事务数据库创建的初始FP-tree树结构在整个挖掘过程中一直存在,这样将长期占据系统空间资源.
2) FP-Max算法采用递归的挖掘方式,期间会产生大量的条件子树,这些条件子树也是基于FP-tree树结构的,这样并会加大对系统空间资源的消耗.若事务数据库规模庞大或者支持度阈值较小时,这种情况会更严重,可能会导致内存溢出而无法正常挖掘.
3) 项头表中的每个事务项都需要被挖掘,这样会大大降低挖掘效率.系统资源的长期占用,以及递归挖掘方式和创建条件子树都会影响算法的整体执行效率.
1.2 改进策略
针对上述3个问题,论文提出以下改进策略:
策略1: 采用有序FP-Tree[6]代替FP-Tree,从而减少对系统空间资源的浪费;
策略2: 引入“分而治之”的思想,分解事务数据库得到投影数据库,基于投影数据库[3]创建局部树结构,从而进一步减少对系统空间资源的浪费;
策略3: 利用有序FP-Tree树结构的性质减少挖掘次数;
策略4: 采用优化方案减少投影次数加快挖掘效率;
本文在改进策略的基础上提出了基于有序FP-Tree和投影数据库的挖掘最大频繁模式算法OPFP-MAX算法.
2 实现改进策略
2.1 有序FP-tree替代FP-tree
有序FP-tree树结构的项头表包含3个域,别为ItemName、ID和FirstLink.ItemName域存放事务项的名称,按照支持度计数的大小降序排列;ID域存放编号,从1开始依次递增1升序排列,事务项名称与编号一一对应,方便后期生成最大频繁模式后进行转换;FirstLink域指向第一个相应事务项节点的位置.
有序FP-tree中的的每个节点只包含4个域空间,分别为NodeName,NodeCount,hLink,vLink.NodeName域存放节点的事务项名称;NodeCount域存放节点的支持度计数;hLink域在建立树结构时指向兄弟节点,建树完成后指向相同NodeName的下一个节点位置,vLink域在建立树结构时指向第一个孩子节点,建树完成后实现逆转指向父节点.有序FP-tree的建立过程中,同一个父节点的子节点在插入时需要按照编号的大小升序依次排列,这样的排列结构可以为建树过程中减少遍历子节点的个数,提高了建树的效率.有序FP-tree的每个节点只包含4个域空间,占用的内存空间约为FP-tree的2/3.有序FP-tree是单向的,有序FP-tree中只存在指向父节点的垂直指针和指向相同编号的水平指针.建树过程可以利用水平方向上的有序性减少遍历子节点的个数,加快建树效率,有序FP-tree的垂直方向上的有序性可以为后期挖掘最大频繁项集时减少事务项的挖掘数量,加快挖掘效率.
2.2 引入“分而治之”的思想
FP-Max算法需要将事务数据库的信息一次性装载到FP-tree树结构形成初始FP-tree树结构,如果事务数据库较大,可能会因内存溢出而无法进行装载,倘若可以一次性装载成功,这样势必会长期占用较大的系统空间资源,即使已经使用有序FP-tree替代FP-tree,但仍然是一笔不小的开销.为了解决这一问题,我们引入了“分而治之”的思想,它是将事务数据库采用某种方案进行分解形成一系列较小的数据库,我们称这些较小的数据库为投影数据库,然后基于投影数据库再形成的局部FP-tree[7],若有必要可递归投影并挖掘.
最大频繁模式存放在MFS集合中,若频繁1-项集的事务编号列表为1、2、3、4、5,令MFS|1为以事务编号1为结尾的最大频繁模式的集合,以此类推,则MFS=MFS|1∪MFS|2∪MFS|3MFS|4∪MFS|5,挖掘最大频繁模式可以转换成挖掘以这些事务编号为结尾的最大频繁模式,因此可以采用分治策略.
事务数据库的分解方案很多,比如并行投影方案[8]和垂直投影方案[9]等.使用不同的分解方案得到的投影数据库的事务内容也不尽相同,本文采用的分解方案为垂直投影方案.
在采用垂直投影方案之前需对事务数据库D进行如下处理:第一次扫描事务数据库D得到全局项头表L{x1,x2,…,xn-1,xn},项头表中采用降序的方式存放频繁1-项集,L的事务项总数为n,x1为支持度计数最高的事务项,xn为支持度计数最低的事务项,删除事务数据库D的每个事务中的非频繁项,并将每个事务中的事务项按照L中支持度计数降序排序.这样得到预处理事务数据库D1.
定义1 垂直投影方案 首先根据L的事务项总数n创建一个堆栈组Z{x1,x2,…,xn-1,xn},根据D1中的事务的最后事务项进行分组,将以x1为最后事务项的事务去除x1后分配到堆栈x1中,以此类推,这样既可得到初始投影数据库,然后从堆栈xn开始获取投影数据库信息构建局部FP-tree,并进行挖掘若有必要可递归挖掘得到局部模式,挖掘完成后将堆栈zn中每一个事务,继续采用垂直投影到其他堆栈(除堆栈zn),接着基于堆栈zn-1中投影数据库构建局部FP-tree继续挖掘,挖掘完成后将堆栈zn-1中每一个事务,继续采用垂直投影到其他堆栈(除堆栈zn和zn-1),采用相同的方式直到堆栈z1的投影数据库也被挖掘,算法执行完毕,合并所有的局部频繁模式.
2.3 减少挖掘策略可以减少挖掘的事务编号个数
有序FP-tree的事务项编号为1,2,3,…,n,根据有序FP-tree树结构的特点,该树结构具有如下特性.
定义2 若从根节点向下查找,从事务编号1开始找到连续的事务编号直至k所组成的路径<1,2,3,…,k>(k≤n),k的支持度计数大于等于最小支持度minsup,k不存在后续节点或后续节点支持度计数小于minsup,则<1,2,3,…,k>组成路径必为最左最大分支,该路径所形成的项集{1,2,3,…,k}必为频繁项集.根据频繁项集的任何真子集都不可能是最大频繁项集,因此{1,2,3,…,k-1}的任何子集都不是最大频繁项集.
减少挖掘策略:若找到最左最大分支<1,2,3,…,k>(k≤n),则在挖掘最大频繁项集时,只需要从项头表的最后一项n开始挖掘,直至事务项编号k,而事务项编号1,2,3,…,k-1都无需挖掘,从而达到减少挖掘的事务项个数,加快挖掘效率的目的.
2.4 采用优化方案减少投影次数加快挖掘效率
在减少挖掘策略的基础上,我们可以继续采用优化方案来加快挖掘效率,具体描述如下:在挖掘项头表中事务编号w(k≤w≤n)得到的候选最大频繁项集,若该候选最大频繁项集不是MFS的子集,则存入最大频繁项集集合.立即形成项集{1,2,3,…,w-1},检测该项集是否是最大频繁项集集合中某一个项集的子集,如果是,则挖掘算法可以终止,因为随后挖掘肯定不会得到新的最大频繁项集,因此无需再投影和挖掘,从而达到减少投影次数加快挖掘效率的目的.
3 举例
3.1 生成初始投影数据库
设置最小支持度计数为2,扫描事务数据库D删除每个事务中非频繁项并采用降序排序,进行编号得到预处理事务数据库D1如表1所示:

表1 预处理事务数据库D1
采用垂直投影方案对D1中的编号列表进行操作生成初始投影数据库,堆栈6中的项目包含了所有事务编号6的事务,其他堆栈暂时不完整.堆栈中的项目的演变过程如表2所示.
3.2 创建局部FP-tree树进行挖掘
基于堆栈创建局部FP-tree树后,首先获取最左最大分支,若符合要求可采用减少挖掘策略减少挖掘的事务编号个数,从而加快挖掘效率.
堆栈6中保存的项目是事务编号6的条件模式基,因为所有以事务编号6为结尾的事务经过处理后都保存在堆栈6中了.基于堆栈6创建事务编号6的条件FP-tree树FP-tree|6,该树只包含单路径<2,3,4:2>,故直接获得候选最大频繁模式{2,3,4,6:2},此时的MFS为空,{2,3,4,6:2}直接加入MFS.将堆栈6的项目继续采用垂直投影方案继续投影,使得堆栈4中增加了<1,2,3>和<2,3>两个项目,此时可以删除堆栈6减少空间的浪费.
开始对堆栈5进行挖掘,构建局部FP-tree树FP-tree|5,该树只包含单路径<1:2>,故可以直接获得候选最大频繁模式{1,5:2},检测MFS后,加入MFS.将堆栈5的项目继续采用垂直投影方案继续投影后,删除堆栈5.
挖掘堆栈4,生成局部FP-tree树FP-tree|4,该树不是单路径,需要递归挖掘,发现事务编号3的条件模式基为{1,2:1}和{2:1},直接生成局部FP-tree树FP-tree|3-4为单路径,获得候选最大频繁模式{2,3,4:2},该项集为MFS中{2,3,4,6:2}的子集故舍弃,同理获得事务编号2和1的最大频繁模式分别为{2,4:2}和{1,4:2},因{2,4:2}是MFS的子集故舍弃,{1,4:2}符合要求加入MFS,堆栈4挖掘完毕.继续投影后删除堆栈4.
同理挖掘堆栈3获得候选最大频繁模式{1,2,3:2},检测后可加入MFS.
至此算法结束,根据优化策略发现项集{1,2}是MFS中{1,2,3:2}的子集,故堆栈1和堆栈2不用再继续投影挖掘.
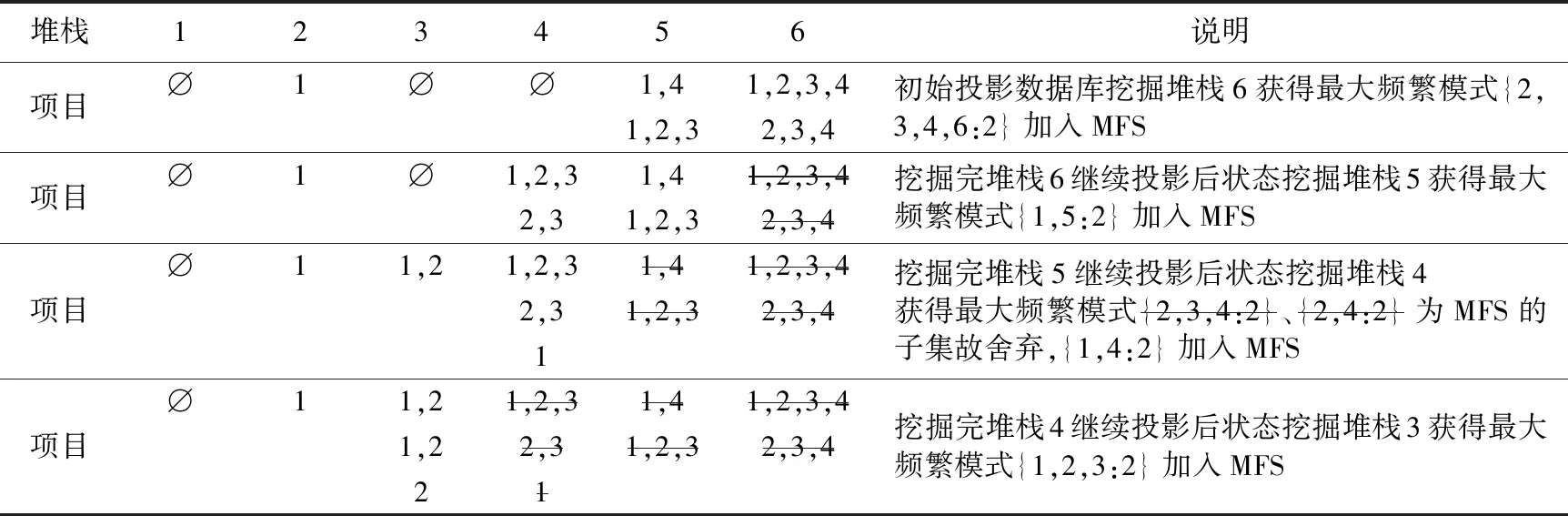
表2 投影数据库演变过程
最终,MFS中的最大频繁模式为{2,3,4,6:2}、{1,5:2}、{1,4:2}和{1,2,3:2}.
4 算法性能测试
采用OPFP-MAX和FP-Max两种不同的算法对相同数据库集进行挖掘比较,通过图表的方式显示挖掘的时间效率和空间使用情况,分析图表验证OPFP-MAX算法的优越性.

表3 数据集信息
OPFP-MAX和FP-Max两种不同的算法在两种数据集上的执行时间和内存消耗情况分别如图1和图2所示,OPFP-MAX算法在两种类型的数据集上都具有较好的执行效率,并且内存消耗上也相对较少,因此OPFP-MAX算法比FP-Max更加优越.

a.Retail数据集执行时间比较图 b.Pumsb数据集执行时间比较图图1 执行时间比较图
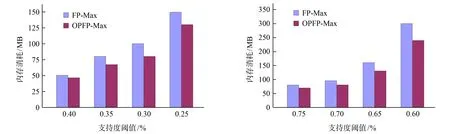
a.Retail数据集内存消耗比较图 b.Pumsb数据集内存消耗比较图图2 内存消耗比较图
5 结论
本文提出的基于有序FP-tree结构和投影数据库的最大频繁项集挖掘算法OPFP-MAX,该算法不仅可以减少空间资源的浪费,还利用有序FP-tree的特点加快建树效率且减少了挖掘事务编号的个数,再结合优化策略减少投影次数,最终达到加快挖掘效率的目的.但算法还是基于FP-tree树结构的,并且仍采用递归方式进行挖掘的,下一步的工作是直接通过事务数据库在不创建FP-tree树结构的基础上采用相应的方案获得最大频繁模式.

