多元线性分析在储粮真菌生长预测中应用研究

王鹏杰 祁智慧 张海洋 田 琳 高瑀珑 唐 芳

(国家粮食和物资储备局科学研究院1，北京 100037)

(南京财经大学2，南京 210023)

稻谷储藏期间，霉变是造成储粮损失的一个重要因素。近几十年来，国内外有关稻谷储藏霉变的研究报道很多。Laca等[1]研究发现霉菌主要分布在稻谷表面。Genkawa等[2]研究了不同水分的稻谷储藏过程中霉菌数量的变化，低水分稻谷无霉菌生长，其储藏的效果同低温储藏一样有效。周建新等[3-5]研究了不同贮藏条件下稻谷真菌的变化情况，环境温度和稻谷含水量对稻谷储粮真菌生长有直接影响，储藏温度和时间与霉菌量呈显著的二元线性关系。金昌福[6]等利用近红外检测技术，建立了贮藏环境温度和水分含量对贮藏稻谷表面霉菌菌落总数影响规律的多元线性回归模型。唐芳等[7]通过对稻谷储藏过程中水分和温度的变化与真菌生长关系的研究，得出稻谷储存水分、温度与真菌起始生长时间的关系曲线。上述研究都是侧重于一个或两个因素的影响，而真菌生长是受多个因素的影响，且相互耦合共同对真菌生长产生影响，因此，要更真实地反映真菌生长状况，需基于大量数据进行统计分析，建立多影响因素的真菌生长预测模型。

多元线性回归是多元统计分析中一种重要方法，可以解决多个因素对同一变量影响的相关性分析，进而建立相关性的统计模型。Green等[8]基于室内温度、湿度等变量建立了室内有害微生物的多元线性回归预测模型，预测模型精度可达97%。南英华等[9]建立了泉流量与大气降水的多元线性回归模型。本文基于水分、温度和储藏时间三个主要影响因素，定期采集真菌生长数据，采用多元线性回归建立储粮真菌生长预测模型，并对模型进行了F检验、t检验和残差分析，结合稻谷实仓数据对预测模型进行了初步验证。

1 材料与方法

1.1 模拟储藏实验材料及样品处理

取自黑龙江的粳稻样品，采用喷雾加无菌水方式，将样品水分含量调至目标水分，密封于4 ℃低温均衡水分。目标水分含量较高的样品，需多次加水，低温均衡水分时间至少30 d，直至稻谷含水量含量达到目标水分并通过水分均匀性检验。

1.2 试剂和仪器

HPS-250生化培养箱；PL3002-IC电子分析天平；SMART显微镜。

1.3 实验方法

1.3.1 模拟储藏及检测周期

将不同水分含量(13.0%、13.5%、14.0%、14.5%、15.0%、15.5%、16.0%、16.5%、17.0%、17.9% )的稻谷样品，密封并分别置于不同温度的(10、15、20、25、30、35 ℃)生化培养箱中模拟储藏180 d，每10 d取样一次，检测储粮真菌生长数量。

1.3.2 稻谷实仓情况及取样方法

选择华北地区某粮库稻谷仓为实验仓。稻谷仓基本信息：2017年1月入库，产地黑龙江，容量6 000 t，入仓水分为14.5%。取样位置的选择与粮情检温电缆表层布点位置相重合，具体分布如图1所示。取样深度为距离粮面0.4 m深度。度夏期间采用手动扦样器定期取样，每次取样200 g，置于无菌袋中保存，取回后4 ℃低温保存，以备检测。

图1 实验仓扦样点位置示意图

1.3.3 储粮真菌检测方法

参照LS/T 6132《粮食检验 储粮真菌的检测 孢子计数法》。

1.3.4 稻谷含水量测定方法

参照GB/T 5497 粮食、油料检验水分测定法 105 ℃烘干法。

1.3.5 粮温检测方法

参照粮库内粮情检测系统表层粮温数据。

1.4 数据处理方法

1.4.1 真菌生长数据预处理方法

本实验设置了10个水分梯度的稻谷样品，6个模拟储藏温度，180 d中，对每个梯度的样品每10 d取一次样，检测储粮真菌生长数量，共取19次，总计1 140组数据，每次取样做双实验，两次结果偏差超过50%时，重新取样检测，检测结果取平均值。

真菌孢子数在103～107个/g范围，且微生物生长为非线性，根据微生物生长模型处理经验[10]，对真菌孢子数进行对数变换，不仅利于线性回归，而且可以缩小数据的绝对值以方便数据处理，降低样本的异方差程度[11]。真菌检测方法的检出限为3×104个/g，对于未检出真菌生长的样品，并不代表粮食不携带真菌孢子，而是孢子浓度未达到该方法检出限，依据环境及正常粮食真菌带菌量经验数据[12]，将该方法未检出的稻谷样品带菌量补为1×103个/g，更符合稻谷带菌量的实际情况。

1.4.2 数据分析软件

文中数据结果由MATLAB2016软件处理获得。

2 结果与讨论

粮食储粮真菌的生长受多个因素的影响。多元线性回归模型，可以实现多个自变量的最优组合共同来预测或估计因变量。其主要步骤如下：第一步，确定自变量和因变量；第二步，根据研究现象，依据相应的理论和经验，设定模型并加以确定；第三步，参数估计；第四步，模型的检验和修正，常用的检验有拟合优度检验、线性回归模型F检验、参数的t检验以及残差分析。第五步，模型的运用[13]。下面重点介绍建模、模型检验及应用。

2.1 多元线性回归建模

多元线性回归是一种数理统计方法，设因变量为y，自变量为x，自变量有p个，它们的n组观测值为(x1i，x2i，xpi，yi)(i=1，2，…，n)，其多元线性回归表达式如下所示：

β是多元线性回归方程的系数。

在数据分析过程中，将所得实验数据导入MATLAB，分别绘制出取对数后的真菌孢子数与环境温度，稻谷含水量和储藏时间的散点图，见图2。

从图2中所示的散点图可看出，取对数后的真菌孢子数分别与环境温度、稻谷含水量和储藏时间大致呈线性关系。因此，可以利用MATLAB对其进行多元线性回归。

本研究对上述实验采集的1 140组实验数据，将稻谷储藏温度、含水量、储藏时间作为自变量，取对数处理的真菌孢子数作为因变量，用MATLAB软件regress语句对这些实验数据进行拟合，得到的多元线性回归模型如下：

图2 取对数后真菌孢子数与环境温度、储藏时间及稻谷含水量的散点图

lny=-20.787+0.157×x1+0.027×x2+1.683×x3

(1)

式中：y表示真菌孢子数，单位为个/g；x1表示环境温度，单位为℃；x2表示储藏时间，单位为d；x3表示稻谷含水量，以%表示。

式(1)为以lny为因变量的多元线性方程，对方程(1)进行指数变换，得到以y为因变量的指数函数方程。

y=exp(-20.787+0.157×x1+0.027×x2+1.683 ×x3)

(2)

2.2 预测模型的效果分析

根据实验数据初步建立了多元线性回归模型，还须通过模型的拟合优度、方程线性关系的显著性、系数的显著性等统计量的检验后，才可以用于解释、分析实际问题[14]。

2.2.1 拟合优度检验

拟合度是用于检验回归方程对样本观测值的拟合程度。多元线性回归的拟合程度，使用多重判定系数，其定义为：

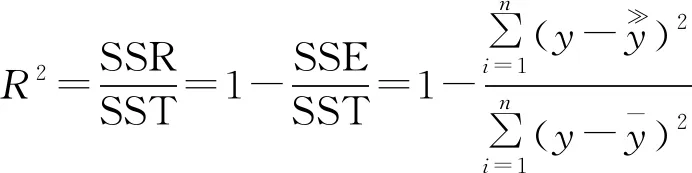
式中: SSR为回归平方和，SSE为残差平方和，SST为总离差平方和。R2表示因变量与所有自变量之间的线性相关程度，实际反映的是样本数据与预测数据间的相关程度，R2越接近于1，方程拟合优度越高[15]。R2的平方根称为复相关系数(R)，本模型的相关系数R= 0.878，判定系数R2= 0.770，这说明取对数后的储粮真菌孢子数的变化有77%可由环境温度、稻谷含水量和储藏时间这三个因素的变动来解释。

2.2.2 线性关系显著性检验(F检验)

在建立多元线性回归模型之后，还必须对因变量与多个自变量间的线性关系的假设进行显著性检验。F统计量定义为：平均的回归平方和与平均的残差平方和之比，对于多元线性回归方程：

式中: SSR为回归平方和;SSE为残差平方和;n为样本数;k为自变量个数。F统计量服从第一自由度为k、第二自由度为n-k-1的F分布，即F～F(k，n-k-1)。通过查询F分布分位数表，我们可以得出特定显著度条件下F检验的临界值。当统计量F的值大于临界值时，即可认为在总体上自变量与因变量呈显著的线性关系。F值越大，线性回归效果越显著。

在本模型的F检验中，总平方和为15 150.32，回归平方和为11 667.82，残差平方和为3 482.50。本研究显著性检验的显著性概率值为0，显然满足P<α=0.05。F统计的观测值为1 219.552，查表得F0.05(3，1 136)= 2.61，F值远大于F0.05(3，1 136)，表明因变量与自变量之间整体线性关系显著，即取对数后的真菌孢子数与环境温度，稻谷含水量和储藏时间存在显著多元线性关系。

2.2.3 回归系数显著性检验(t检验)

在多元线性回归方程中，回归方程显著性F检验和回归系数t检验是不等价的，还需进行方程回归系数的t检验，以判断各相关因子之间是否存在共线性现象。统计量t定义为：

给定一个显著性水平α，可以从t分布分位数表查得tα/2(n-k-1)。当|ti| >tα/2(n-k-1)，P<α=0.05，接受备择假设H1。本模型各项变量的t显著性概率均为0，均小于0.05，环境温度、储藏时间和稻谷含水量的t统计量分别为24.785、27.175、46.607，均大于t0.025(1 136)= 1.96。由此可见，稻谷含水量、储藏时间和环境温度对取对数后的储粮真菌孢子数均有显著影响。

2.2.4 残差分析

残差是实际观察值与回归估计值的差。从残差图可以看出数据的残差离零点的远近，当残差的置信区间均包含零点，说明回归模型能较好的符合原始数据，否则视为异常点。

对1 140组实验数据进行残差分析后的残差图如图3所示，由此可以确定残差落在其置信区间内的大致位置，也可以观察残差的分布变化的趋势，残差图越散乱代表模型的适配越好[16]。经分析，异常点主要分布在35 ℃、13%水分下储藏5个月后和35 ℃、13.5%水分下储藏4个月后的数据点，以及高温高水分储藏条件下的储藏初期数据点，共计44组数据。这些异常数据中，高温低水分区(13.0%和13.5%)真菌孢子数量基本处于检测方法的最低检出限附近，检测结果误差偏大，高温高水分区(17.9%)，储粮真菌生长速度较快，10 d的取样频率，无法检测到真菌孢子数量逐渐升高的趋势，因此初期检测数据波动较大，影响模型的准确率。经过一次残差分析，剔除异常点后，模型的拟合度R2从0.72上升到0.77。若经过多次筛选完全剔除异常点后，拟合优度能达到0.84，但此时的结果是为了达到数学上的最优化而剔除了一部分符合实际的实验数据，可能影响模型的真实性，因此选择第一次剔除异常点后的数据点进行拟合建模。

2.3 实仓检测数据验证

为了便于对真菌生长预测模型在实际应用中预测效果进行评价，根据标准“LS/T 6132 粮食检验 储粮真菌的检测 孢子计数法”[17]附录C“储粮安全评价参考表”，将危害真菌孢子检出数量分为4个级别，详见表1。在实际储藏中，储粮样品真菌孢子检出数量基本可代表粮食样品霉变程度，依据参考表中级别对储粮安全状况进行初步判定，进而指导相应处置措施。

表1 储粮安全评价参考表

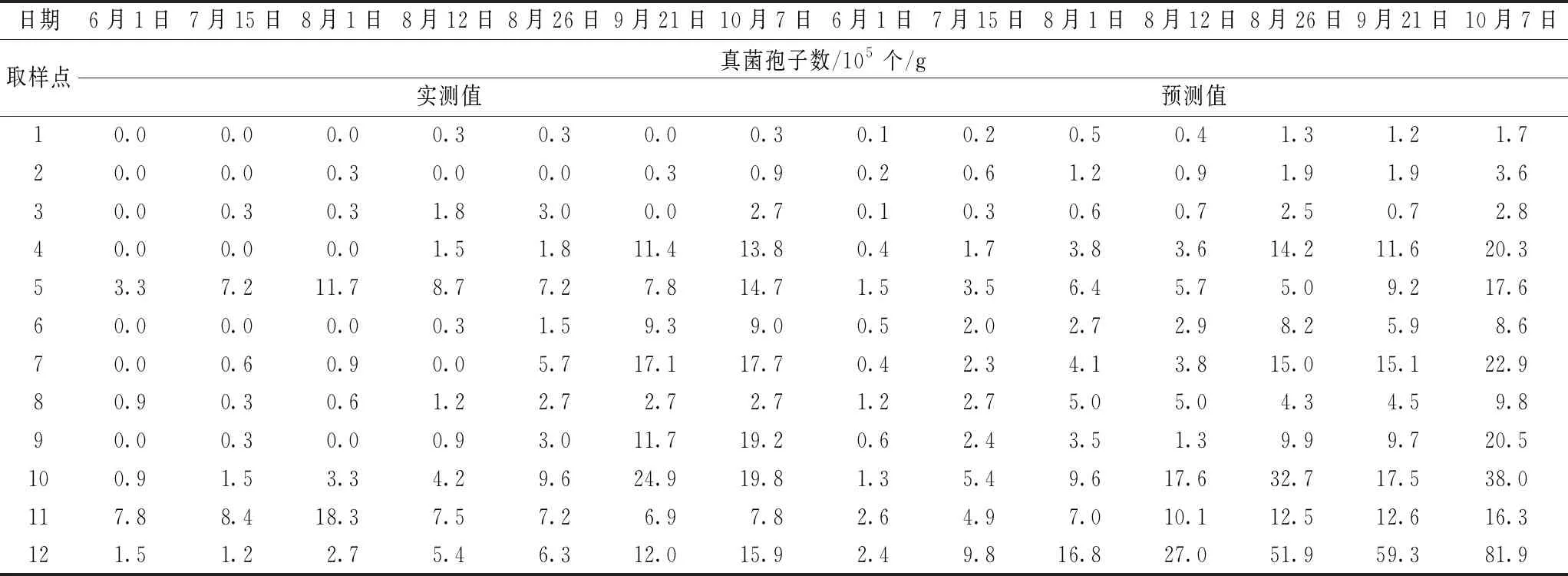
实仓检测数据来源于华北地区某粮库，实验仓详细储粮信息及采样方法见方法1.3.2。检测时间从6月到10月，对应粮食储藏时间为150 ～ 255 d，温度范围为19.0～ 27.4 ℃，水分范围为12.8% ～ 15.4%，共计84组实仓检测数据，根据实仓测得的温度、稻谷含水量和储藏时间，采用式(2)对实仓储粮真菌孢子数进行预测，实测数据与预测数据结果见表3。

由于微生物生长检测方法本身误差很大，对真菌孢子数量进行预测，预测值与实测值在同一个数量级以内，不影响储粮安全级别评价，可指导合理的应急处置措施，即认为可以接受。实测数据与预测数据结果如表2所示，84组实仓数据中，有70组数据在同一个数量级内，对储粮安全评价级别在同一级内，即对各点储粮真菌危害程度预测正确率为83.3%。由此可见，通过多元线性回归方法得到的储粮真菌生长数量预测模型为实仓储粮安全状况预测提供了一个新的方法和途径。

图3 第一次残差分析结果

表2实仓检测数据与预测数据比较

日期6月1日7月15日8月1日8月12日8月26日9月21日10月7日6月1日7月15日8月1日8月12日8月26日9月21日10月7日取样点真菌孢子数/105个/g实测值预测值10.00.00.00.30.30.00.30.10.20.50.41.31.21.720.00.00.30.00.00.30.90.20.61.20.91.91.93.630.00.30.31.83.00.02.70.10.30.60.72.50.72.840.00.00.01.51.811.413.80.41.73.83.614.211.620.353.37.211.78.77.27.814.71.53.56.45.75.09.217.660.00.00.00.31.59.39.00.52.02.72.98.25.98.670.00.60.90.05.717.117.70.42.34.13.815.015.122.980.90.30.61.22.72.72.71.22.75.05.04.34.59.890.00.30.00.93.011.719.20.62.43.51.39.99.720.5100.91.53.34.29.624.919.81.35.49.617.632.717.538.0117.88.418.37.57.26.97.82.64.97.010.112.512.616.3121.51.22.75.46.312.015.92.49.816.827.051.959.381.9

本研究通过模拟储藏条件得到的储粮真菌孢子数量静态预测模型，但在实际仓储环境中，由于粮堆体积较大，不同季节环境温湿度的变化，与实验室模拟的储藏条件存在较大差异，模型预测结果仍存在一定偏差。因此，有待于通过大量实仓检测数据反馈验证，优化模型算法形成新的动态预测模型，模型预测的准确率会进一步提高。

3 结论

以多元统计分析作为基础与前提，利用MATLAB软件对1 140组模拟储藏稻谷的温度、水分、储藏时间及取对数后的真菌孢子数进行多元线性回归分析，检验、分析多个自变量对因变量的综合线性影响的显著性，建立了多元线性回归模型应用于储粮真菌生长数量预测。

经残差分析剔除异常点后得到多元线性模型：

lny=-20.787+0.157×x1+0.027×x2+1.683×x3

多元线性拟合优度R2=0.77，F检验的统计量值为1 219.552，且显著性概率为0，结果表明回归模型总体效果显著；环境温度、储藏时间和稻谷含水量的t统计量分别为24.785、27.175、46.607，各项参数对取对数后的储粮真菌孢子数有显著影响。由多元线性回归模型的系数可知，对稻谷储粮真菌孢子数量影响最大是稻谷含水量，其次是储藏温度和储藏时间。

通过对多元线性回归方程进行指数变换，可得到储粮真菌孢子数的预测模型:

y=exp(-20.787+0.157×x1+0.027×x2+1.683 ×x3)

为了探究真菌孢子数量模型在实际应用中的预测效果，利用实仓数据对模型进行初步验证，以储粮安全等级作为评价标准，储粮真菌危害程度预测的正确率为83.3%。但仍有待于经过大量实仓检测数据验证，优化算法建立新的动态预测模型，进一步提高储粮安全状况预测的正确率。