原油闪点预测模型的研究

王焕维，俞 英，景冬莲，商 杰，黄海燕*

(1.中国石油大学（北京）理学院重质油加工国家重点实验室，北京 102249；2.广西出入境检验检疫局危险品检测技术中心，广西 南宁 536008)

闪点是衡量可燃性液体引发火灾危险的重要参数，是划分可燃液体危险级别的重要依据，对可燃液体的运输、储存安全有着指导性的作用。可燃液体的闪点通常采用开口杯法和闭口杯法来测定。然而，有机化合物以及其混合物的种类繁多，结构复杂，很难做到逐一测量。目前针对各种有机化合物以及简单的混合物体系，已经有研究人员提出较为准确的预测方法及理论模型，主要分为三类[1]：

（1）经验关联计算法。这种方法往往使用物质的沸点、密度、以及标准汽化焓等能体现化合物挥发性的性质[2]，作为输入变量来预测闪点。Bodhurtha[3]针对烃类物质提出了正常沸点与闪点的简单线性关系。Catoire和Naudet[4]以沸点、标准汽化焓以及碳原子数作自变量，通过非线性拟合预测化合物的闪点。冯李立等[5]以210种有机物的沸点为输入变量，闪点为预测目标值，建立了BP神经网络预测模型。基于沸点的非线性闪点预测模型还有Affen[6]、Butler[7]、Prugh[8]、Hshieh[9]等，但是上述几种方法均只适合用于预测特定种类的化合物。

（2）基团贡献法（GCM）。该方法以分子中各基团的种类和数目为依据，常用于预测有机化合物及简单混合体系的理化性质，Dai等[10]基于GCM提出了预测酯类闪点的多元线性回归（MLR）方法，均方误差根为5.371K。Wang等[11]提出了有机硅化合物的二阶多项式预测模型。Jia等[12]使用二阶基团贡献模型对287种有机化合物的闪点进行预测，平均绝对偏差为3.77K，平均相对偏差为1.16%。Albahri等[13,14]以分子中各基团数目为输入变量，分别以多元非线性回归模型和人工神经网络模型预测化合物闪点。同样提出非线性GCM模型的还有Serat等[15]和Pan等[16,17]。

（3）定量结构-性质关系（QSPR）技术。QSPR技术通常分为优化分子结构、计算选择描述符、建模、验证与解释根据几步，其模型构造清楚、意义明确、稳定性强有良好的普适性，近年来受到了广泛关注。潘勇等[18,19]和李冀等[20]将QSPR技术分别与神经网络、支持向量机结合搭建脂肪醇的闪点模型。Katritzky等[21]选取静电作用、氢键作用等电子描述符搭建QSPR模型，复相关系数达到0.978。

现有大量闪点预测研究都是针对有机物纯物质或者简单的混合体系展开的，对于原油这类组成复杂，差异性大，稳定性差的复杂混合体系，鲜有提出准确的闪点预测模型；近些年以神经网络为代表的数据驱动模型用于闪点预测获得较高关注，神经网络具有很强的学习、适应以及非线性函数逼近能力，能够很好的克服原油组成复杂带来的预测困难。

本文选取油品的恩式馏程温度、密度（20℃）、粘度（20℃）为输入变量，采用多元线性回归、BP人工神经网络、径向基函数（RBF）神经网络三种方法建模，预测油品的闪点，并对比三种模型的预测结果，比较各方法的优劣势。

1 数据预处理

本实验广泛选取各地区共计102种油样的恩氏馏程温度、20℃密度、20℃粘度作为输入变量X1、X2、X3、X4、X5、X6、X7、X8、X9，选取闪点实验值作为预测目标值Y，选用多元性线性回归法（MLR）、BP神经网络模型、径向基函数（RBF）神经网络模型分别进行预测。将其中55组样本数据列于表1。

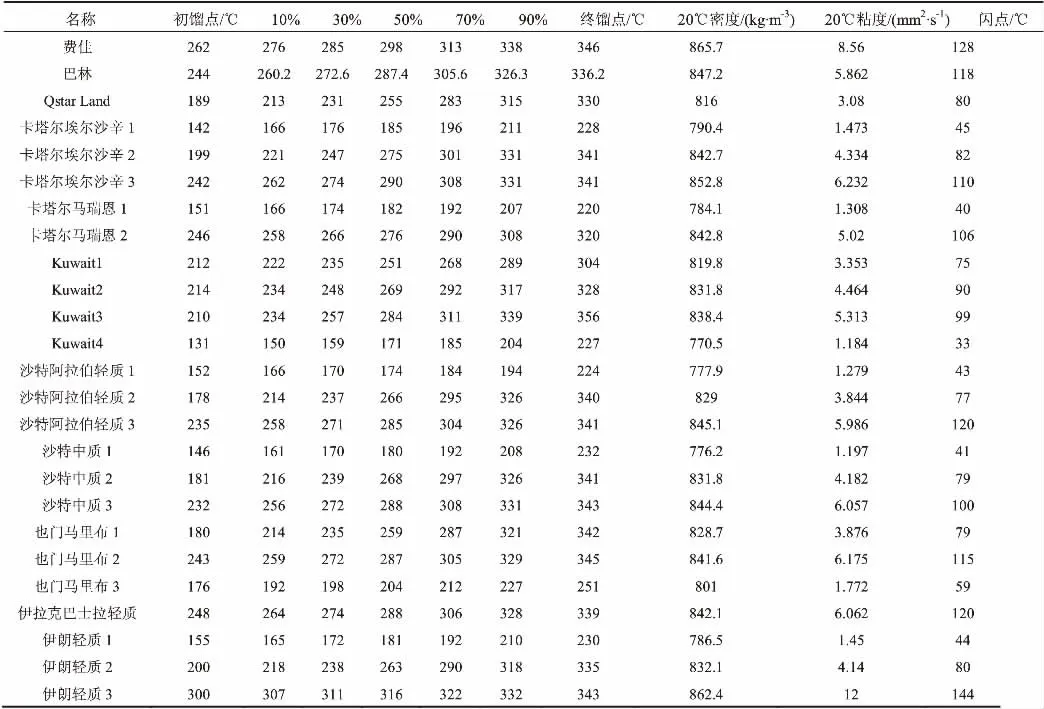
表1 各地区原油的恩氏蒸馏数据

续表1 各地区原油的恩氏蒸馏数据

利用SPSS软件检验恩氏蒸馏温度系列变量X1、X2、X3、X4、X5、X6、X7之间的相关性，得到相关系数矩阵如表2。

表2 恩氏蒸馏温度系列变量相关系数

从表2可以看到，各馏出温度之间存在很强的相关性，存在大量的信息重叠，直接用于建模，将会增加模型的计算复杂度，并且过多的自变量个数容易导致模型的过拟合现象，降低模型的泛化性能。因此有必要对变量进行简化，本论文选用主成分分析（Principal Component Analysis，PCA）对数据进行降维。

首先对变量进行标准化，构造变量矩阵令：

式中：p=1,2,…,m，这里m=7，每个样品可表示为Xi=(xi1,xi2,……,xip)T，i=1,2,…,n，这里n=102。令：

表3 主成分系数矩阵

在接下来的模型预测中，将选用主成分F1，F2以及密度（20℃）、粘度（20℃）作为新的输入变量矩阵X：

2 油品闪点的预测

2.1 多元线性回归法（MLR）建模分析

采用多元线性回归方法（MLR）建立油品恩氏馏程温度、密度（20℃）、粘度（20℃）和闪点之间的线性关系模型；以上一节数据预处理得到的主成分1、主成分2、以及密度（20℃）、粘度（20℃）作为输入变量X1，X2，X3，X4，闪点为因变量Y进行建模。将102种原油随机划分为两组，第I组92种原油用作训练集，第II组10种原油为外部测试集，以外部测试集运行结果检验模型预测能力。

首先用第I组的92种原油作为训练集，原油闪点的多元线性回归运行结果见表4。用所建立模型预测第II组10个油品的闪点，结果见表5。以实验值为横坐标，MLR预测值为纵坐标作图1。平均相对误差ARE=5.26%，平均绝对误差AAE=4.19℃，均方误差MSE=22.45。

表4 原油闪点的多元线性回归运行结果

表5 MLR闪点模型测试集验证结果

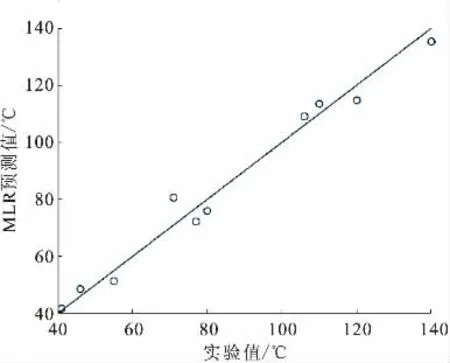
图1 MLR闪点模型外部测试集验证结果

2.2 BP神经网络法建模分析

BP-ANN网络模型由输入层、隐藏层、输出层构成，隐藏层可以根据需要定为单层或者多层，本次模拟为单层隐藏层；输入层包含4个神经元即4个输入变量，隐含层包含11个神经元，输出层包含1个神经元即闪点预测值，如图2。

图2 BP-ANN模型框架图

以Z1J为输入值通过激活函数得到隐含层的输出值A2j：

以Z2J为输入值通过激活函数的到输出层的输出值即闪点的预测值Y^。

取代价函数为J(W),W=（w1,w2,…wn）为各层输入值的权值向量：

通过迭代不断更新权值W，

称为权值更新的步长，在本实验中取α=0.001，通过梯度下降法，在代价函数J(W)取得最小值处确定预测模型。

表6 BP-ANN闪点模型外部测试集验证结果

同样将102种原油随机划分为两组，第I组92种原油用作训练集，第II组10种原油为外部测试集，为比较各模型优劣，BP-ANN、RBF-ANN均沿用多元线性回归（MLR）的随机分组结果，以测试集运行结果检验模型预测能力。原油闪点预测运行结果见表6，以实验值为横坐标，BP-ANN预测值为纵坐标作图，结果如图3所示。预测结果显示平均绝对误差为3.44℃，平均相对误差为4.27%，均方误差MSE=13.37。

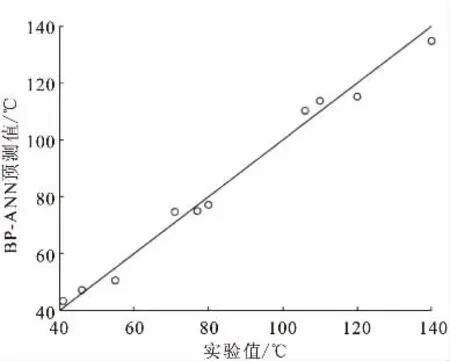
图3 BP-ANN闪点模型外部测试集验证结果

图4 均方误差曲线

由图4可以看到，本次逼近共进行11次迭代，过程中训练集均方误差单调递减，验证集均方误差（MSE）在第5次迭代取得极小值。

图5 整体拟合曲线

从图5可以看出训练集、验证集、测试集、总体的拟合都较好，不存在过拟合现象。

2.3 RBF神经网络法建模分析

RBF-ANN是一种三层静态前向网络，由输入层、隐藏层、输出层构成，如图6所示，用径向基函数（RBF）作为隐藏层神经元的“基”构成隐藏层空间，从输入层到隐藏层，可以将输入矢量直接映射到隐藏空间，而不需要分配权值来连接，一旦RBF的中心确定，输入层到隐藏层的映射关系也就确定了；隐含层空间到输出层空间的映射是线性的，其权值可以通过递推最小二乘法由方程组的形式求出。

图6 RBF-ANN模型框架图

与BP神经网络不同的是，RBF-ANN输入层到隐藏层的映射不需要计算机初始化来分配权值，而是通过计算各样本点到各中心的距离得到输入的“权值”，这里的距离常常采用欧式距离||x-cn||，在各中心通过径向基函数，这里选用高斯函数，即：

这里x为m维输入向量，cn是该网络的第n个中心，是与x具有相同维数的向量。

φn（x）作为隐隐藏层的输出，通过线性加和得到预测值μ（x）：

可以看出RBF网络的优劣依赖于RBF中心的选取，包括中心数目、位置、以及作用宽度。选取RBF中心的方法有多种，这里选择有监督学习的方式选取RBF中心，RBF中心以及网络的其他可变参数均通过有监督学习实现，其中监督学习将采用梯度下降法来迭代实现。其目标函数为：

其中m为样本数，n为RBF中心数。通过梯度下降，对可变参数wi，ci进行迭代，使目标函数τ达到极小值从而得到最优模型。

同样将102种原油随机划分为两组，第I组92种原油用作训练集，第II组10种原油为测试集，以测试集运行结果检验模型预测能力。原油闪点预测运行结果如表7，以实验值为横坐标，MLR预测值为纵坐标作图，结果见图7。

表7 RBF-ANN闪点模型外部测试集验证结果

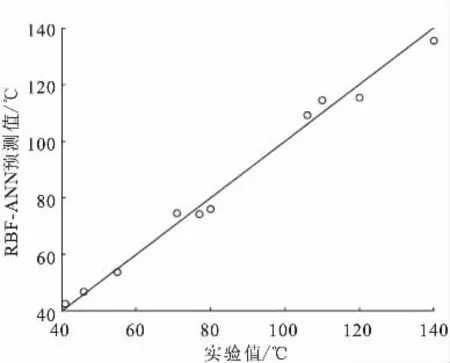
图7 RBF-ANN闪点模型外部测试集验证结果

预测结果显示平均绝对误差为3.08℃，平均相对误差为3.58%，均方误差MSE=11.30。

2.4 不同预测模型方法的对比

将102种原油随机划分为两组，第I组92种原油用作训练集，第II组10种原油为外部测试集，分别用多元线性回归（MLR）、BP神经网络、RBF神经网络进行建模，并用第二组外部测试集验证运行结果。

为更好的比较模型的准确性与稳定性，将上述步骤重复10次，得到10组运行结果如表8所示。

表8 10组重复试验运行数据

重复试验结果显示，多元线性回归（MLR）模型的相对误差的期望为4.82%，绝对误差的期望为3.79℃。BP神经网络模型的相对误差的期望为4.05%，绝对误差的期望为3.33℃。RBF神经网络模型的相对误差的期望为3.49%绝对误差的期望为2.94℃。可以看出RBF-ANN模型预测结果的相对误差期望最低，准确性最优，BP-ANN准确性比RBFANN稍差，优于MLR。

多元线性回归（MLR）模型预测结果的均方误差（MSE）的方差为37.22，BP神经网络模型预测结果MSE的方差为51.26，RBF神经网络模型预测结果MSE的方差为10.76。将各组均方误差绘于图8，可见RBF-ANN预测模型的稳定性最好，BP-ANN预测模型的稳定性最差，这与BP神经网络的目标函数易于陷入局部极小值有关。

图8 各组外部测试集均方误差MSE

3 结论

针对原油复杂混合体系，以原油恩氏蒸馏温度、20℃密度、20℃粘度作为输入变量，通过主成分分析法对输入变量进行降维，采用多元线性回归（MLR）、BP神经网络、RBF神经网络三种方法建模，预测结果表明：多元线性回归（MLR）模型的相对误差的期望为4.82%，绝对误差的期望为3.79℃，可以看出恩氏蒸馏数据、密度、粘度与闪点有着较好的线性相关性，但是预测准确度不够。采用BP神经网络建模，预测结果的相对误差期望为4.05%，绝对误差的期望为3.33℃，准确度较多元线性回归模型有较大提升，但是其均方误差MSE起伏较大，模型的稳定性不够好，这是因为BP神经网络在进行梯度下降时，目标函数容易陷入局部极小值。采用RBF神经网络建模，其相对误差的期望为3.49%绝对误差的期望为2.94℃，可以看出RBF-ANN模型的误差最低，准确度最优。并且均方误差MSE的期望与方差均为最低，稳定性也优于MLR与BP-ANN模型。RBF神经网络模型属于局部逼近，并且输入层到隐含层的输入由样本到RBF中心的距离计算得到，不需要迭代不会陷入局部极小，计算效率高。改良输入变量的选取或者RBF中心的选取方法，将进一步提高预测的精度。