基于利维飞行和变异算子的萤火虫算法
何 栎,姚青山,李 鹏,姜天琳
(1. 河南工程学院 计算机学院,河南 郑州 451191;2. 河南省智慧建筑物联网工程研究中心,河南 郑州 451191)
0 引 言
受萤火虫社会行为的启发,标准萤火虫算法(stan-dard firefly algorithm,SFA)由Xin-She Yang[1]提出。SFA是一种基于萤火虫闪光特性行为的群体技术。由于萤火虫算法(firefly algorithm,FA)操作简单,参数设置较少,在优化工程实践中得到了广泛的应用。为提升萤火虫算法性能,多种策略被用于调节算法的控制参数,多种优化方法与SFA结合[2]。光强差用于自适应调节FA参数[3];邻域吸引力用来防止搜索过程中的振荡和较高的计算时间复杂度[4];潮汐力公式已被用于修改FA,并在功能适应性的探索与开发之间保持平衡[5]。FA的理论分析已经开展[6]。
为了进一步加强FA算法的全局搜索能力和避免陷入局部最优,提出了一种基于利维飞行和变异算子的萤火虫算法(levy flight and mutation operator based firefly algorithm,LMFA)。当萤火虫不能提高自身解的质量超过一定的次数后,萤火虫的位置将借助利维飞行进行重分布,若结果依然没有改善,变异算子将用于扩大萤火虫的多样性并改进解的质量。LMFA在广泛采用的基准函数上的测试结果在多数情况下优于其它5种代表性的FA算法。
1 FA,利维飞行和变异算子
1.1 FA
萤火虫通过有效化学反应发光。光线被用来吸引猎物和异性成员,并警告食肉动物。雄性萤火虫在寻找配偶时,会以一定的模式进行闪光,吸引周围雌性萤火虫。感兴趣的雌性萤火虫会回答,帮助雄性萤火虫找到其休息的地方。萤火虫的闪光是一个信号系统,可以与待优化的目标函数相关联[1]。
我们首先描述标准萤火虫算法SFA,然后介绍其改进算法。
在SFA[1]中,每个萤火虫都向更亮的萤火虫学习以更新自己的位置。令Xi=[xi,1,xi,2,…,xi,D] 表示第i个萤火虫的位置,其中i=1,2,…,N。 令G=[g1,g2,…,gD] 表示种群中最优的萤火虫位置。萤火虫的亮度由目标函数决定。萤火虫的吸引力与相邻萤火虫的光强度成正比。吸引力β定义为
(1)
其中,β0,γ,rij分别是预定义的吸引力,光吸收系数,萤火虫i和j之间的距离[1]。第i个萤火虫被另一只更亮的第j个萤火虫所吸引。第i个萤火虫的位置更新如式所示
xi,d=xi,d+β·(xj,d-xi,d)+α·sd·εi,d
(2)
其中,α表示一个随机参数,sd表示一个参数,εi,d服从某种随机分布,缺省情况下服从均匀分布。
SFA的流程如算法1所示,其中f(X)是目标函数,N是种群大小,FEs是适应度评估次数,MAX_FEs是适应度最大评估次数。
算法1:标准萤火虫算法FA
(1) 目标函数f(X),X=[x1,x2,…,xD];
(2) 萤火虫种群初始化Xi(i=1,2,…,N);
(3) 计算每个萤火虫的适应度值f(Xi);
(4)FEs=N;
(5)whileFEs≤MAX_FEsdo
(6)fori=1 toNdo
(7)forj=1 toNdo
(8)iff(Xi)>f(Xj)then
(9) 根据式(2)将Xi移向Xj;
(10) 计算更新后Xi对应的适应度值;
(11)FEs++;
(12)end
(13)end
(14)end
(15) 对萤火虫进行排序并且找出种群中最佳萤火虫;
(16)end
(17) 对萤火虫进行后处理和可视化.
1.2 利维飞行
动物和昆虫的飞行行为已经在许多研究中得到了分析。这种飞行行为已经应用于优化和搜索算法中,研究结果表明其在搜索算法领域的重要性[7-9]。
利用利维飞行策略改进了许多算法的搜索过程。将式中εi,d设置为服从利维分布,结果表明,基于利维飞行的FA以更高概率更有效地找到全局最优[10]。利维飞行搜索策略和反向学习(opposition based learning)应用于差分进化算法,在大多数情况下新算法在可信度、有效性、准确性优于基本DE[8]。当粒子在有限时间内不能改进自身解时,粒子在搜索空间中采用利维飞行方法进行重新分配[7]。
利维飞行是从利维稳定分布中抽取的一类随机漫步方法。利维飞行Levy(λ)可以如式进行计算[11]
(3)
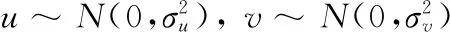
(4)
其中,Г服从标准Gamma分布。
1.3 变异算子
遗传算法是一种基于自然选择的求解有约束和无约束优化问题的方法。在从当前种群创建新种群的每个步骤中,有3种基本算子:选择算子选择对下一代群体有贡献的个体;交叉算子将两个父代结合起来,形成下一代个体;变异算子对父代个体应用随机变化来形成子代。生物实验结果表明,生物的行为和遗传信息是相互影响的。变异算子引入随机修改,其目的是保持种群的多样性和抑制过早收敛[12,13]。变异算子在搜索空间中引入了随机漫游。变异算子在遗传算法、遗传设计算法和混合遗传算法等群体智能算法中都有应用[12,14]。
2 基于利维飞行和变异算子的萤火虫算法(LMFA)
2.1 利维飞行和变异算子方法
我们提出一种算法,即基于利维飞行和变异算子的萤火虫算法(Levy flight and mutation operator based firefly algorithm,LMFA)。一般情况下,萤火虫位置用式进行更新。如果萤火虫的适应度在一定次数(用sg表示)迭代后没有改善,可以认为萤火虫深深陷入了局部最优状态。此时,萤火虫的新状态可以这样计算
Oi=xi+Levy(λ)·randn(0,1)
(5)
其中,Levy(λ)用式(3)表示,randn是标准正态分布函数。
算法2:基于利维飞行和变异算子的萤火虫算法LMFA
(1)/*初始化 */
(2)fori=1toNdo
(3) 随机初始化Xi,Oi;ci=0; 评估f(Xi);
(4)endfor
(5)
(6)/*主循环*/
(7)Repeat
(8)fori=1toNdo
(9)f(Oi)=inf;
(10)forj=1toNdo
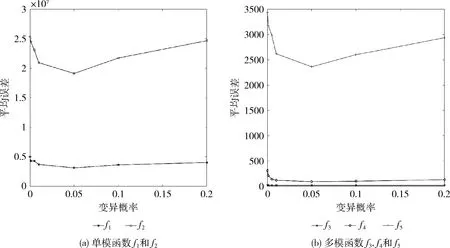
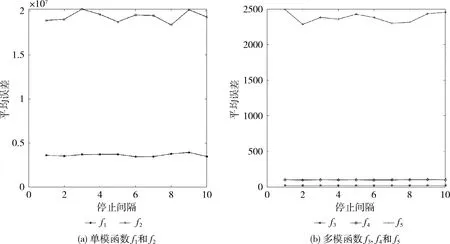
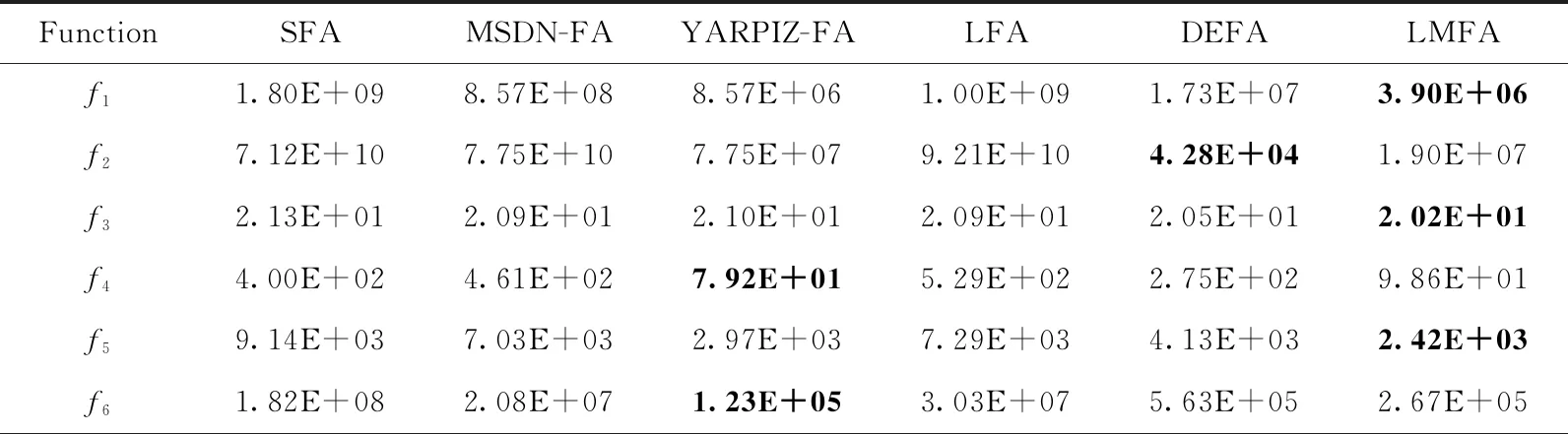
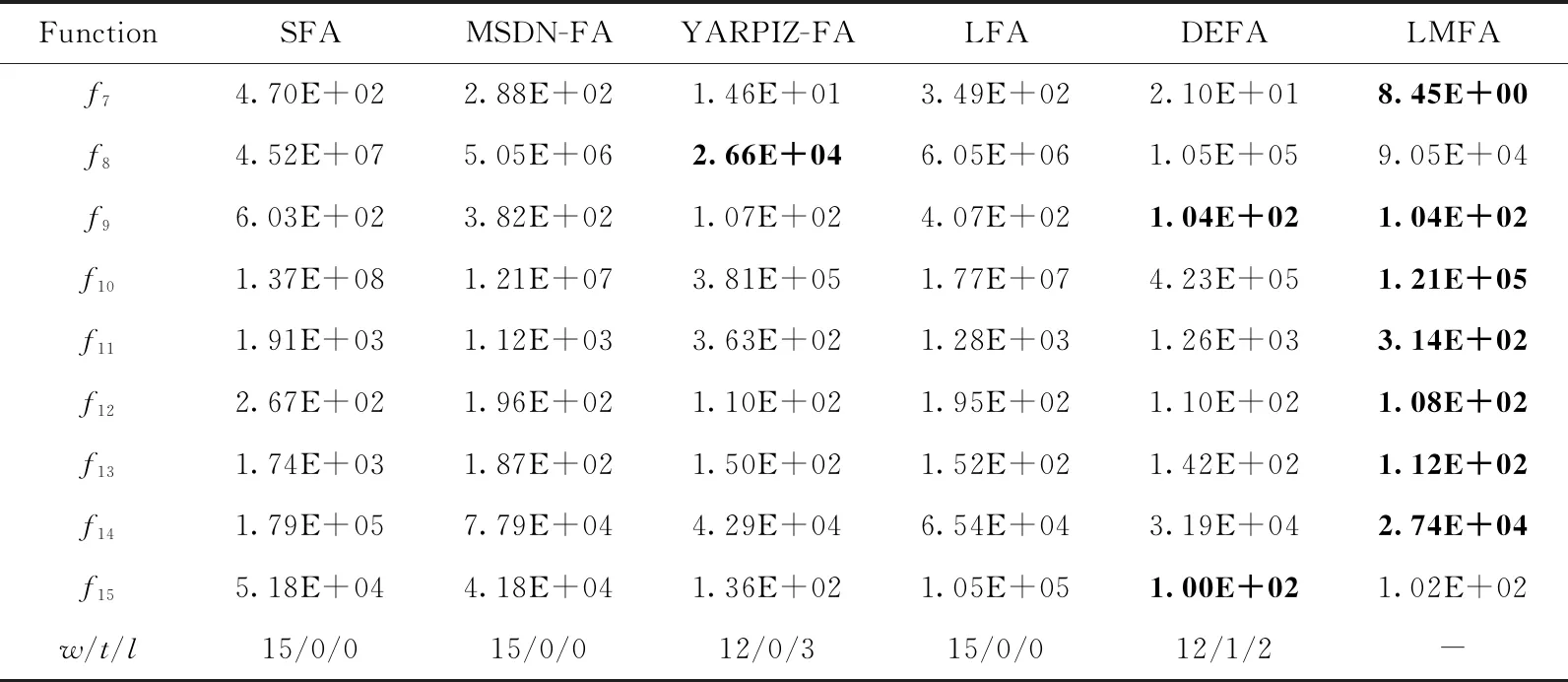
(11)iff(xj) (13)fork=1toDdo (14)tempd=xi,d+β·(xj,d-xi,d)+α·sd·εi,d; (15)endfor (16) 评估f(temp); (17)iff(temp) (18)Oi=temp;f(Oi)=f(temp); (19)endif (20)endif (21)endfor (22)endfor (23)fori=1toNdo (24)iff(Oi) (25)ci=0;xi=Oi;f(xi)=f(Oi); (26)else (27)ci=ci+1; (28)endif (29) /*经过sg次,f(xi) 停止改进*/ (30) 根据过程1进行计算 (31)endfor (32)until终止条件 过程1:利维飞行和变异策略 (1)/*经过sg次,f(xi) 停止改进*/ (2)ifci>sgthen (3) /*利维飞行*/ (4)Oi=xi+levy(λ)·randn(0,1); 评估f(Oi); (5)iff(Oi) (6)xi=Oi;f(xi)=f(Oi);ci=0; (7)else (8) /*变异*/ (9)Oi=xi; (10)forj=1toDdo (11)ifrand(0, 1) (12)oi,d=rand(lbd,ubd) (13)endif (14)endfor (15) 评估f(Oi); (16)iff(Oi) (17)ci=0;xi=Oi;f(xi)=f(Oi); (18)else (19)ci=ci+1; (20)endif (21)endif (22)endif 接着更新萤火虫的位置 (6) 如果利维飞行不能帮助萤火虫逃离局部最优状态,变异算子将被用于更新萤火虫的状态信息 (7) 其中,lbd和ubd分别是萤火虫第d维的下限和上限,pm是变异的概率。这种变异使萤火虫探索的范围更广。式(6)决定萤火虫位置是否更新。 通过利维飞行和变异算子,萤火虫能够迅速改变搜索方向,以便跳出局部最优解。 简言之,对于每个萤火虫,它像SFA一样在搜索空间中更新位置,当它遇到早熟时,采用利维飞行和变异算子寻找更优解。LMFA的伪代码如算法2所示,利维飞行和变异策略如过程1所示。可以看出,LMFA容易执行。 LMFA保留了FA的基本框架,萤火虫通过向周围更加明亮的萤火虫学习来更新自己的位置。LMFA的新颖之处在于,利用利维飞行和变异算子使萤火虫保持种群多样性,潜在地提高了萤火虫的勘探和开发能力。 LMFA的计算开销取决于萤火虫初始化Tinit、函数评估Teval、SFA的位置更新Tupda、利维飞行算子T利维、变异算子Tmuta。假设D是搜索空间的维度,MaxFEs是算法允许的最大评估次数。在最坏的情况下,我们有Tupda=D,T利维=D,Tmuta=D。 此外,SFA的位置更新、利维飞行、变异算子都会消耗评估次数,这三者的最大迭代次数是MaxFEs/3。 因此,LMFA在最坏情况下时间复杂度为T(D)=Tinit+[(Teval+Tupda)+(Teval+T利维)+(Teval+Tmuta)]·(MaxFEs/3)=D+[(D+D)+(D+D)+(D+D)]·(MaxFEs/3)=D·(1+2·MaxFEs)。 因此,LMFA的时间复杂度为O(D*MaxFEs),近似于MaxFEs。 由于参数MaxFEs通常设置为10000·D,所以LMFA的时间复杂度与空间维度D的二次方成正比。 被广泛采用的CEC2015评测函数[15]被用于测试所提出算法的性能。评测集包含15个函数,其中10个在表1中列出。所有函数都被表达为最小优化问题。评测集包含4类函数,其中f1和f2是单模函数,f3-f5是简单多模函数,f6-f8是混合函数,f9-f15是复合函数。函数f1到f15是由表2中列出的14个基本函数构成的。 表1 来自CEC的评测函数 f(x)=g1(M1z1)+g2(M2z2)+…+ (8) 复合函数的形式如式所示[15] (9) 其中,gi(x)是用于构造复合函数f(x)的第i个基本函数,N是基本函数的数量,biasi定义哪个是全局最优,λi用于控制每个gi(x)的高度,ωi是每个gi(x)的权重。 为了验证新算法的性能,LMFA与5种代表性的FA算法进行比较。这些算法的参数遵循相应文献的设置,如表3所示,其中ubd和lbd表示萤火虫在第d维移动的上限和下限。这些算法都在30维函数上进行测试,最大评估次数都设置为MaxFEs=10000D。 所有实验都是在拥有AMD Core FMTM8350 CPU 4 GHz、8G内存和安装Windows 7操作系统的计算机运行。 变异概率pm和停止间隔sg可能是影响LMFA的重要因素。pm分别取值0,0.001,0.005,0.01,0.05,0.1,和0.2,此时其它参数的值与表3保持一致。单模函数f1和f2、简单多模函数f3、f4、f5用来进行参数选取实验。不同pm设置对于LMFA的影响如图1所示,其中横轴表示pm值,纵轴表示每个函数的平均误差。可以看出,pm可以设置为0.05左右,此时LMFA在单模函数和简单多模函数上都表现比较好。 进一步进行sg对LMFA影响的实验。sg分别设置为1,2,…, 10,此时其它参数保持不变。从图2可以看出,解的准确率对停止间隔sg不是很敏感,sg取不同值,算法都表现比较好的性能。这个参数决定萤火虫的跳跃行为。一个小的sg将使得萤火虫频繁改变正常的搜索过程并导致种群震荡,而一个大的sg会使萤火虫长时间陷入局部最小值。综合考虑,pm=0.05和sg=7适合于LMFA。 表2 来自CEC的基本函数[15] 表3 参数设置 图1 变异概率pm对LMFA性能的影响 图2 停止间隔sg对LFMA性能的影响 在本节,我们将比较LMFA和其它FA算法,包括SFA[16], MSDN-FA[17], YARPIZ-FA[18], LFA[10], DEFA[19]。所有算法中一个种群由50个萤火虫构成。每个算法对每个函数测试30次,然后记录平均最好适应度。 表4汇总了这6种算法的计算结果,6个算法中最好结果用粗体表示。LMFA与其它5种FA算法的比较结果用w/t/l表示,这意味着与竞争者相比较,LMFA在w个函数上胜出,在t个函数上没有明显优势,在l个函数上落后。结果表明,SFA、MSDN-FA和LFA几乎没有为所有问题找到较好的解,并且在所有函数上都陷入局部最小值。与SFA、MSDN-FA和LFA相比,LMFA取得了更好的结果。LMFA在12个评测函数上结果优于YARPIZ-FA和DEFA,而YARPIZ-FA和DEFA分别在3个和2个评测函数上优于LMFA。 表4 SFA, MSDN-FA, YARPIZ-FA, LFA, DEFA, and LMFA的平均误差 表4(续) Friedman是非参数统计测试,用于单向重复测量的方差分析。Friedman测试用于比较所有6种FA算法在测试集上的性能。表5列出了Friedman测试中LMFA和其它5种FA算法的平均秩。最佳秩(具有最小秩)用粗体表示。可以看出,LMFA的秩最小,表明总体性能优于其它5种FA算法。 表5 6个FA算法进行Friedman 测试的平均秩 如图3所示LMFA和其它5种FA算法在多个函数上的收敛曲线。可以看出,在大多数函数上,LMFA收敛速度快于其它算法。 图3 SFA, MSDN-FA, YARPIZ-FA, LFA, DEFA, LMFA对于多个函数的收敛曲线 提出了一种FA算法,该算法采用利维飞行和变异算子来防止萤火虫陷入局部极小值。利维飞行带来了随机漫步,而变异算子则为萤火虫注入了多样化的信息,从而加强全局探索。如果萤火虫不能改善自身解,则利用利维飞行和变异算子将萤火虫重新分布到搜索空间。为了验证LMFA的性能,使用了一组具备不同特征的数值基准评测函数,并将提出的算法与几种具有代表性的FA算法进行了比较。实验结果表明,该算法在全局搜索能力、求解精度和搜索速度等方面具有优势。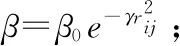

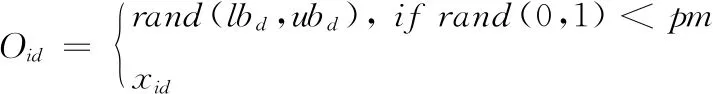
2.2 LMFA的复杂度分析
3 实 验
3.1 实验设置

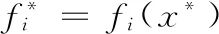
gN(MNzN)+f*(x)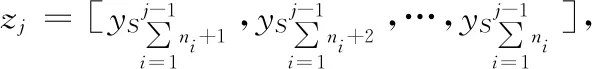
3.2 参数选取


3.3 实验结果和讨论


4 结束语

