自适应爆炸半径的改进烟花算法

赵志刚，李智梅，莫海淼，曾 敏，温 泰

(广西大学 计算机与电子信息学院，广西 南宁 530004)

0 引 言

Tan等[1]提出了烟花算法(fireworks algorithm，FWA)，该算法收敛速度快，易于实现，且具有爆发性、多样性和随机性等特点，目前被广泛应用于网络定位[2]、JSP问题求解[3]、投资组合优化问题[4]、聚类[5]等多个领域。烟花算法在应用到某些实际的过程中表现力不从心，因此众多学者对烟花算法进行改进，主要是对FWA算法的算子分析及改进以及与其它启发式算法结合成混合算法[6]。Barraza等[7]基于模糊逻辑，对爆炸火花数目以及爆炸振幅进行调整，提高了烟花算法的性能。Zhang等[8]提出了BBO-FWA算法，将生物地理学优化算法的迁移算子引入烟花算法，表现出了较强勘探能力。Babu等[9]基于粒子群算法和遗传算法的改进烟花算法来精确识别光伏(PV)模块的双二极管模型未知参数，有效地解决了这一建模问题。Bao等[10]提出了一种改进的混沌烟花算法，在求解多目标JSP问题上具有较高的准确性和鲁棒性。Xue等[11]提出了一种自适应烟花算法(SaFWA)来优化分类模型，利用4种候选解生成策略(CSGSS)来提高解的多样性。Yan等[12]提出了具有线性降维策略的动态搜索烟花算法(ld-dynFWA)，提高了算法的效平衡率和稳定性，并将其应用于求解条件非线性最优摄动CNOP问题。

以上方法没有考虑到被丢弃的爆炸火花信息利用的问题。为了更好地提高烟花算法的性能，利用被丢弃的爆炸火花的信息，改进爆炸机制，提出了一种具有自适应学习改进烟花算法。该算法从信息利用、自适应步长及种群多样性的增加3个角度对FWA算法进行改进，以爆炸火花的数目为分种群依据，利用爆炸火花的位置信息来构建爆炸半径，并对全局最优进行高斯变异。为了对改进烟花算法进行性能测试实验，选择10个比较常见的基准测试函数以及几种经典的群智能优化算法(如标准粒子群算法PSO、带高斯扰动的粒子群算法GPSO、蝙蝠算法BA、烟花算法FWA、自适应烟花算法AFWA、增强烟花算法EFWA)进行对照并分析。

1 烟花算法

烟花算法是根据烟花在夜空中爆炸的现象而提出的一种新型群智能优化算法，该算法主要包括四大部分：爆炸算子(爆炸强度、爆炸幅度和位移操作)、变异算子、映射规则和选择策略。

1.1 爆炸强度

烟花爆炸时，烟花种群的每个烟花都会生成相应的爆炸火花子种群。适应度值越好的烟花爆炸强度越大，爆炸火花的数量就越多；相反，爆炸强度越小，爆炸火花的数量就越少[13]。爆炸强度的计算如式(1)所示

(1)

式中：Si表示第i个烟花产生爆炸火花的数量；m是限制爆炸火花数量的常量；Ymax是烟花中最差适应度值的个体；f(xi)是第i个烟花的目标函数的适应度值；θ是极小的机器数；pop是指烟花种群数目。

使用式(2)来控制爆炸火花数量的大小

(2)

其中，round()为四舍五入的取整函数；α和β均为常数变量。

1.2 映射规则

在寻优的过程中，需对越界的烟花个体进行如下越界处理

(3)

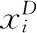
1.3 选择策略

FWA算法是基于欧氏距离来计算任意两个烟花个体间的距离，计算公式如下

(4)

其中，d(xi,xj) 是任意两个烟花xi与xj间的欧式距离；R(xi) 是烟花个体xi到其它个体的距离的总和；l∈K是第l个位置属于集合K；K表示烟花、爆炸算子和变异算子产生火花的烟花种群位置集合。

在进行下一代烟花种群选择时，其策略是采用轮盘赌的方式，与其它个体具有更远距离的烟花个体具有更大的可能性被选择，每个个体被选中的概率用p(xi)表示，即

(5)

1.4 变异算子

高斯变异是对烟花随机选择若干个维度进行操作，该操作具体为

(6)

2 改进的烟花算法

在FWA算法中，由1.3小节选择策略可知，没有被选中为下一代烟花的爆炸火花则完全被丢弃，这浪费了被丢弃的爆炸火花的信息。针对这一点，引入sparkpBest来表示在寻优过程中每个烟花所产生的最优爆炸火花个体的集合，并将其和最优烟花个体gBest来构造新的爆炸半径，同时对gBest进行变异算子操作进一步增加种群的多样性，避免烟花算法有“早熟”的情况。

2.1 新的位移操作和爆炸半径

位移操作是对烟花的每一维度进行操作，在FWA算法中，由于一个烟花爆炸时在每个维度上产生了相同位移偏移的爆炸火花，烟花算法的多样性有所降低。改进的烟花算法在烟花个体产生爆炸火花的过程中，因为使用了烟花的位置信息来构造新的爆炸半径，能够自适应地调整步长，这就使得在各个维度上可以采取不同的位移偏移来进行位移操作，其更新公式如下

xlast(l)=x(i)+r*EA(i)

(7)

其中，l=1,2,…,Si；x(i) 是第i个烟花未爆炸前的位置，xlast(l)是第i个烟花爆炸后对应子种群的第l个爆炸火花的位置；r是在[0,1]内的随机数，服从均匀分布；EA(i) 是第i个烟花爆炸产生的火花相对原始烟花的范围(烟花的爆炸半径)。

爆炸半径是指烟花个体发生爆炸之后所发生的位移，通过FWA算法中爆炸半径的计算公式可得，烟花的爆炸半径是利用烟花的适应度值来获取，这是不科学的，这是因为对于多维空间问题而言，可能会存在多个烟花的适应度值相等而位置不一样的情况，即无法判断实际的位置，因此改用位置信息。另外，根据式(4)，没有被选中为下一代烟花的爆炸火花则完全被丢弃，这浪费了被丢弃的爆炸火花的信息。针对这一点，引入sparkpBest来表示在寻优过程中每个烟花所产生的最优爆炸火花个体的集合，并将其和最优烟花个体gBest来构造新的爆炸半径，以爆炸火花数目作为分种群的依据，将烟花种群分为两类，爆炸强度小于平均爆炸强度的烟花为次好烟花，次好烟花向sparkpBest靠拢，即扩大搜索范围进行全局搜索；爆炸强度大于或者等于平均爆炸强度的烟花为优质烟花，优质烟花向此时最优烟花位置靠拢，即向当前种群最优gBest学习，在gBest附近进行详细的局部搜索提高收敛速度。

新的爆炸半径计算公式具如下所示

(8)

其中，sparkpBest(i)是第i个烟花产生的爆炸火花子种群中的个体最优；AvgS是此时所有爆炸火花的均值，即

(9)

2.2 全局最优个体的高斯变异

式(6)是随机选择几个维度来进行高斯变异，在此基础上，再对全局最优个体gBest进行高斯变异，即对该最优个体的所有维度进行变异算子操作，以便能够增加烟花算法中种群的多样性，使得改进烟花算法的全局搜索能力得到增强，提高其运算结果，具体操作如下

gBest=gBest*(N(0,1)+1)

(10)

其中，N(0,1) 是服从均值为0，方差为1的高斯分布函数。

2.3 ARFWA算法

综上所述，提出了一种改进的烟花算法，即自适应爆炸半径的改进烟花算法(improved fireworks algorithm with adaptive explosion radius，ARFWA)。ARFWA算法的伪代码如下：

步骤1 初始化烟花种群x，全局最优gBest，每个烟花所产生的最优爆炸火花个体的集合sparkpBest；

步骤2 获取每一个烟花的适应度值；

步骤3 将gBest状态更新；

步骤4 通过式(10)和式(3)对gBest前后进行高斯变异和越界处理操作；

步骤5 通过式(1)来计算烟花的爆炸强度；

步骤6 通过式(8)和式(9)来计算每一个烟花的爆炸半径；

步骤7 通过式(7)来进行位移操作，并更新sparkpBest；

步骤8 使用式(6)产生高斯火花；

步骤9 根据1.3小节的选择策略来选择下一代烟花；

步骤10 不断执行步骤2～步骤9，符合终止条件时就停止操作。

3 仿真实验

3.1 实验测试函数

为了评估改进的烟花算法在函数优化的有效性，实验选取了10个基准测试函数进行算法对比，如表1所示，包含其域，最优值以及维度信息。

表1 基准测试函数

3.2 参数设置

ARFWA算法和FWA算法的参数设置均参见文献[1]，SPSO算法参见文献[14]，GPSO算法参见文献[15]，BA算法参见文献[16]，自适应烟花算法参见文献[17]，增强烟花算法参见文献[18]。为了客观对比，7种算法的种群大小均为10，寻优精度设置为10-5。本次实验运行次数设置为100次，最大迭代次数设置为1000次。实验平台是Matlab 2016Ra，Inter(R) Xeon(R) CPU E5-1620 v3 @3.5 GHz,window10操作系统。

3.3 收敛性能分析

对表1的函数进行仿真实验，得到各个函数的求解质量，如表2所示(worst是最差值、best是最佳值、avg是平均值、std是方差值)，avg的平均排名结果见表3，寻优成功率用SR表示，见表4，各算法的寻优进化曲线图展示如图1至图10所示。为了方便对比分析，f7的适应度值是负数没有取对数，保持原始值不变，剩余函数的曲线图中纵坐标log10(Fitness)代表其适应度值均取对数log10。各函数(除了f1、f3、f4和f9外)的演化曲线出现部分重叠的情况。

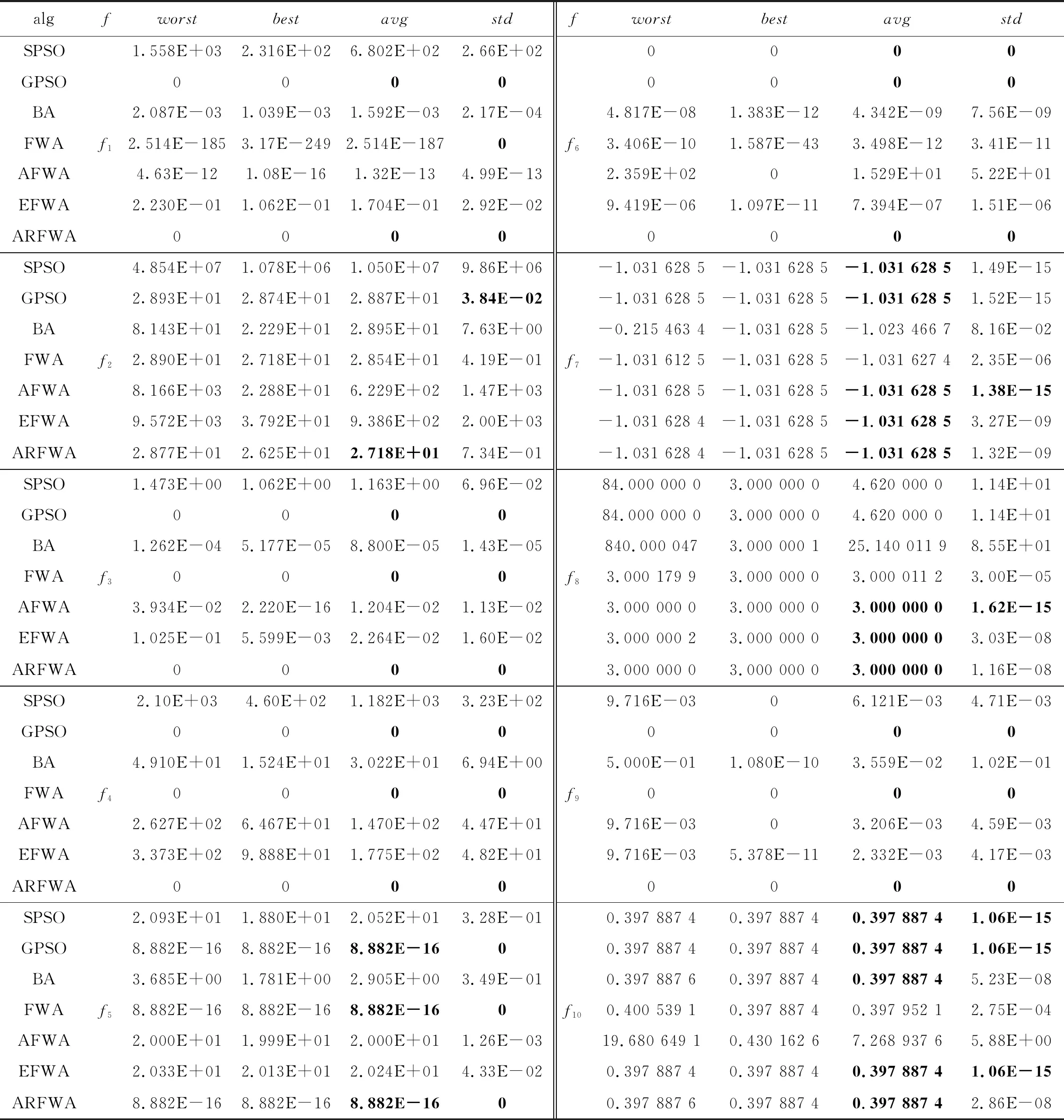
表2 各个函数求解质量

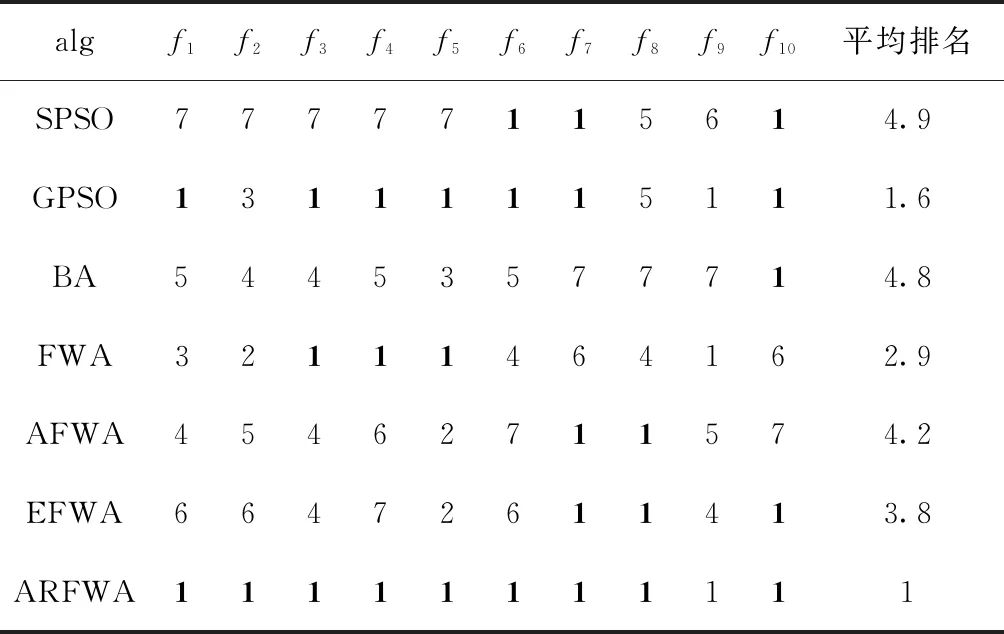
表3 在测试函数上的平均排名

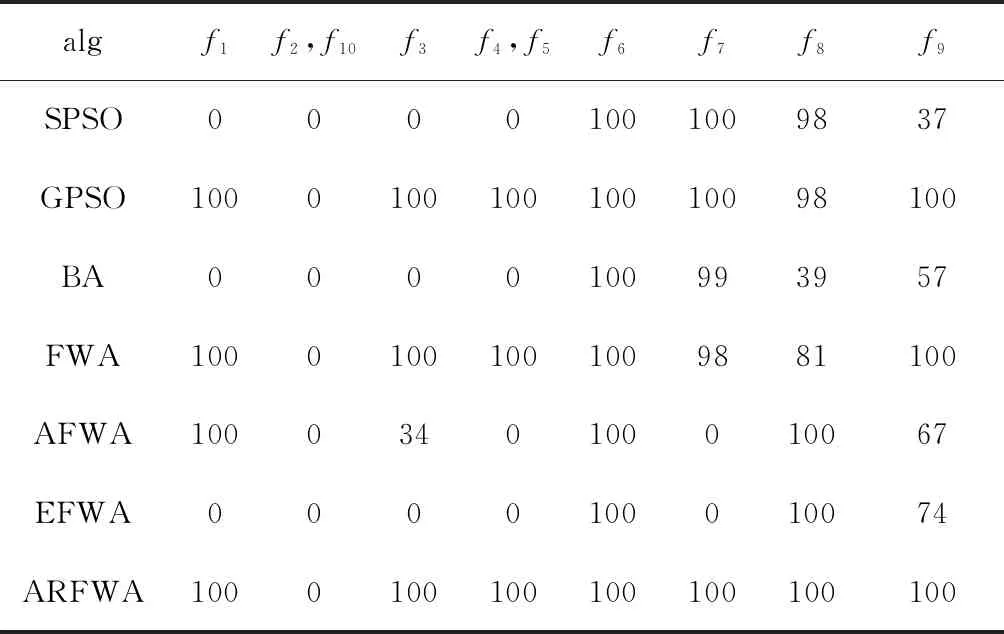
表4 f1～f10：7种算法寻优成功率SR/%

观察f1、f3、f4、f6和f9函数寻优进化曲线图(图1、图3、图4、图6和图9)可知，当算法迭代的次数是一样时，ARFWA表现出的收敛性能(收敛速度和收敛精度)明显比其它对比算法更出众。由表2对应函数的结果avg可得，ARFWA与GPSO具有一样的avg，且比其它对比算法更优。

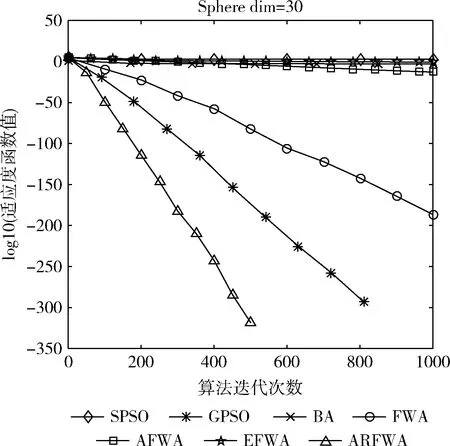
图1 f1寻优进化曲线

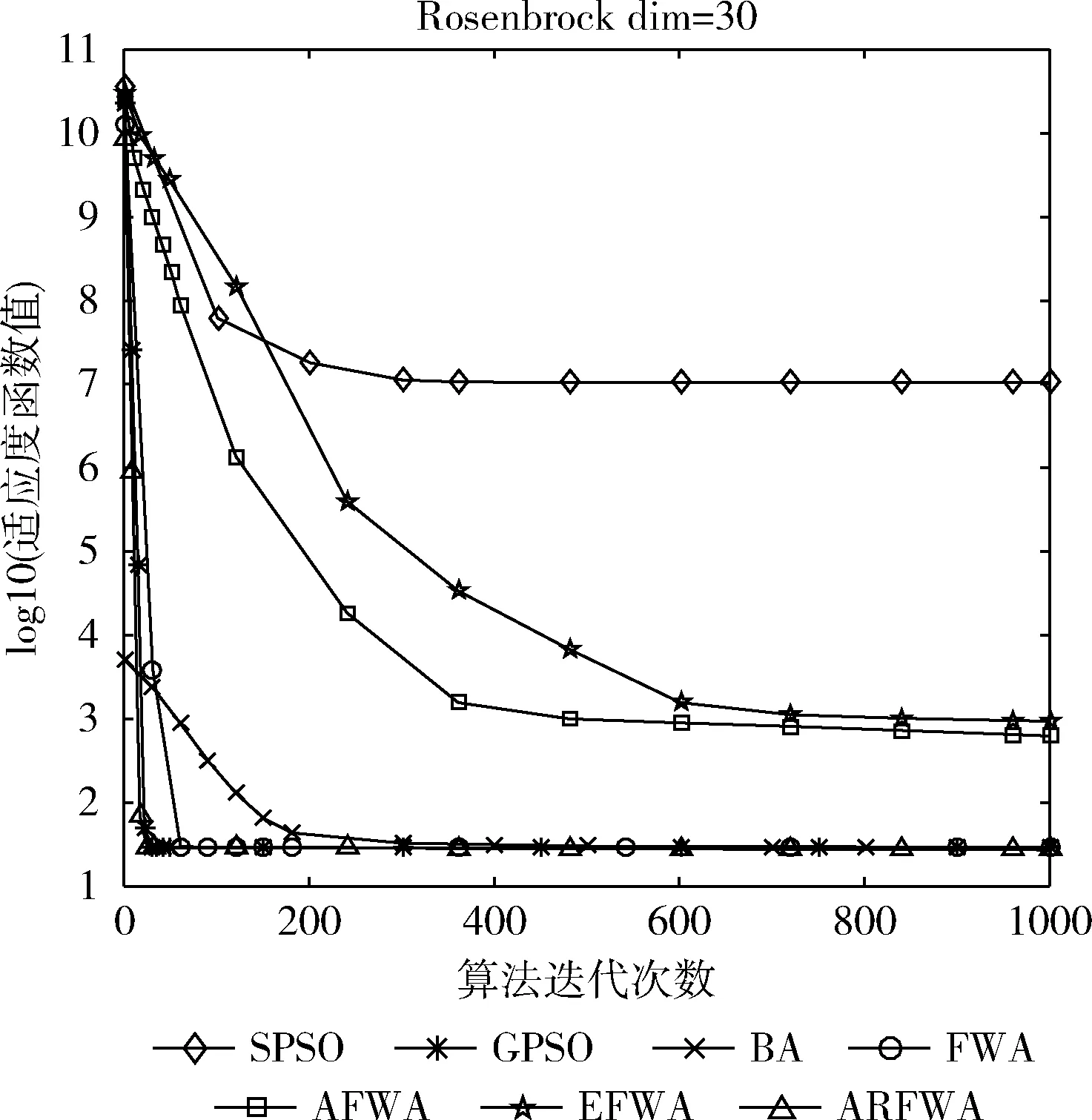
图2 f2寻优进化曲线

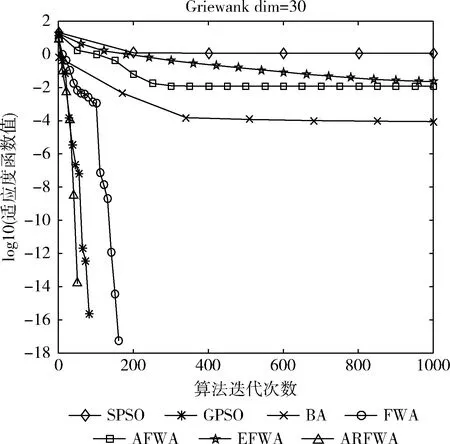
图3 f3寻优进化曲线

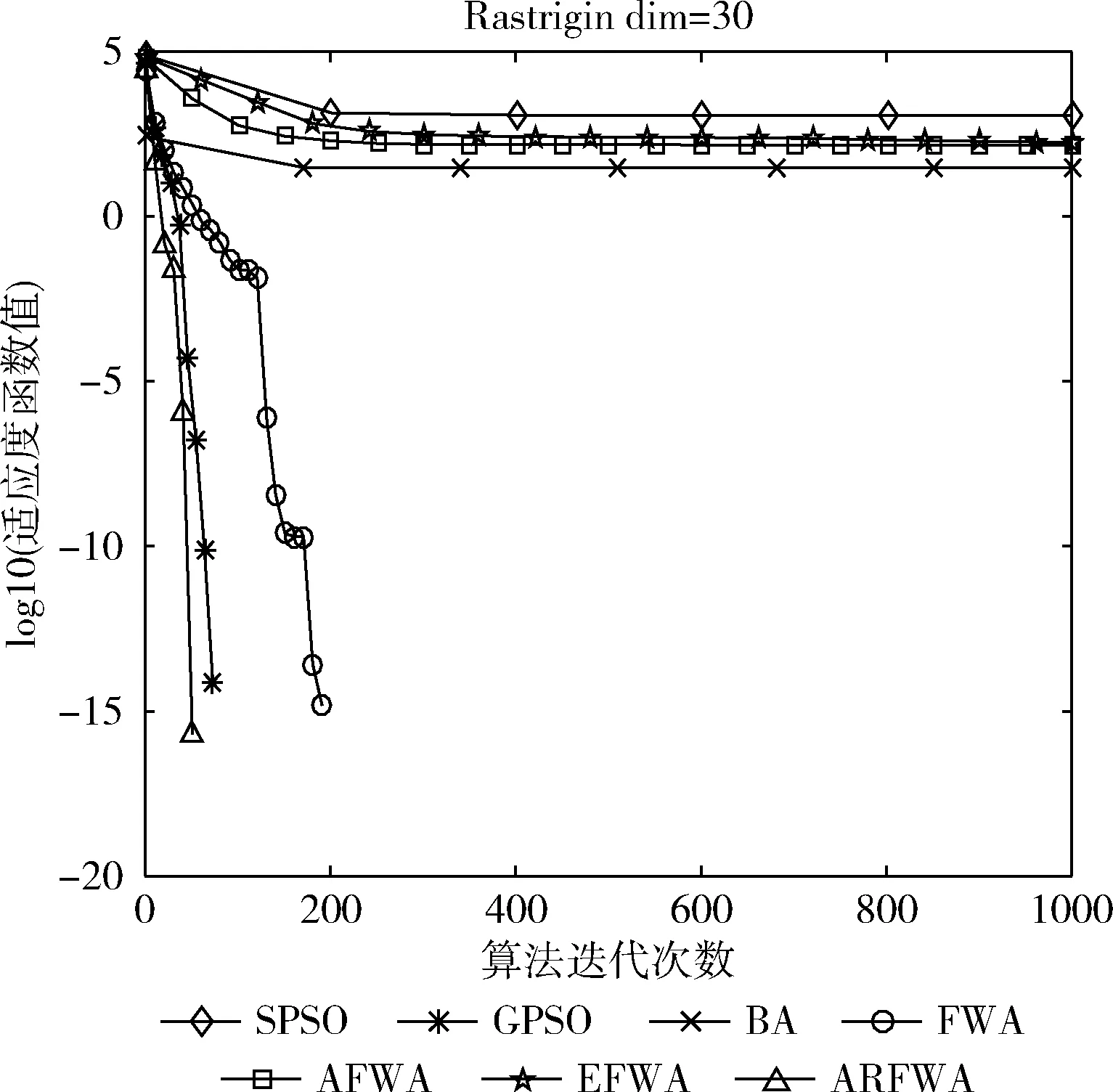
图4 f4寻优进化曲线

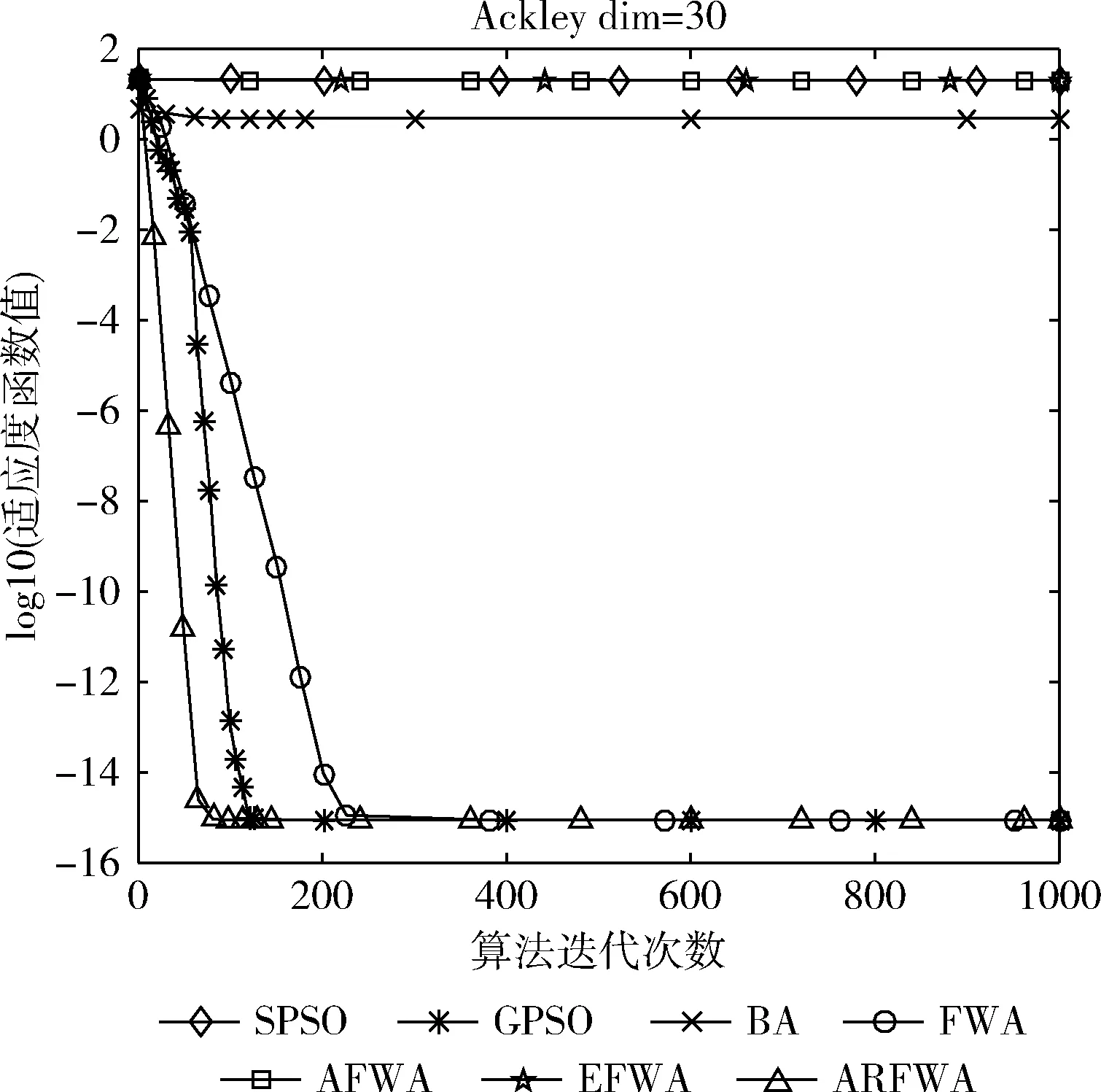
图5 f5寻优进化曲线

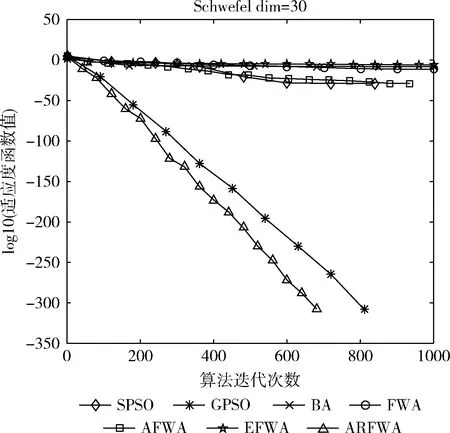
图6 f6寻优进化曲线

图7 f7寻优进化曲线

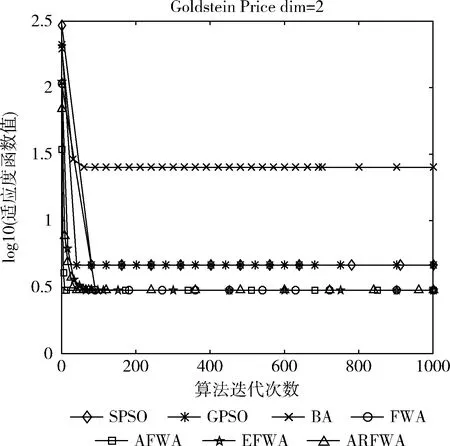
图8 f8寻优进化曲线

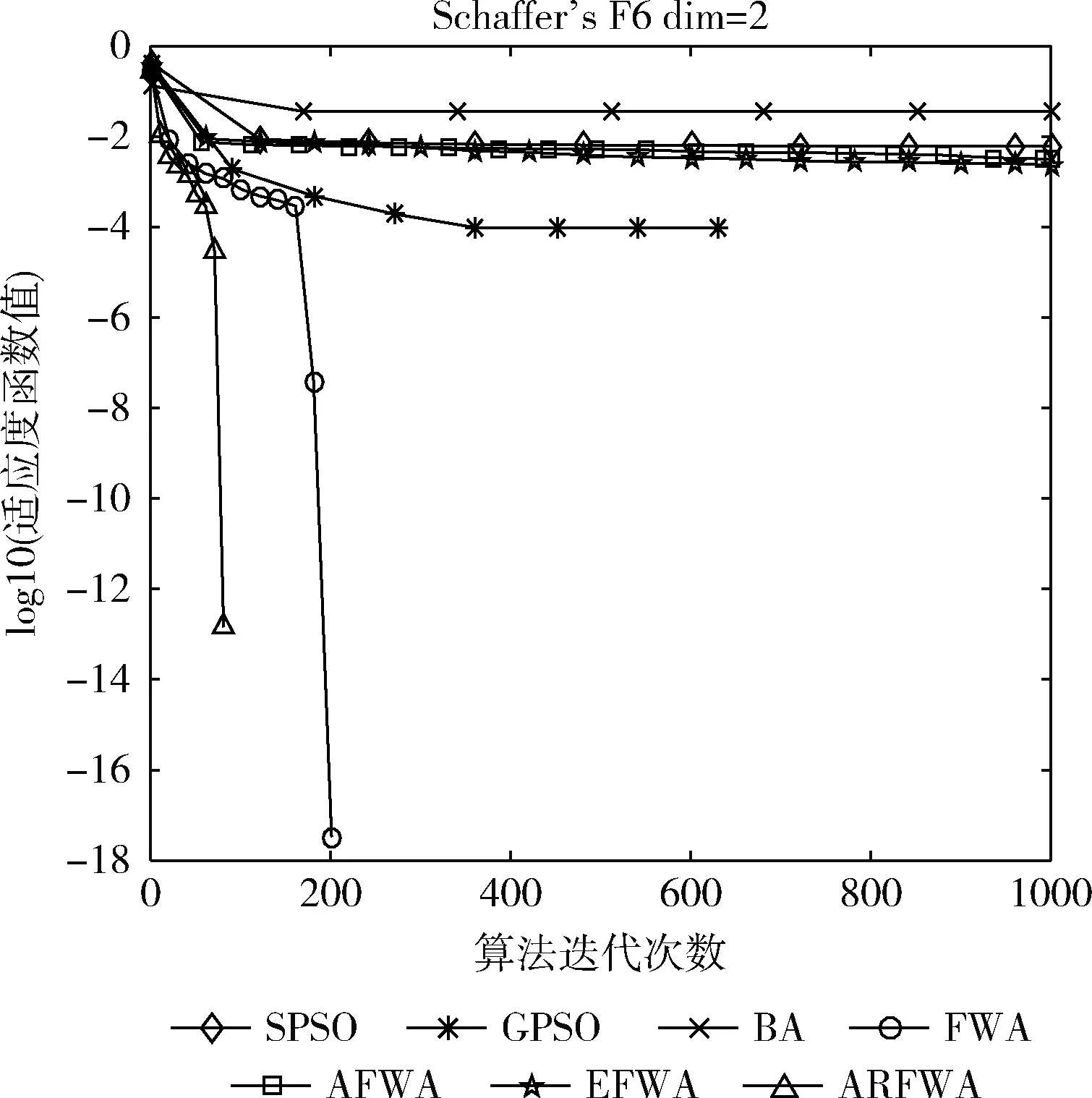
图9 f9寻优进化曲线

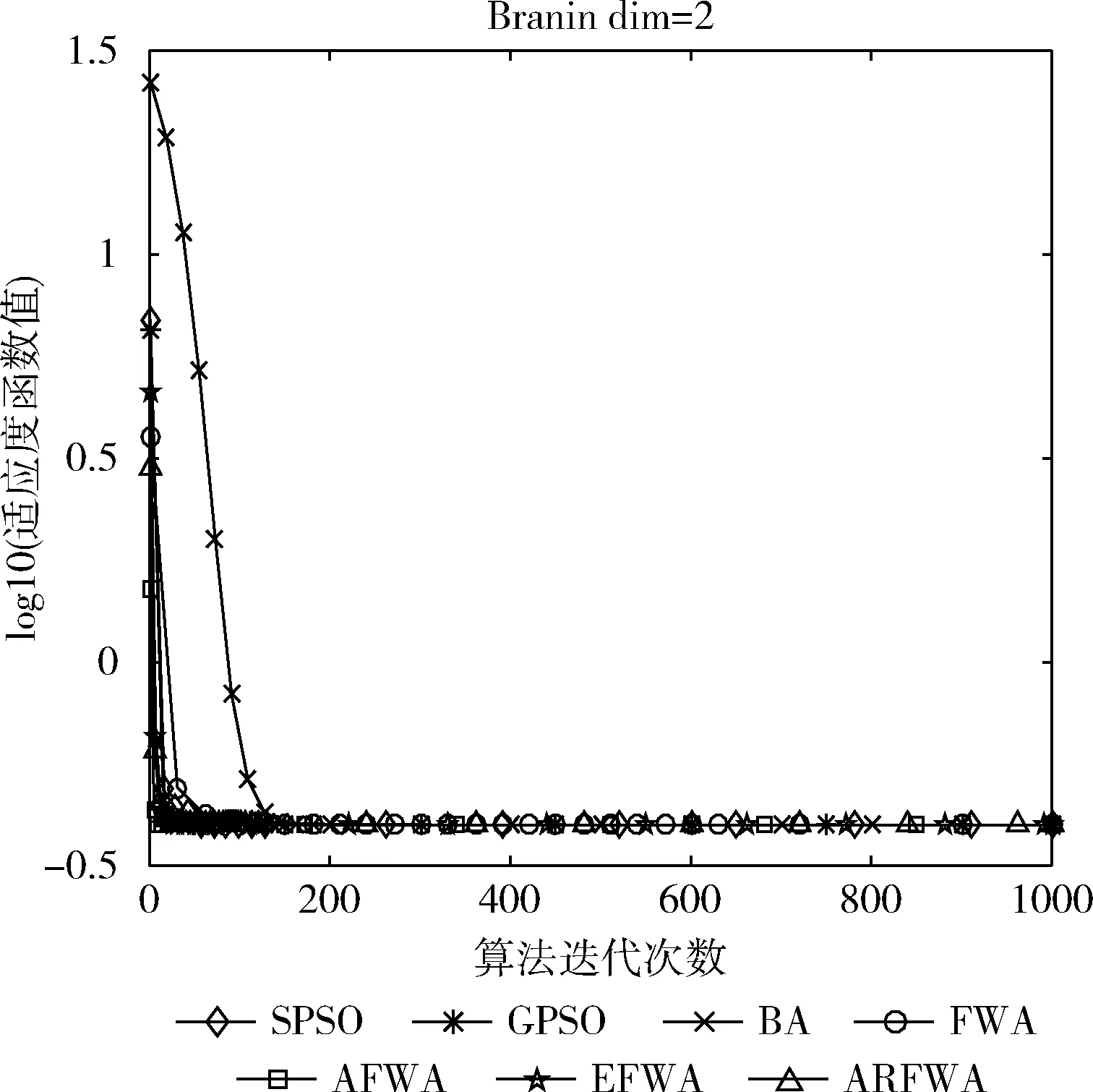
图10 f10寻优进化曲线

观察f2、f5函数寻优进化曲线图(图2和图5)可知，在算法迭代前期，迭代的次数一样时，ARFWA表现出的收敛性能(收敛速度和收敛精度)均比其它对比算法更优秀；但是在算法迭代后期，这7种算法均有“早熟”的情况，局部搜索能力没有很好发挥。由表2的f2函数的对应avg可得，ARFWA的avg比其它对比算法更优。由表2的f5函数的avg可得，ARFWA的搜索能力比AFWA算法略差，但是比其它对比算法更优秀。

观察f7函数寻优进化曲线图(图7)可知，当算法的迭代次数相等时，ARFWA呈现出的收敛性能(收敛速度和收敛精度)与其它对比算法相比实力相当，不分伯仲。由表2的f7的实验结果avg可知，ARFWA寻找到的平均解avg不亚于其它对比算法。

观察f8函数寻优进化曲线图(图8)可知，当算法的迭代次数相等时，ARFWA呈现出的收敛性能(收敛速度和收敛精度)稍差于AFWA，但是比其它对比算法更优秀。由表2的f8函数的结果avg可知，ARFWA、AFWA和EFWA求得的avg是一样的，但是比其它对比算法更优。

观察f10函数寻优进化曲线图(图10)可知，在寻优前期，当算法迭代次数相等时，ARFWA的收敛性能(收敛速度和收敛精度)稍差于AFWA，但是比其它对比算法突出；在算法寻优后期，7种算法均呈现出“早熟”的情况，局部搜索能力需要进一步提高。由表2的f10函数的avg可知，ARFWA求得的avg不亚于其它6种对比算法。

综上可知，ARFWA总体的收敛性能优于其它6种对比算法。

3.4 各算法在测试函数的平均排名

为了更直观看出各个算法的搜索能力，由表2的avg得到各算法在测试函数上的平均排名见表3，从表中可知，ARFWA在7种算法中排名第一，远远优于其它6种算法，即改进的烟花算法的整体搜索能力优于其它6种算法。

3.5 鲁棒性分析

鲁棒性的强弱可以通过标准偏差std的大小来判定。如果std越小，表示算法的鲁棒性越强；反之，其鲁棒性越弱。通过表2的实验结果，对于f1、f3、f4、f5和f9测试函数，ARFWA、FWA和GPSO表现出的实力相当的鲁棒性，且比其它4种对比算法更优秀；对于f2测试函数，ARFWA的鲁棒性比FWA和GPSO两种算法略弱，但是比其它4种对比算法更强；对于f6测试函数，ARFWA、SPSO和GPSO具有实力相当的鲁棒性，且比其它4种对比算法更强；对于f7测试函数，ARFWA的鲁棒性处于中等的实力，比SPSO、GPSO和AFWA这3种对比算法略弱，但比其它3种对比算法更强；在f8寻优过程中，ARFWA的鲁棒性稍逊于AFWA，但是优于其它5种算法；在f10寻优过程中，ARFWA的鲁棒性稍逊于SPSO、GPSO、EFWA，但优于其它3种算法。所以，综上可得，在10个基准函数寻优过程中，ARFWA的鲁棒性总体来说是比较好的。

3.6 寻优成功率分析

寻优成功一次是指在优化函数过程中，一次寻优的结果与理论最优值差值的绝对值不大于实验设置的精度。由表4得，在迭代结束时，ARFWA寻优成功率均为100%的有8个基准函数；GPSO寻优成功率均为100%的有7个基准函数；FWA寻优成功率为100%的有6个基准函数；AFWA寻优成功率均为100%的有3个基准函数；SPSO、EFWA寻优成功率均为100%的只有2个基准函数；BA寻优成功率为100%的只有1个基准函数。所以，整体而言，在10个基准函数的寻优过程中，ARFWA的寻优成功率比较好。

3.7 讨 论

通过实验对比分析可以知道，改进的烟花算法ARFWA的整体性能比其它6种对比算法的更优秀体现在如下几个方面：

(1)将粒子群算法的记忆机制引入改进的烟花算法中，借鉴了全局最优和个体最优的概念。本文引入sparkpBest来表示在寻优过程中每个烟花所产生的最优爆炸火花个体的集合以及gBest来表示全局最优烟花。当烟花的爆炸火花的数目大于或者等于平均爆炸火花的数目，说明该烟花向gBest学习，此时的烟花位于相对比较好的区域；反之，当烟花的爆炸火花数目小于平均爆炸火花数目时，说明烟花向sparkpBest学习，此时烟花处于相对比较差的区域；

(2)对全局最优gBest进行高斯扰动，以便增加种群的多样性，避免出现“早熟”的现象；

(3)构造了新的爆炸半径计算公式，标准的烟花算法对未被选择的爆炸火花全部丢弃，没有充分利用到被丢弃的爆炸火花的信息，而改进的烟花算法恰恰利用到这一点，将其充分利用，提高了烟花种群的信息利用率。

4 结束语

烟花算法是一种新颖的群智能算法，针对烟花算法后期收敛速度慢和求解精度不高的问题，充分利用了被舍弃的爆炸火花个体的信息，构造新的爆炸半径计算公式，以便能够自适应地调整步长；另外，在寻优的过程中，在原来高斯扰动的基础上，对全局最优个体进行高斯扰动，以此平衡局部和全局搜索能力，避免烟花种群过快陷入局部最优，增强收敛速度和收敛精度。由仿真实验可得：相对其它6种算法，整体而言，改进的烟花算法整体呈现出比较优秀的性能，表现在收敛性能方面(收敛速度更快、收敛精度更高)和鲁棒性更强。

在接下来的研究工作中，将对ARFWA算法进行进一步的优化，并将其应用于实际中。