求解约束优化问题改进的水波优化算法
顾启元,王俊祥
(重庆文理学院 软件工程学院,重庆 402160)
0 引 言
约束优化问题普遍存在于科学研究和工程领域中,通常这类优化问题含有多个线性、非线性约束条件,属于难处理的一类最优化问题[1]。不失其一般性,约束优化问题可描述为

(1)
式中:f(·)为目标函数,lk和uk分别为xk的下界和上界;gi(X)和hj(X)分别表示不等式约束和等式约束;如果存在集合R,R中元素可以使n个g(x)不等式和m个h(x) 等式成立,那么集合R中的元素视为一个可行解。
经典非线性规划方法求解约束优化问题前提条件是目标函数和约束条件连续且可微。群智能优化算法为非连续、多模态等复杂的约束优化问题提供求解新路径[2-5]。水波优化算法(water wave optimization,WWO)是一种新型群智能优化范式,由国内学者郑宇军提出[6]。WWO算法受浅水波理论模型启发,水波个体利用传播、折射和碎浪方式在解空间中有效搜索[7]。WWO算法具有原理简明、控制参数较少、易于实现等优点。目前WWO已在软件形式化开发关键部件选取[8]和车辆路径[9]等领域上取得了成功的应用。
WWO在求解无约束问题中已崭露头角[10-12],但是求解约束优化问题鲜有报道。本文尝试提出改进的WWO算法求解约束优化问题。首先设计了主从异构种群,即两个种群采用不同的更新方式,主群结合ε约束处理技术实现探索可行解,为了加快收敛速度和增强信息交互,主群中个体可以依概率进行个体间学习。在主群传播更新方式中,设计了关于水波适应度值和违反约束度的波长函数,利于水波个体根据进化状态及时调整波长。从群负责利用可行解搜索全局最优解,为了避免早期收敛,从群采用了自适应学习策略以平衡群体的探索和利用。最后设计了随迭代次数变化的放松约束度,不仅可以充分利用不可行解的信息以获得可行解,还可以提高算法收敛精度。实验结果表明,IWWO算法在求解约束问题方面展现出优越性。
1 标准WWO
WWO算法将待求问题的解空间比作为海床,每个水波类比为一个潜在解Xi。水波适应度被定义为关于水波与海平面垂直距离的函数:当水波越靠近海平面,则适应度越高[4]。WWO算法通过传播、碎浪和折射3个操作完成寻优过程。
1.1 传 播
水波通过传播操作完成运动过程,第i个水波Xi更新方程如下
(2)
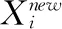
(3)
式中:μ为波长衰减系数;f(Xi)为个体Xi的适应度值;fmax和fmin分别表示当前群体中最大适应度和最小适应度值;为避免分母为零,设置为一个极小的正数。
1.2 碎 浪
为了对潜在最优解邻近区域实施精细搜索,对当前新的最优解进行碎浪操作。具体操作是先随机选择K维,被选择的每一维按式(4)产生一个孤立波为Xnew
(4)
式中:β是碎浪系数 (β∈(0.001,0.01));Xg表示当前种群获得的最优解;α为N(0,1)高斯随机数;K通常选取为min(12,D/2)[7](D是水波的总维度);如果产生所有的孤立波f(Xnew) 当水波的波高值递减为0时,该水波停止进化。为了改善水波停滞情况,水波算法按式(5)实施折射操作 (5) 式中:N(u,v) 为高斯随机数,其中u,v分别为均值和方差;Xg为当前群体最优解;水波Xi根据式(5)更新后,其波高h重置为最大值;其波长按式(6)更新 (6) IWWO采用异构主从种群结构进化,主群负责在搜索范围内寻找可行解,从群负责接收主群传递的可行解,并利用可行解进一步寻优,提高可行解的质量。 2.1.1 主种群更新策略 为了增强信息交互加快收敛速度,主种群中水波依概率学习群体中其它个体。主种群中的水波按式(7)更新 (7) 式中:j∈(1,2,…,N)(N为种群规模);rand(0,1) 是服从[0,1]均匀分布的随机数;水波个体依概率η实施传播操作,依概率1-η学习其它个体。η为学习率,其值随迭代次数变化,按式(8)更新 η=(T-ηmin·t)/T (8) 式中:t为迭代步数,T为最大迭代步数;ηmin为最小学习率。随着迭代次数增加,η值由1递减为ηmin,使得水波个体在进化前期依较大概率进行个体间的相互学习,充分利用优秀个体的信息快速找到可行解;在进化后期,水波个体依较大概率实施传播操作,利于全局勘探可行解。 在标准WWO中,水波波长是由水波的适应度值、种群中最大适应度值和种群中最小适应度值确定的。但是在约束问题中,对水波个体的评价不仅仅依赖适应度值,还需考虑该水波是否是可行解,水波波长只随适应度值而变化是不合适的。因此,设计了关于适应度值和约束违反度的水波波长函数,该函数根据水波进化状态及时调整水波波长 (9) 式中:φ(X)称为约束违反度,是对违反约束的度量;通过式(9) 可知,当φ(X)为零时(即水波为可行解),波长的变化与该水波的适应度值有关;当φ(X)不为零时(即水波为不可行解),为了防止水波波长下降过快,波长的变化是关于该水波适应度值和约束违反度的函数,φ(X)按式(10)计算[13] (10) 式中的不等式条件G(X)按式(11)计算 (11) 难以精确地处理等式约束问题,一般将等式约束转化为满足一定精度的不等式约束来处理。所以,式(10)中的H(X)按式(12)计算 (12) 式中:δ为等式约束的容忍参数(通常取值δ=10-4)。 β=(βmaxT-βmin·t)/T (13) 其中,βmin、βmax分别为碎浪系数的最小值和最大值。 2.1.2 从种群更新策略 从种群采用自适应的折射算子,主要用于对可行解的局部利用,更新方程如下式 (14) w=1-t/2T (15) 解决约束优化问题,如何处理约束是获得最优解的关键,ε约束技术对扩大搜索空间具有良好效果。通过违反度阈值ε调节不可行解和可行解的关系[13]。当0<(X)<ε,水波个体处于不可行解区域,称X为优秀不可行解。 按照下列准则评价水波个体的优劣: 准则1水波个体Xi和Xj均为可行解时,如果适应度值f(Xi)>f(Xj),则Xi占优Xj; 准则2水波个体Xi和Xj均为不可行解时,如果约束违反度φ(Xi)<φ(Xj),则Xi占优Xj; 准则3水波个体Xi和Xj,令Xi为可行解,Xj为不可行解。若Xj是优秀不可行解,则Xi和Xj中适应度值高的个体占优;若Xj不是优秀不可行解,则可行解Xi占优。 ε约束处理技术中合适的约束违反度阈值ε利于算法的收敛性。新算法中设计一个自适应ε,其值随着迭代次数自动调节的ε松弛度,不仅可以有效利用不可行解的信息提高解质量,而且可以帮助提高收敛速度 (16) 式中:t为迭代步数,T为最大迭代步数。由式(16)可知,松弛度ε从ε0开始递减,在进化初期松弛度有较大的值,提高利用可行域的效率;后期松弛度为0,利于算法及时收敛。 IWWO算法求解约束优化问题的流程如算法1所示。 Algorithm 1:IWWO Input:待求解问题参数设置(包括问题维度D、迭代总次数T、种群规模N、约束条件适φ(·)、适应度函数f(X) 等) Output:种群最优解Xg 步骤1 参数实施初始化,在解空间内随机初始化主群和从群,计算每个水波的适应度f(X)和约束违反度φ(X); 步骤3 对主群的每个水波Xi实施如下操作: 司马迁对“至圣”孔子之关注,是出于继承孔子“作《春秋》”伟大事业的遗志,也是出于对孔子的情感认同。那么司马迁心中的“至圣”又有着什么样的内涵?他笔下的“至圣”孔子又有怎样的特点? 步骤4 若主群更新完毕,则转向步骤5,否则返回步骤3; 步骤5 对子群的每个水波Xi实施如下操作: 为了测试本文算法在求解约束问题的优化性能,选取参考文献[2-4]中24个标准函数,这些测试函数被广泛用于测试求解约束优化问题的算法。 第一组实验设计为了测试算法中改进的策略对求解性能的影响。选取10个测试函数((g01-g10))。对比的算法有标准WWO(SWWO),SWWO1和IWWO算法,其中SWWO算法采用固定ε值的约束处理技术;SWWO1算法采用文中提出的自适应ε约束处理技术和改进的波长更新策略;为了保证实验的公平性,设置算法的迭代次数为2×104;所有算法独立运行25次。算法的具体参数设置见表1。 表1 3种水波算法参数设置 表2列出了SWWO、SWWO1和IWWO这3种算法求解10个约束问题的实验结果。表中函数名所在的列给出了每个函数名和每个函数已知最优解;表中给出了25次迭代获得的最优解的均值(Mean)、标准差(Std)及依据均值对算法的排名(Rank),其中用粗体表示算法比较中获得最优的结果。 从表2的结果中可以看出,3种算法中IWWO算法获得优化性能最好,SWWO1优化性能次之,SWWO优化性能最差。与SWWO相比,SWWO1在10个问题上的优化性能都有所提高,特别在g05, g07~g10 5个函数上,SWWO1性能有明显提高。说明改进的波长更新策略和自适应的ε约束处理技术有助于提高解的质量。 表2 3种水波算法获得的实验结果 IWWO算法在g01,g03,g04,g05,g06,g08和g09这7个函数上找到已知最优解,说明IWWO具有良好的优化性能。与SWWO1相比可知,IWWO在10个函数的优化性能都得到较大的提高。SWWO1和IWWO算法中采用了相同的改进波长更新策略和自适应ε约束处理技术,IWWO获得更优越的性能是因为IWWO采用了异构主从的种群结构和相应的更新策略。第一组实验结果表明了文中提出的异构主从的种群结构、波长更新策略和自适应ε约束处理技术对提高解质量是有效的。 第二组实验设计是将最新求解约束问题的算法与本文算法进行对比分析。对比算法有混沌灰狼算法CGWO(2018)[2],基于E-BRM遗传算法(2018)[3]和改进的全局人工蜂群算法MGABC(2018)[4]。算法独立运行25次,最大迭代次数是2×104,种群规模为100;CGWO的实验参数设置参照文献[2]。 实验结果见表3,表中基于E-BRM遗传算法的实验结果来自文献[3];改进的全局人工蜂群算法MGABC实验结果来自文献[4];表中‘-’符号表示文献没有提供该函数的实验数据;‘NF’符号表示没有找到可行解;对于每个函数,算法获得的最优的均值和标准差加粗表示。 从表3可知,对于cec2006的24个测试函数,IWWO算法能够稳定找到已知最优解的函数共12个(g01,g03,g04,g05,g06,g08,g11,g12,g13,g15,g16,g24),说明IWWO求解约束问题具有优良的寻优能力和鲁棒性。对于函数g17,目前已获得的最优解8853.5397,IWWO获得最优解为8853.5371,优于当前最优解。对于g20(问题维度为22)和g22(问题维度为24)两个高维函数,IWWO可以找到可行解,但是E-BRM和 CGWO算法并没有找到可行解。表明对于高维复杂约束优化问题,IWWO也具有良好的寻优潜力。 表3 24种求解约束优化算法对比实验结果 表3(续) 对于g02函数,IWWO排名为第4;对于g10和g18函数,IWWO排名为第2;在其它17个函数上,IWWO排名均为第一。CGWO在g10函数排名第1;E-BRM在g02,g08,g12和g24这4个函数上排名第一;MGABC在 g08,g12,g16,g18和g24这5个函数上排名第一;按平均排名,IWWO得分是1.25,MGABC得分是2.15,E-BRM得分是2.29,CGWO得分是3.08。由平均排名可知,IWWO的优化性能最好,MGABC优化性能次之,CGWO优化性能最差。 本文提出一种改进的水波优化算法求解约束优化问题。算法中设计了自适应ε约束处理技术充分利用不可行解信息,增加可行解个体规模;设计了主-从异构种群,以平衡群体的探索和利用。设计了水波波长函数,使其随着水波的适应度值和违反约束度及时调整。与其它算法比较结果表明本文提出的算法在求解带有等式约束和不等式约束的优化问题时展现了良好的整体优化性能。 从实验结果分析可知,针对高维约束优化问题,虽然本文的提出算法可以找到可行解,但是可行解的精度有待进一步提高。下一步工作,将通过与其它技术结合的方法提升高维约束优化问题解的质量。1.3 折 射
2 IWWO求解约束优化问题
2.1 IWWO
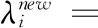
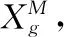
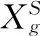
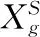
2.2 约束条件处理
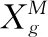
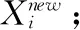
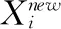
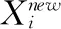
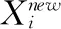

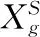
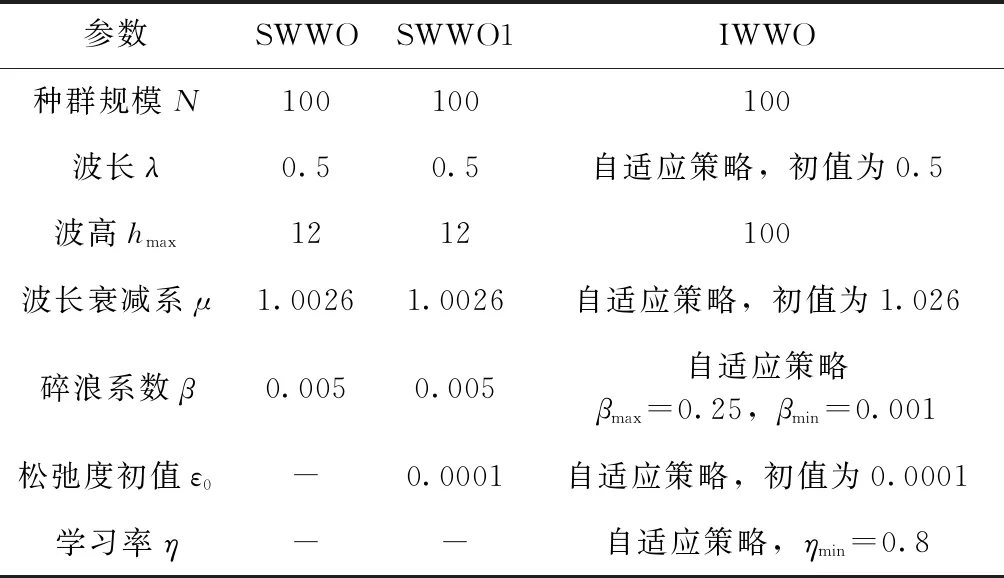
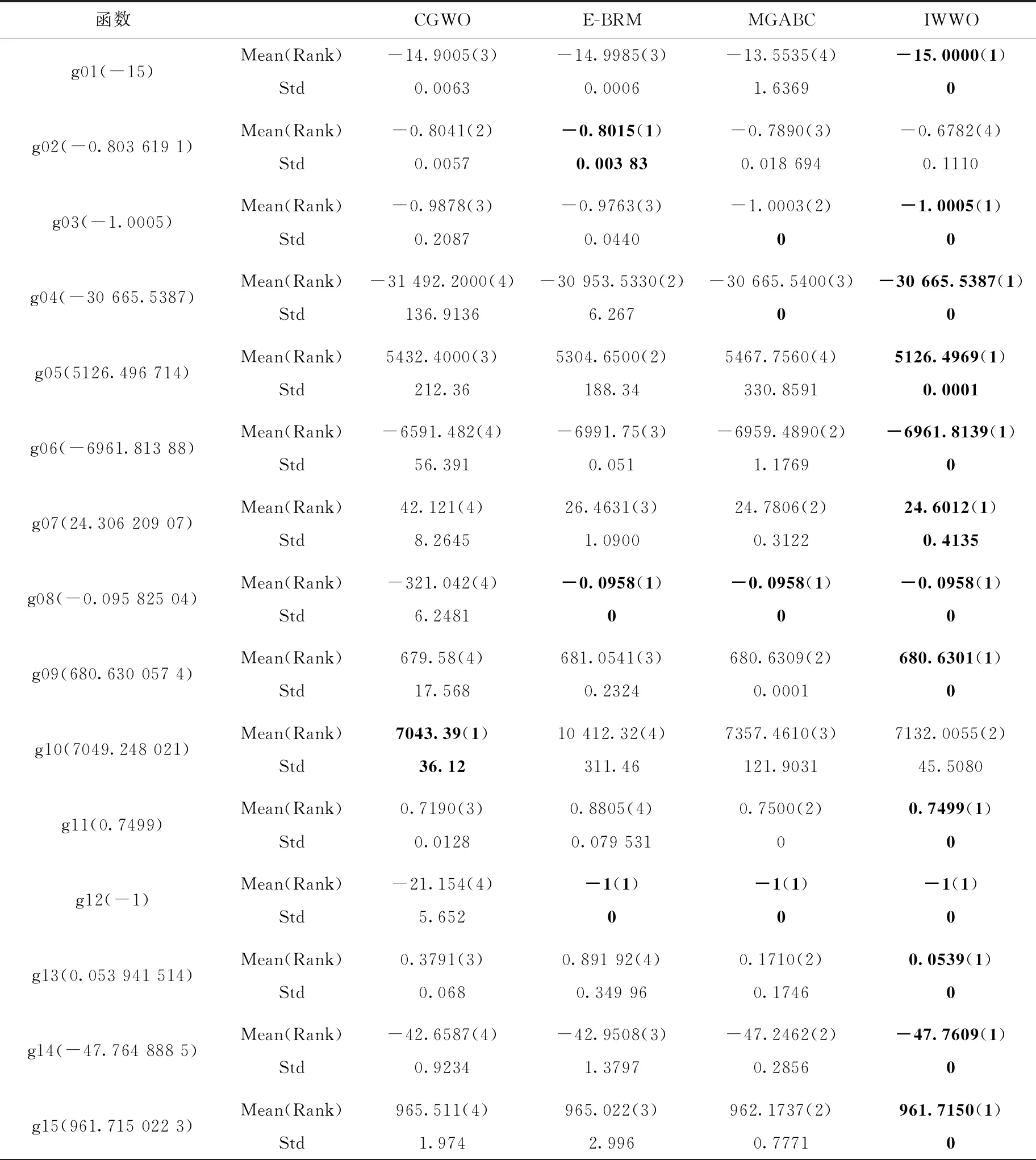
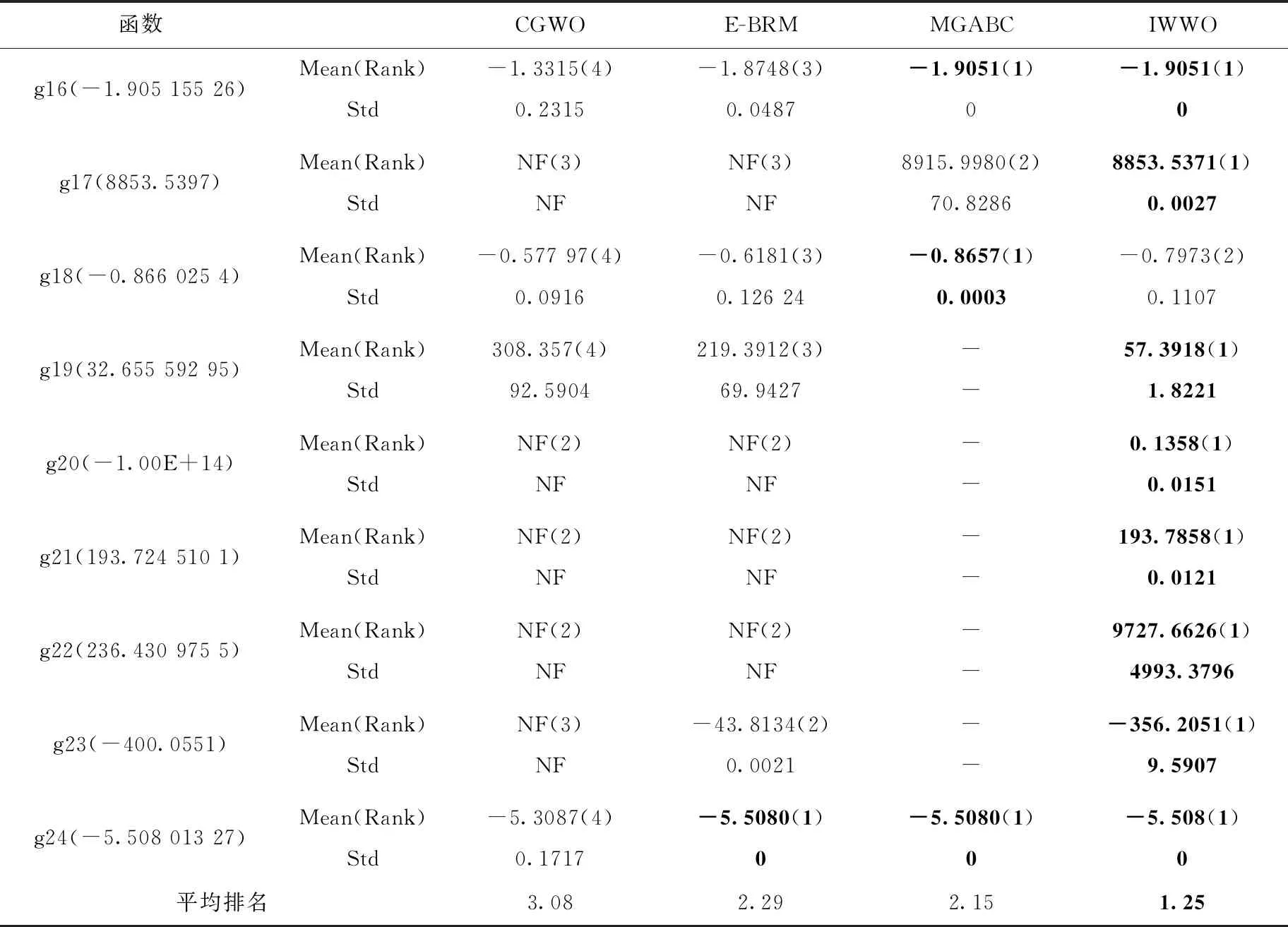
3 数值实验

4 结束语

