基于HDBACAN聚类的自适应过采样技术
董宏成,赵学华,赵 成,刘 颖,解如风
(1.重庆邮电大学 通信与信息工程学院,重庆 400065;2.重庆市质量和标准化研究院,重庆 400023;3.重庆信科设计有限公司,重庆 401121)
0 引 言
近年来有很多旨在改善不平衡学习问题[1-5]的研究,如随机过采样Random Oversampling[6]是随机复制少数类样本使类分布达到平衡,该方法可有效提高分类器的分类性能,但容易导致过拟合。José等提出了一种改进型的SMOTE过采样方法[7],该方法简单有效但其合成样本机制是盲目的。Annisa等采用一种改进型的自适应过采样方法ADNSYN[8]来重新平衡数据集。该算法虽然可有效提升分类器的分类性能,但忽略了类内不平衡问题。为了解决类内不平衡,Georgios等[9]提出一种K-SMOTE算法,该算法采用K-means聚类方法先对整个输入空间进行聚类,然后对过滤的集群进行随机过采样。该方法可同时解决类间和类内不平衡问题,但其无法加强分类器对一些重要少数类样本的学习。
综上所述,虽然大多数算法都能克服现有过采样算法的一些缺点,但很少有算法能够避免产生噪声并同时减轻类间和类内不平衡问题。此外,许多技术都是比较盲目地合成新的样本,并不能根据数据的分布特征进行合理的抽样处理。因此,本文提出一种自适应过采样方法HD-SMOTE,该方法旨在更加合理地解决不平衡数据中的噪声、内类和类间不平衡等问题。
1 HDBSCAN聚类和SMOTE过采样算法
1.1 HDBSCAN聚类
HDBSCAN[10]是由Campello等开发的一种基于密度的聚类算法,它是DBSCAN聚类方法的一种变体。该算法会执行不同半径Eps值的DBSCAN,并集成所有结果以找到最佳的聚类解决方案。在聚类过程中,HDBSCAN首先根据密度对数据空间进行变换,求出所有样本点的最小生成树,然后对变换后的空间进行单连锁聚类。HDBSCAN不以单个Eps值作为树状图的分割线,而是在不同高度对树进行切割,根据集群的稳定性选择不同密度的集群。
HDBSCAN聚类方法相比K-means、均值漂移、层次聚类、DBSCAN等聚类方法有以下几点优势:①可以发现任意形状和不同密度的集群;②不用预先知道数据集的聚类数量和聚类中心;③对用户所设定的参数不敏感,其主要涉及的参数是min_cluster_size(集群的最小数量)和min_samples(集群中样本的最小数量);④可以为每个样本分配一个0.0到1.0的集群成员隶属度,若样本点的隶属度为0.0表示该点为离群点或者噪声样本,而隶属度为1.0则表示集群中心的样本。
1.2 SMOTE过采样方法
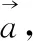
(1)
但是,在很多情况下,基于k-NN的方法可能会产生错误的少数类样本,为了说明原因考虑图1合成样本的情况。
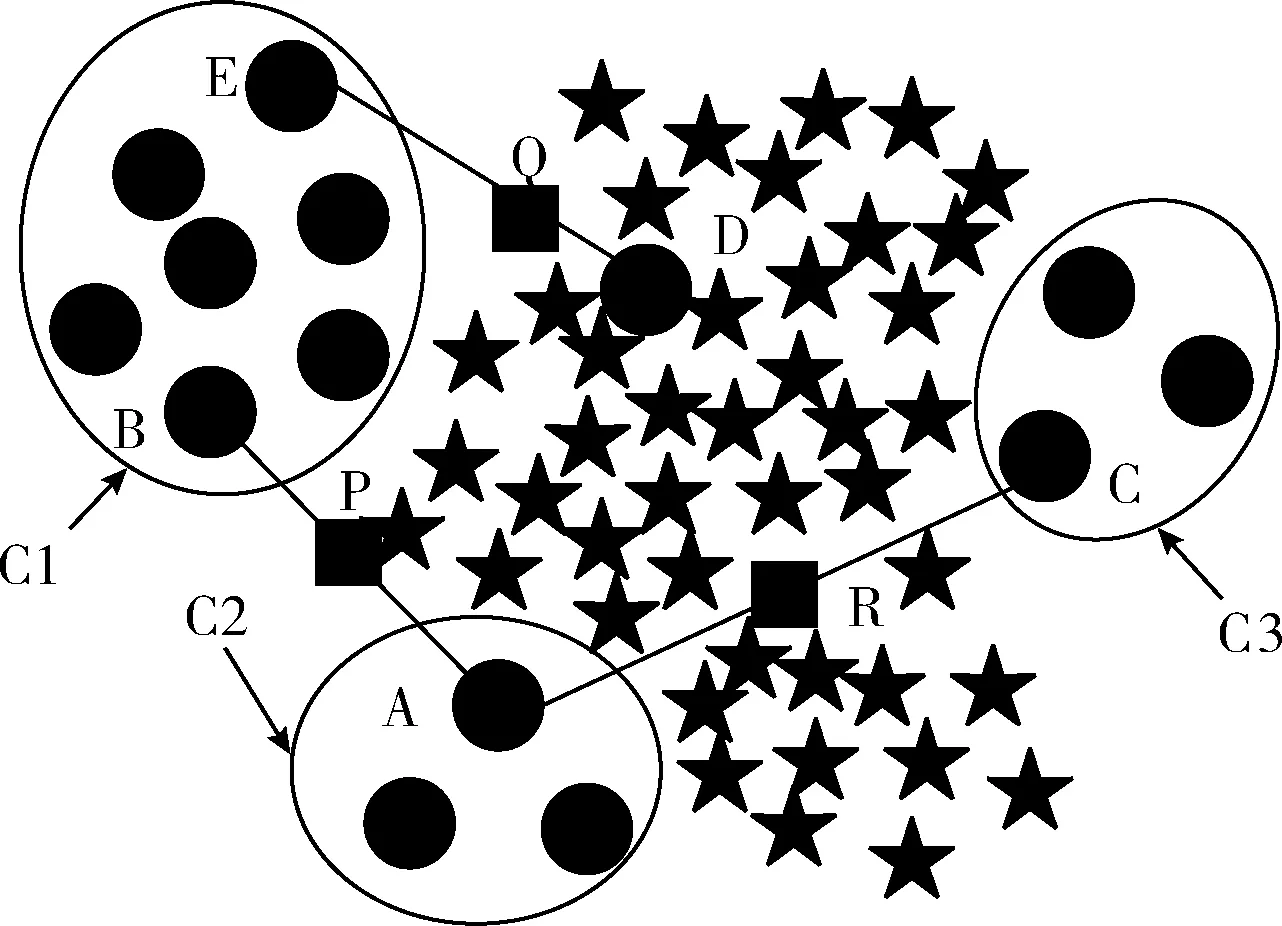
图1 类内不平衡下SMOTE合成样本
图1展示了在类内不平衡和小分离(缺乏代表样本,如集群C2)的情况下,SMOTE过采样技术合成样本的示意图,其中星型表示多数类样本,圆型表示少数类样本。这里假设样本A被选中且参数k=5,在A的5个少数类最近邻中样本B被选中,根据式(1)在样本A和B之间插值合成新的样本P。从图中明显可以看出,样本P是一个错误的样本,因为该样本和多数类样本重叠。若少数类样本中出现小规模的集群时,上述问题将被放大。如果集群C2中的一个样本被选中而该样本的一个近邻样本C(样本C分布在集群C3中)被选中,这时合成的样本R将分布在多数类样本中,这会使学习变得困难。若噪声样本D被选中用来合成样本,这种情况下将合成样本Q,若样本Q位于多数类区域将加大分类器的学习难度。SMOTE方法虽然可以有效地解决类之间的不平衡问题,但是类内部的不平衡、小分离物、噪声等问题都被忽略了。由于该方法选择的样本是随机的,这可能使样本空间中比较密集的区域中的样本进一步增多如集群C1,而比较稀疏的区域可能仍然保持稀疏如集群C2和C3。在这种情况下会放大不平衡数据的类内不平衡问题,增加分类器的学习难度。
2 HD-SMOTE自适应过采样算法
2.1 HD-SMOTE框架
为了克服1.2节中所探讨的SMOTE过采样方法的诸多缺陷,本文提出一种基于HDBSCAN聚类和SMOTE的HD-SMOTE过采样算法,HD-SMOTE算法框架如图2所示。首先利用HDBSCAN聚类算法对所有少数类样本D+进行聚类,得到m个互不相交且不同规模的集群cm和噪声集群N,这些噪声样本在下一步将被删除。随后HD-SMOTE算法根据每个集群cm的稀疏度合成新的样本,在稀疏度越高的集群合成更多的少数类样本,相应地在密集集群中合成较少的样本,以此克服数据的类内不平衡和小分离问题。在合成样本时,会选择集群中隶属度高的样本进行插值合成新的样本,这样合成的样本会靠近每个集群中心,可以保证新的样本点在安全区域合成,避免噪声的产生。
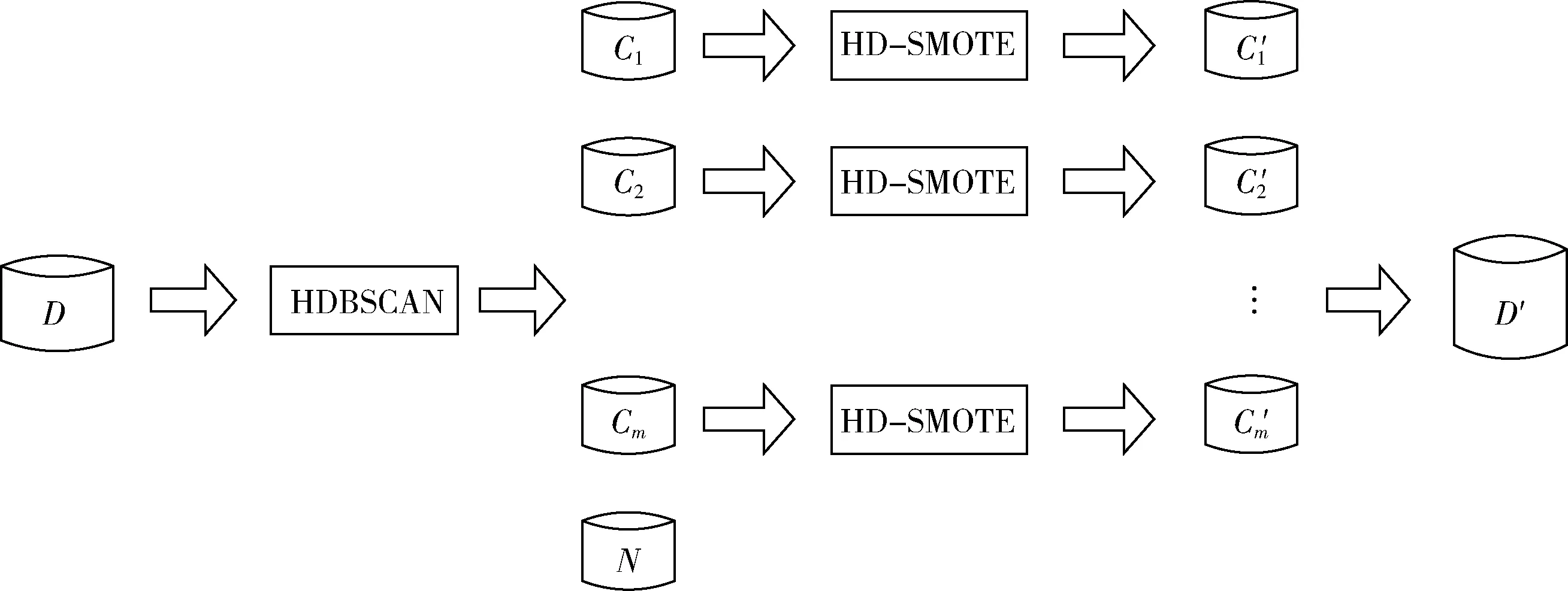
图2 HD-SMOTE过采样框架
2.2 改进的SMOTE过采样方法
为了确定每个集群需要合成的样本数量,给每个集群分配一个0到1之间的采样权重。采样权重越高的表示集群越稀疏,相应的集群合成的样本数更多;采样权重越小的表示集群越稠密,相应的集群合成较少的样本。为了确定每个集群的采样权重与合成的样本数目可以根据下面的步骤进行计算。
步骤1 对于每个集群f的欧式距离矩阵
(2)
其中,Dk为每个少数类集群ck的欧式距离矩阵,1≤k≤m,dij表示集群中少数类样本xi到xj的欧式距离。
步骤2 计算每个集群ck的平均距离
(3)
其中,n为每个集群的样本总个数,这里只需要用到距离矩阵Dk中的下对角线元素,因为dij和dji表示的距离是一样的。
步骤3 计算每个集群ck的稀疏度
(4)
n为集群的总样本数,从式(4)中可以发现,若集群的平均距离越小(集群中样本越密集),其对应的稀疏度就越小,反之则越大。
步骤4 计算所有集群的稀疏度之和Sparsitysum
(5)
其中,numf表示集群的数量。
步骤5 计算每个集群的采样权重
(6)
从式(6)中可以发现,若集群的稀疏度越大其采样权重越大。
步骤6 计算要合成的样本总数
N=Nmaj-Nmin
(7)
其中,Nmaj为多数类样本数,Nmin为少数类样本数。
步骤7 计算每个集群要合成的样本数
Samples(ck)=N×Sampleweight(ck)
(8)
2.3 HD-SMOTE的算法描述
假设整个训练数据集为T,少数类集合为P,多数类集合为N,P={p1,p2,…,ppnum},N={n1,n2,…nnnum},其中pnum和nnum分别是少数类样本数量和多数类样本数量。整个算法的流程主要分为4个阶段,具体步骤如下:
步骤1 识别少数类中不同规模的集群。
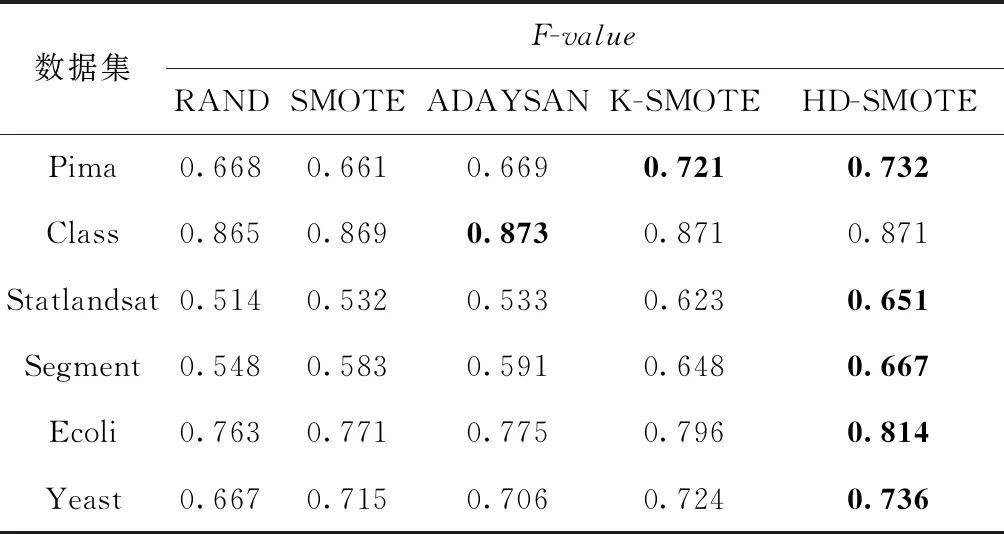
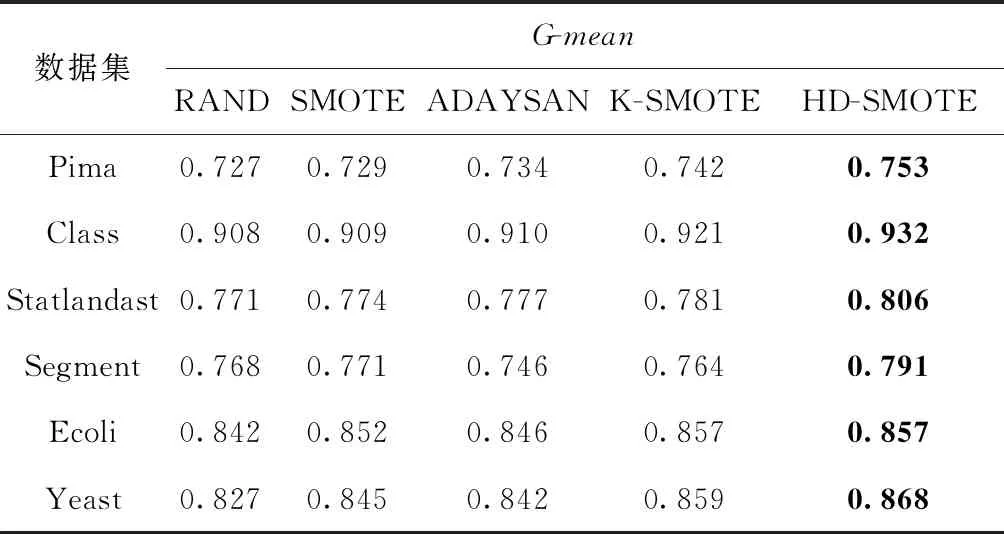
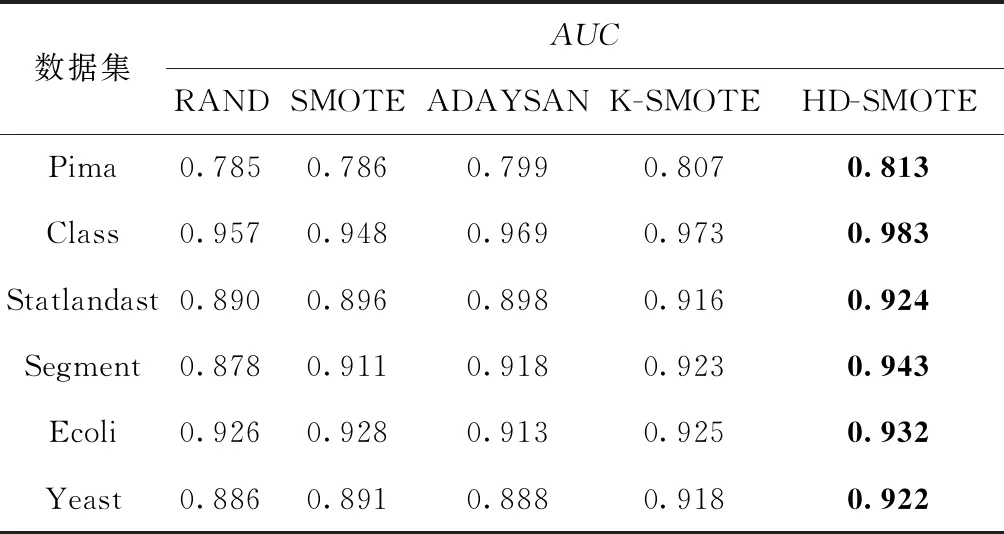
(1)HDBCAN对数据集P进行聚类,得到不同规模的集群c1,c2,…,cm和噪声集群N,并且得到每个集群的成员隶属度矩阵wij,0 (2)删除噪声集群N,计算剩余少数类样本总数,Nmin=pnum-|N|。 步骤2 计算每个集群需要合成的样本数Samples(ck)。 (1)遍历所有的集群c1,c2,…,cm,根据式(2)、式(3)、式(4)计算出每个集群的稀疏度Sparsity(ck)。 (2)根据式(4)、式(5)计算所有集群的稀疏度之和Sparsitysum。 (3)根据式(6)计算每个集群ck的采样权重Samplingweight(ck)。 (4)根据式(7)、式(8)计算每个集群ck需要的合成的样本数Samples(ck)。 步骤3 自适应地合成新的样本。 (2)输出c′k,返回上一步执行直到遍历完所有的集群,最终得到集合c′1,c′2,…,c′m。 步骤4 训练分类器。 (1)少数类集合c′1,c′2,…,c′m与多数类N组成训练集,利用这个训练集对K-NN分类器进行训练。 (2)利用测试数据集对分类器进行测试。 分类器的性能指标通常由一个混淆矩阵来评估,见表1。表1中行表示实际的类,列表示检测到的类。TP表示分类正确的少数类样本的数量;FN表示分类错误的少数类样本数量;FP表示分类错误的多数类样本的数量;TN表示分类正确的多数类样本数量 Recall=TP/(TP+FN) (9) Precision=TP/(TP+FP) (10) 表1 查全率、查准率中的参数意义 (11) TNR=TN/(FP+TN) (12) TPR=TP/(TP+FN) (13) FPR=FP/(TN+FP) (14) (15) Recall(查全率)表示在所有少数类的样本中被正确分类的样本所占的比率;Precision(查准率)表示在所有被分类器分为少数类的样本中正确分类样本所占的比率;F-value可以衡量分类器对少数类样本的每个指标性能,F-value越大表示分类器对少数类的识别精度越高。G-mean是评价分类器整体性能的一个很好的指标,因为它结合了分类器对少数类和多数类的精度。另一个非常流行的测量方法是接收机工作特性(ROC)图的下面积,通常称为AUC[11]。与G-mean和F-value测量度不同,AUC对多数类和少数类样本的分布不敏感,适合测量分类器对样本分布不均匀的性能。通过在x轴上绘制假阳性率(FPR)和在y轴上绘制真阳性率(TPR),通过计算得到的ROC曲线图的下面积便是AUC值。当AUC=0.5时表示分类器相当于一个随机猜测的分类器,AUC=1时表示分类器对所有样本的分类准确率为百分之百。AUC值越大表示分类的综合效果越好。 本文的实验选取了来自机器学习数据库UCI[12]Class,Statlandast,Segment,Ecoli和Yeast数据库。表2中的列分别表示数据集名称(Name)、少数类(MinorityClass),样本数量(Instance)、少数类样本数量(Min)、多数类样本数量(Man)和不平衡比(Ibr)。对于每个数据集,目标类为少数类,其余类被合并创建为多数类。 表2 实验数据的特征与分布 为验证本文所提过采样方法的有效性,HD-SMOTE算法分别与Random Oversampling、SMOTE和ADASYAN这3个使用最广泛的算法进行对比,并且和一个最新的 K-SMOTE 算法进行对比。本文中的算法用到的 HDBSCAN 的聚类算法可以在Python库Scikit-learn[13]调用。 HDBSCAN中的参数设置为min_cluster_size=2,min_samples=3。 分别表示HDBSCAN对少数类样本进行聚类所得到的集群的数量至少有两个,每个集群中所包含样本数量至少有3个。本文中其它对比算法所涉及的SMOTE算法的参数k均设置为5(默认值),k近邻分类器的参数K也设置为5。其中新算法K-SMOTE中用到的K-means聚类算法的参数k∈{2,5,10,20,50},最终本文中只列出该算法在各个数据集中不同k值下分类效果最好的实验数据。实验中各个算法获得的F-value值、G-mean值和AUC值均是采用5倍交叉取平均值得到的。 表3列出了5种算法分别在6个数据集上的F-value值,表中黑色加粗的数字表示该行的最大数值。从表中可以发现HD-SMOTE算法在其中5个数据集上获得的F-value值最高,该算法在Yeast数据上的F-value值提升最高,相比RAND算法的F-value值提升了6.9%。这是质的提升,因为F-value值是衡量分类器对整个少数类的分类精确度,对查全率和查准率取了几何平均。这充分验证了HD-SMOTE算法合成样本的机制是合理有效的,这也说明在靠近集群中心的位置合成样本可以有效避免噪声的产生,并且有效提升了分类器对少数类的F-value值。在Class数据集上HD-SMOTE取得的F-value值比ADASYAN低,这是因为ADASYAN算法在类重叠区域大量合成少数类样本,增加了分类器对少数样本分类的查全率和查准率,导致F-value值也随之增加。在其它5个数据集上ADASYAN的F-value值仅次于HD-SMOTE算法,这也很好地验证了ADASYAN可以获得高F-value值的原因。 表3 不同算法下的F-value值 表4给出了5个算法分别在6个不同数据集上的G-mean值。从表可以看出,本文提出的HD-SMOTE算法在这6个数据集上获得G-mean值均优于其它算法,这表明该算法可以有效提升分类器对少数类和多数类的分类精度。前面的分析中发现ADASYAN算法获得的F-value比 HD-SMOTE 高,而在表4中该算法获得的G-mean值却比HD-SMOTE算法低。这是因为ADASYAN算法加强了重叠区域少数类的学习,虽然提高了F-value值但这也加大了重叠区域的多数类样本误分为少数类的几率,从而降低了分类器对多数类的分类精度,因此该算法的G-mean值并不比HD-SMOTE高。 表4 不同算法下的G-mean值 表5列出了5个算法在6种数据集AUC值的比较,可以直观发现本文的HD-SMOTE算法在这6个数据集上的AUC均优于其它算法。在这6个数据集上HD-SMOTE相比于其它算法的AUC值平均提升了2.4%、2.2%、2.7%、4.0%、1.0%和3.0%,可见HD-SMOTE算法比其它算法对数据集的整体分类的准确率有较大提升。这也反映了HD-SMOTE算法机制可以有效缓解不平衡数据集存在的小分离、类内和类间不平衡问题。 纵观表4和表5,可以发现K-SMOTE算法在这6个数据集上的G-mean和AUC值仅次于HD-SMOTE算法,但相较于RAND,SMOTE和ADASYAN算法均有较大幅度的提升,这说明K-SMOTE算法可以有效提升分类器的整体分类准确性。K-SMOTE算法利用K-means聚类算法对整个数据集进行不分标签地聚类,选择出满足失衡比率阈值(集群中多数类样本数量与少数类样本数量的比值)的集群,并且根据这些集群中少数类样本的密度这些集群进行过采样。因此该算法可以较好地解决不平衡数据集的类间和类内不平衡问题,这也是该算法取得较高G-mean和F-value值的主要原因。K-SMOTE算法所得到的集群中可能既包含少数类样本也包含多数类样本,有些集群可能因为不满足失衡比率阈值而被过滤掉。由于这些集群中少数类样本和多数类样本数量差距较大,分类器可能会对多数类样本产生偏倚,所以在这些被过滤掉的集群中需要加强分类器对其中少数类样本的学习。由于K-SMOTE算法过滤掉了不满足失衡比阈值的集群,因此无法加强分类器对这类集群中少数类样本的学习,从而降低了分类器对少数类样本的精确度。这也是该算法的G-mean和F-value值比DH-SMOTE算法低的主要原因,并且K-SMOTE算法对K-means聚类参数很敏感因此参数难以调优。HD-SMOTE算法恰好可以克服这些缺点,HD-SMOTE算法只对少数类样本进行聚类,这很好地克服K-SMOTE算法将少数类和多数类样本聚类为同一个集群的缺陷,并且算法对聚类参数并不敏感,不管在什么情况下HD-SMOTE算法都可以有效加强分类器对少数类样本的学习,增加了分类器对少数类样本和多数类样本的分类精度,因此HD-SMOTE相比较于K-SMOTE和其它算法更为合理。 表5 不同算法下的AUC值 本文提出的方法采用高效的HDBSCA聚类算法结合SMOTE过采样来重新平衡倾斜数据集。它只在安全地区进行过采样,以避免产生噪音。该方法与相关方法的不同之处在于它的新颖性和有效合成样本的方法。样本分布以聚类密度为基础,在稀疏的少数类地区比在稠密的少数类地区合成更多的样本,以克服小分离、类内和类间不平衡问题。实验结果表明,本文提出的方法HD-SMOTE几乎在所有数据集上的F-value,G-mean,AUC均优于其它算法。
3 实验评价指标与参数设置
3.1 实验评价指标

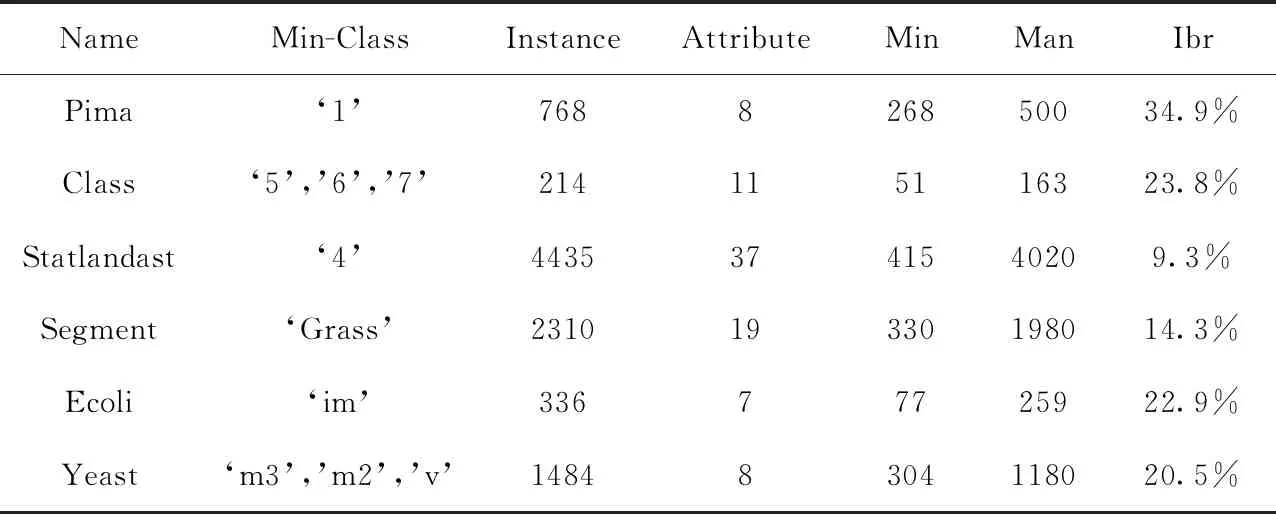
3.2 实验数据
3.3 实验验证与算法参数
4 实验结果及分析
5 结束语

