两个数值积分公式计算效率分析的数值模拟

张光辉

宿州学院数学与统计学院，安徽宿州，234000

数值积分是应用积分理论解决实际问题的重要方法和途径[1]，关于数值积分的经典方法已有很多成熟的公式和理论结论。但是相同的数值积分公式在处理不同问题时的计算效率与实际问题所得模型的复杂程度、被积函数的光滑度等因素有相对复杂的关系，且理论收敛阶和数值收敛阶也有差别，本文主要针对此类问题进行分析和模拟。

1 预备知识

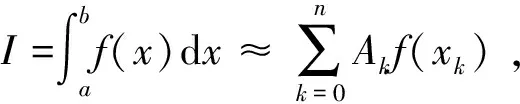
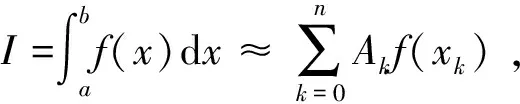
定义3Riemann-Liouville 定义的α阶导数[3]：

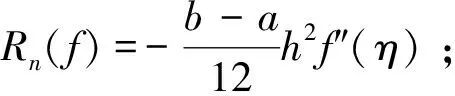
2 主要结果

2.1 模型函数分析

为考查数值方法本身，将数值方法应用于模型函数y=f(x)=xα,α∈(0,4]进行数值模拟，计算复合梯形公式和复核辛普森公式的数值收敛阶，分析公式的数值收敛阶与光滑性之间的关系，即数值收敛阶与α之间的函数关系。

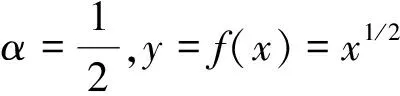
表1 复合梯形公式h与误差Err实验数据

选择Err=Chs函数作为数据(hi,Erri)(i=1,2,…,8)的拟合曲线，两边取对数得:

表2 幂指数α与数值收敛阶s对应实验数据

被积函数f(x)=xα的幂指数α的大小决定其光滑程度，为分析复合梯形公式的数值收敛阶与光滑性之间的关系，用表2数据对α与s的函数关系进行最小二乘拟合，得到

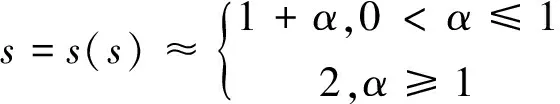
实验结果分析：由定理1知，当被积函数有至少二阶光滑性时，复合梯形公式的理论收敛阶为2，对模型函数的数值模拟结果显示2≤α≤4时，数值收敛阶与理论收敛几乎无差别，数值结果与理论结果相符。1≤α≤2时数据结果表明，虽然y=xα(1≤α<2)不具有二阶连续导数，但数值积分结果显示收敛阶仍近似为2。由实验数据结合梯形公式的渐进展开式[4]可得下面结果。

结果2复合梯形公式的理论收敛阶要求被积函数二阶连续可导，此条件较强，实际只需被积函数一阶连续可导，公式即可达到二阶精度。

类似于复合梯形公式的计算过程，用MATLAB软件编程，用复合辛普森公式对y=f(x)=xα,α∈(0,4]积分，求得α与s的对应实验数据如表3所示。

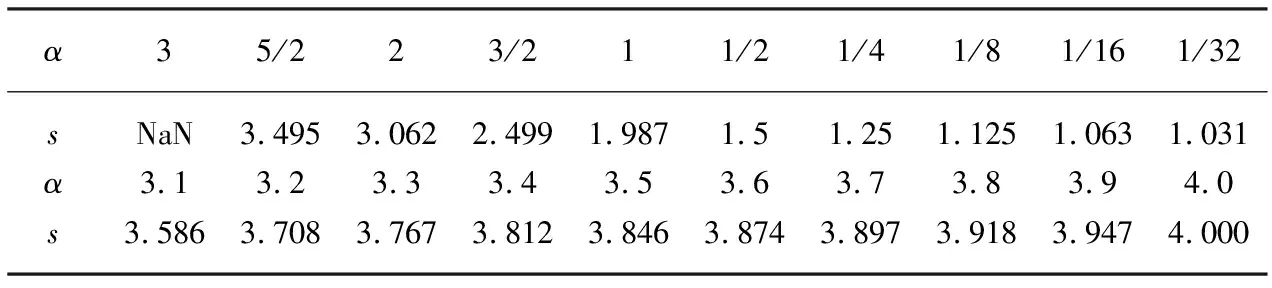
表3 幂指数α与数值收敛阶s对应实验数据

用表3数据对α与s的函数关系进行最小二乘拟合，得到分段函数关系:

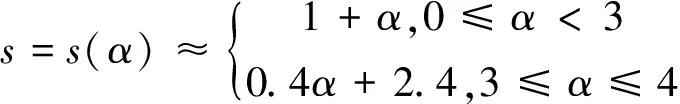
实验结果分析：由定理1知，当被积函数有至少四阶光滑性时，复合辛普森公式的理论收敛阶为4，对模型函数的数值模拟结果显示α=4时，数值收敛阶与理论收敛几乎无差别，数值结果与理论结果相一致。0<α<3时的数据结果表明，y=xα光滑度未达到理论要求，实际计算积分结果达不到应有的精度，数值收敛阶近似为1+α。表明被积函数的光滑度对收敛阶呈近似线性关系。

2.2 算例函数分析

表4 复合梯形公式h与误差Err实验数据

由最小二乘法拟合，得到h与Err满足Err=1.167h1.498，即数值收敛阶为1.498。类似地，可验证复合辛普森公式的h与Err满足Err=0.157 8h1.504，数值收敛阶为1.504，均低于理论收敛阶。

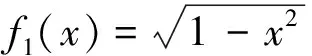
结果3若f(x)为α阶可导函数，若0<α<1,则复合梯形公式和复核辛普森公式的数值收敛阶均为1+α。

即实际计算α(0<α<1)阶可导函数的积分时，复合梯形和复合辛普森公式均达不到应用的精度，故被积函数的光滑度对积分精确度的影响不容忽视。

实验结果分析：被积函数在积分区间上足够光滑无奇性，计算精度不受影响，实际计算时积分公式达到了应用的精度。

表5 复合梯形公式h与误差Err实验数据

表6 复合辛普森公式h与误差Err实验数据

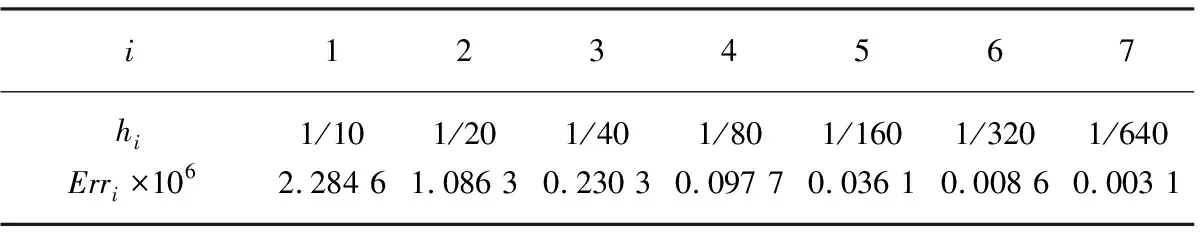
表7 复合梯形公式h与误差Err实验数据

表8 复合辛普森公式h与误差Err实验数据

实验结果分析：数值积分为奇异积分时，复合梯形公式和复合辛普森公式数值收敛阶均达不到理论值，理论精度高的辛普森公式的实际计算效果比复合梯形公式知识稍好一些，与理论结果相差很多，可见奇异积分对数值积分的理论效果影响严重。

3 结 语

通过对复合梯形公式和复合辛普森公式计算效率的数值模拟发现，当被积函数达到理论收敛阶所要求的相应光滑性时，两公式实际计算时积分都能达到应有的精度。但当被积函数存在奇性或光滑度不够时，两个公式的收敛效果均会受到影响，且收敛阶和公式的代数精度、被积函数的光滑程度关系紧密，在一定范围内存在函数关系。因此在数值分析的学习中，加强上机实习，通过上机实验发现新的问题，并用理论进行解释，对深刻理解数值积分公式收敛问题用重要的意义。