例析求向量c=xa+yb中系数x、y的范围

(指导老师：段佳旺)

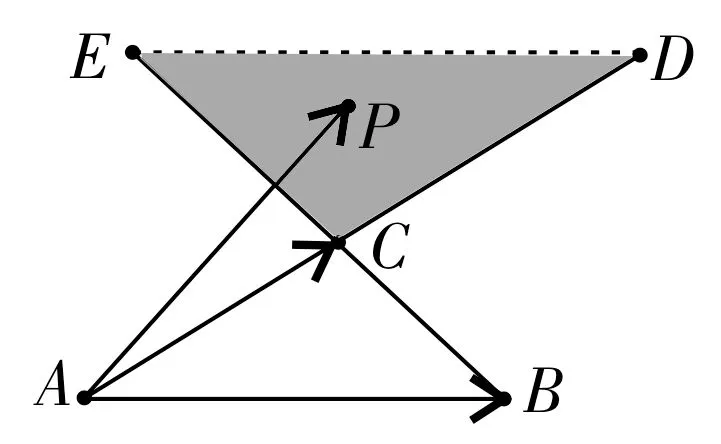
图1

引例如图1,在△ABC中,点P是 边AC,BC的延长线CD,CE所夹的区域内(包括边界)的动点,已知试求2x+3y的取值范围。

一、对向量定理c=xa+yb 的基本认识

图2

例如：如图2,平面内两条相交直线OA,OB将该平面分割成1、2、3、4四个部分,设且点P落在第3部分,则实数m,n的符号应该是___。

图3

分析：如图3,过点P引OA,OB所在直线的平行线PB1,PA1分别交OB,OA所在直线于B1,A1两点,则由得m＞0,由得n＜0。

二、引例的一个错误解法

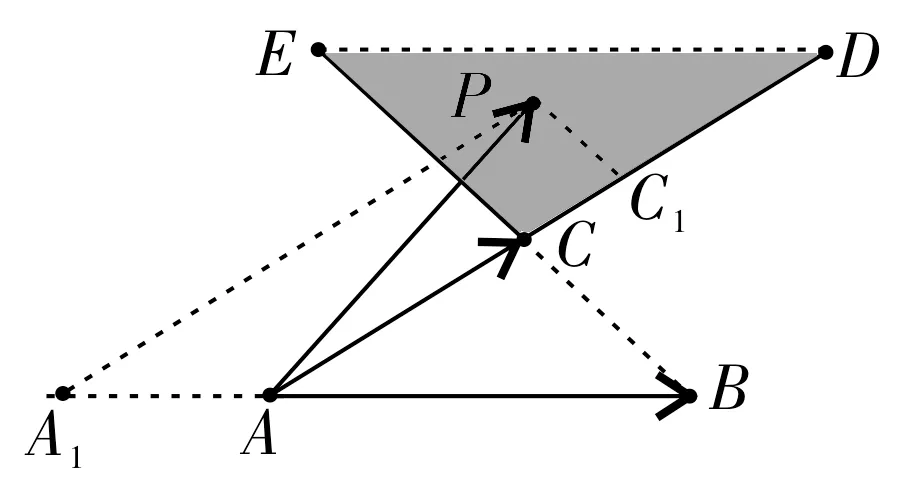
图4

基于对向量定理的基本认识,部分同学会按图4作图。由于点P在可行域内的任意 性,得中的数x、y的范围应该是x≤0且y≥1,从而推导出2x+3y的取值范围是R。

这个解法好像正确,其实只是注意了x、y的来源与几何意义,而忽略了x、y的内在关系,也就是x≤0 且y≥1 的范围是没有错,只是大了一点,不是一个精准的范围。

逆向思维：基向量为,且总是满足x≤0,y≥1,试判断点P所在的范围。

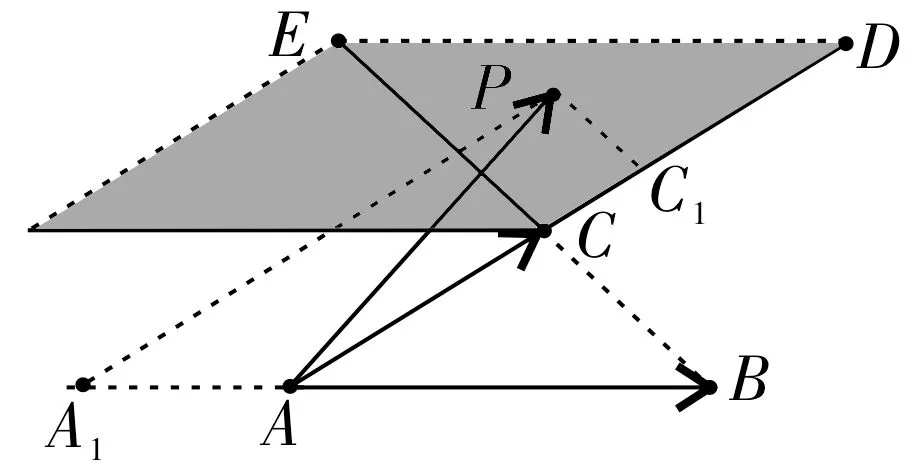
图5

图5 中的阴影部分就是上面问题点P的区域(包括边界),显然覆盖了图4 中的阴影区域。说明不结合x、y之间的联系得到的结论是不精准的。

三、引例正确的解法

四、引例的一个极致解法

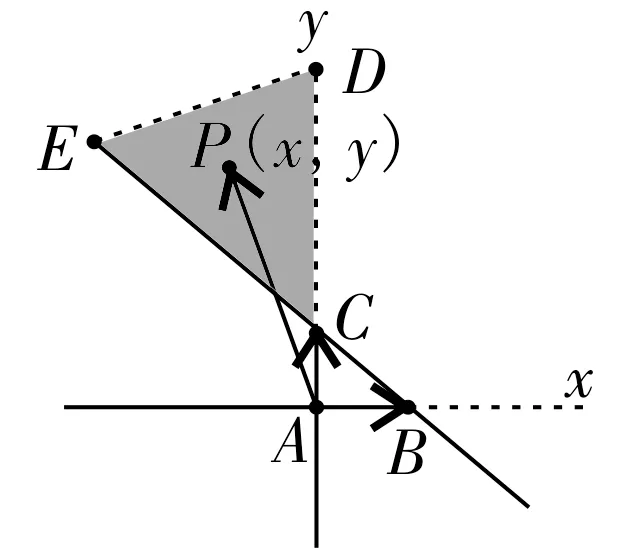
图6

如图6,在直角坐标平面上的△ABC中是正交的单位向量,则问题的中有序数对(x,y)就是终点P的坐标了。由图可以很轻松地得出点P(x,y)满足的约束条件是x≤0 且x+y≥1,目标函数z=2x+3y,z的取值范围是[3,+∞)。