一类具有反循环和anti-abelian结构的4-维李群*

钟世萍，曾姚姚

(赣南师范大学 数学与计算机科学学院，江西 赣州 341000)

1 介绍

附加affinor结构q和度量g的微分流形(M,g,q)的研究受到广泛的关注，其中很多学者研究的是q满足一些二阶的恒等式q2=±id(称为近复结构或仿近复结构)[1-4]，另外K.Yano 和S.Ishihara[5]系统地研究了q满足三阶方程q3+q=0的流形(M,g,q).此外，I. Dokuzova 等人不仅研究了循环结构q满足三阶恒等式q3=±id,q≠id的流形(M,g,q)，而且还探讨了(反)循环结构q满足四阶恒等式q4=id,q2≠id和q4=-id的流形(M,g,q)等等[6-11].最近，I. Dokuzova等人[8,10]讨论了具有特殊循环结构的4-维李群.本文将研究具有反循环和anti-abelian结构的4-维李群.

2 记号和预备知识

设M是一个4-维黎曼流形，在M上任一点p的切空间TpM上赋予一个张量结构S.在给定一个基底时，S是一个反循环矩阵(称S为反循环结构)，具体如下：

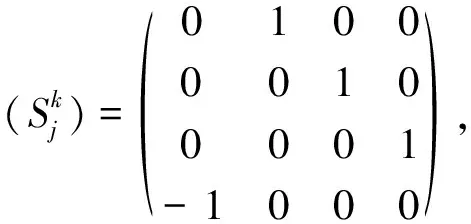
(1)

则S有以下性质S4=-id,

(2)

设度量g和结构S满足

g(Sx,Sy)=g(x,y),x,y∈Γ(TpM).

(3)

由(1)和(3)可得，度量g结构如下：

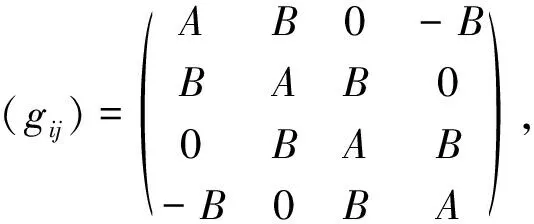
(4)

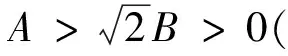
在本文中x,y,z,u都是代表M上的光滑向量场或TpM中向量.本文使用Einstein求和符号，i,j,k,a,b取值始终为{1,2,3,4}.

R(x,y)z=xyz-yxz-[x,y]z,

(5)

R(x,y,z,u)=g(R(x,y)z,u).

(6)

Ricci张量ρ，数量曲率τ以及它的关联的数量曲率τ*分别定义为

ρ(y,z)=gijR(ei,y,z,ej),

(7)

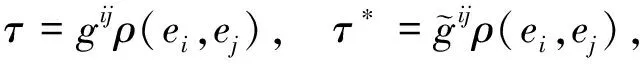
(8)

(9)

3 4-维李群(G,g,S,[,])

设G是4-维实李群，(η,[,])是在基{x1,x2,x3,x4}下的李代数，定义反循环结构S，度量g和括号[,]：

Sx1=x2,Sx2=x3,Sx3=x4,Sx4=-x1,

(10)

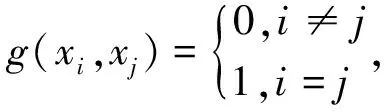
(11)

⎣Sxi,Sxj」=-⎣xi,xj」,i.e.,S是anti-abelian 结构.

(12)

以此方式引入的流形用(G,g,S,[,])表示，称(G,g,S,[,])为具有反循环和anti-abelian结构的4-维李群.

下面，我们考虑一类4-维李群(G,g,S,[,])的曲率性质.设

[x1,x2]=-[x1,x4]=-[x2,x3]=[x3,x4]=λ1x1+λ2x2+λ3x3+λ4x4

[x1,x3]=-[x2,x4]=(-λ2-λ4)x1+(λ1-λ3)x2+(λ2-λ4)x3+(λ1+λ3)x4,

(13)

其中λi∈R.我们发现由(13)确定的李代数(η,[,])所决定的李群(G,g,S,[,])具有一个anti-abelian结构S.上述(13)可以通过(10)(11)以及Jacobi恒等式得到.

引理1xixj可得到如下结果：

x1x1=λ1(x4-x2)+x3(λ2+λ4),x1x2=λ1x1+λ3x3,x1x3=λ3(x4-x2)-x1(λ2+λ4),

(14)

证明由(11)(13)以及著名的Koszul公式2g(xixj,xk)=g([xi,xj],xk+g([xk,xi],xj)+g([xk,xj],xi),我们可以计算xixj如式(14).

引理2曲率张量R=Rijkl的非零部分，结果如下：

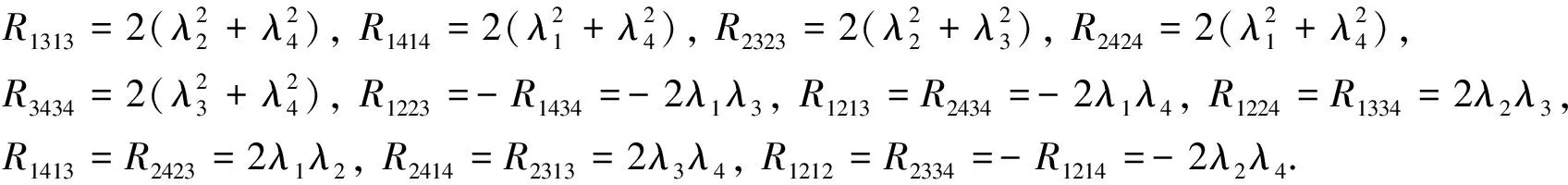
(15)

证明利用(5)(6)(11)(13)(14)，计算得到曲率张量R=Rijkl的非零部分如式(15).

引理3Ricci张量ρ=(ρij)如下：

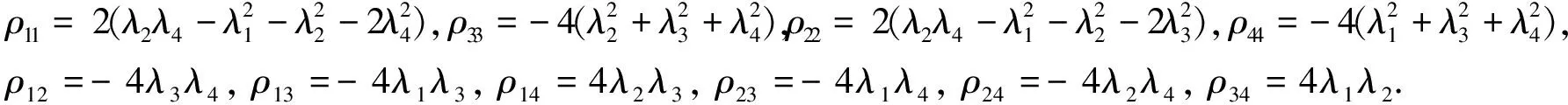
(16)

证明根据(7)(11)(15)，计算得到Ricci张量ρ=(ρij)如式(16).

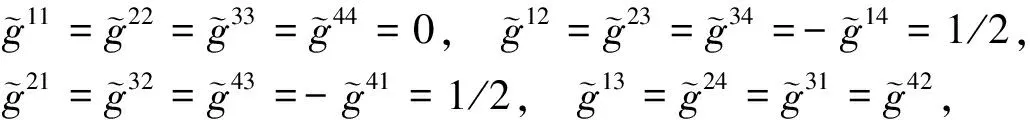
(17)

引理4数量曲率τ以及它的关联量τ*如下：

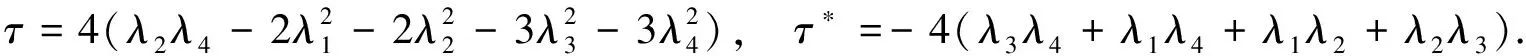
(18)

证明应用(8)(11)(16)(17)，得到数量曲率τ以及它的关联量τ*如式(18).

根据引理2-4，我们有

定理1若(G,η,S)是一个具有如(13)所示的李代数(η,[,])的流形，则：

根据定理1，我们有

推论1若(G,η,S)是一个有如下所示的李代数(η,[,])的流形[x1,x2]=-[x1,x4]=-[x2,x3]=[x3,x4]=λ1x1+λ1x3+λ4x4,[x1,x3]=-[x2,x4]=-λ4x1-λ4x3+2λ1x4,则

推论2若(G,η,S)是一个带有如下所示的李代数(η,[,])的流形

[x1,x2]=-[x1,x4]=-[x2,x3]=[x3,x4]=(λ2+λ4)x1+λ2x2+(λ4-λ2)x3+λ4x4,

[x1,x3]=-[x2,x4]=(-λ2-λ4)x1+2λ2x2+(λ2-λ4)x3+2λ4x4,则

R1213=R2434=-2(λ2+λ4)λ4,R1224=R1334=2λ2(λ4-λ2),

R1413=R2423=2(λ2+λ4)λ2,R2414=R2313=2(λ4-λ2)λ4,R1212=R2334=-R1214=-2λ2λ4.

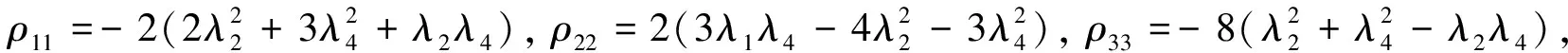
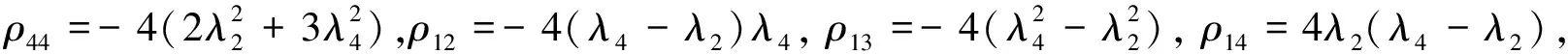
ρ23=-4(λ4+λ2)λ4,ρ24=-4λ2λ4,ρ34=-4(λ4+λ2)λ2.