12-6台体型并联机构位置正解的唯一性分析

尤晶晶，朱俊豪，符周舟，双家炜

（1.南京林业大学机械电子工程学院，江苏 南京 210037；2.江苏省精密与微细制造技术重点实验室，江苏 南京 210016；3.南京林业大学汽车与交通工程学院，江苏 南京 210037）

1 引言

并联机构具有高刚度、高精度等优点，愈发受到关注[1]，其中的六自由度并联机构在传感器[2-3]、模拟器[4]等领域有着非常良好的应用前景。并联机构的运动学正解算法是研究其动力学控制、奇异位形、工作空间等问题的基础，甚至可以说，正解问题不解决，后续工作将举步维艰。针对该问题，国内外学者提出了很多不同的方法，如对偶四元数[5-6]、粒子群[7]、拓扑结构[8-9]。从算法形式来划分，并联机构的运动学正解又可以分为解析法、数值法和半解析法（本质上也是数值法）。其中，数值法适用于任何构型，但运算效率低、过度依赖于给定的初值且容易失根。相比较，解析法有明确的数学表达式，精确度高、运算效率高，有着数值法和半解析法无法比拟的优势，故六自由度并联机构要想得到大规模的实际运用，给出其正解的解析表达式极其重要。

从检索到的文献资料来看，并不是所有的六自由度并联机构都具有解析正解，而且，即使存在解析解，其推导过程也异常复杂，不利于程式化。在文献[10]中提出了一种可完全解耦的六自由度十二杆的台体型冗余并联机构，并给出了其运动学正解的求解流程。然而，进一步研究发现，由于不能确定正解的具体个数，该算法在处理几类特殊位形时存在增根或失根的可能性，这将影响机构的连续性控制。

针对上述问题，通过剖析文献[10]的正解算法，并结合机构拓扑构型内固有的尺度约束关系，对所有可能出现的特殊位形逐类进行分析，确定了新型并联机构的正解数，给出了最终的解析解表达式。最后，通过虚拟试验验证了算法的正确性。

2 结构模型及正解算法

2.1 结构模型

所讨论的并联机构共有12根初始长度为L的可伸缩支链，支链的一端通过一般球铰链与静平台相连，另一端通过复合球铰链与动平台相连，且每两条支链共用1个复合球铰链；动平台是边长为2n的正方体，静平台是边长为2（n+L）的空壳状正方体；初始状态下，动平台与静平台的中心点重合，且姿态相同；六个复合球铰链分别位于动平台的左上棱、后上棱、右后棱、右下棱、左前棱、前下棱的中点位置，如图1所示。

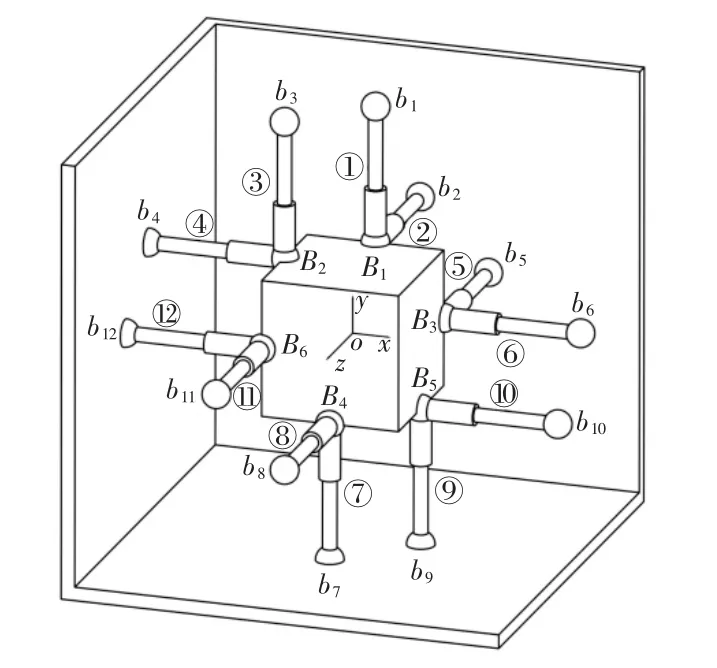
图1 初始位形下的机构简图Fig.1 Schematic Diagram of Mechanism in the Initial State

2.2 正解算法

以静平台的中心为原点，固连三维直角坐标系｛o-x-y-z｝，其中，x、y、z轴分别指向静平台右侧面、上侧面、前侧面的中心点。将静平台上十二个一般球铰链的中心点记为b1～b12，动平台上六个复合球铰链的中心点记为B1～B6，动平台的中心点记为P，十二条支链记为①～12○，其实时杆长表示为li。分别将B1、B2、B3、P点的笛卡尔坐标表示为（x1，y1，z1）、（x2，y2，z2）、（x3，y3，z3）、（x0，y0，z0），因此，正解算法中共有十二个未知量。任意给定一组杆长，容易推导出y1、z1、x2、y2、x3、z3、x0、y0、z0这9个量的解析表达式[10]。然而，在特殊位形时，x1、y3、z2可能会出现多解。为便于讨论，这里首先对多解的情况进行分组，如表1所示。

表1 多解情况的分组Tab.1 The Division of Situations of Multiple Solutions

3 正解唯一性分析

3.1 两组解的情况分析

以位形1为例，2、3的分析过程与此类似。根据动平台上复合球铰链之间、复合球铰链与动平台质心之间的固有尺度约束关系，建立未知量之间的约束方程：

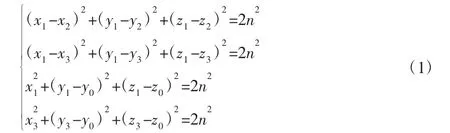
当x2≠0且x3≠0或者x2=0且x3≠0或者x2≠0且x3=0时，x1均具有唯一解。

构型中，B1B2平行于B3P，且B1、B2、B3、P四点共面。因此，当x2=0且x3=0时，x1只有零解。

综上所述，当x0，y0，z0中只有一个为0时，新型并联机构的运动学正解是唯一的。

3.2 四组解的情况分析

以位形4为例，位形5、6的分析过程与此类似。约束方程为：

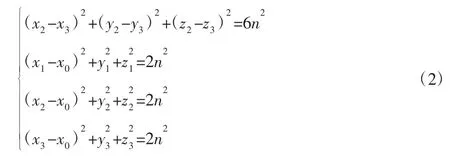
当z1≠0且y1≠0或者z1=0、y1≠0且z3≠0时，y3、z2有唯一解。

当z1=0、y1≠0且z3=0时，y3有唯一解；另外，根据“四点共面”，z2的值等于0。同理，当z1≠0且y1=0时，y3、z2有唯一解。

当z1=y1=0时，若y2=z3=0，则由“四点共面”可得z2=y3=0；若y2=0且z3≠0，则z2有唯一解，且由“四点共面”得到y3=0；若z3=0且y2≠0，同理可得，y3、z2只有唯一解；若z3≠0且y2≠0，由“四点共面”可得z2≠0、y3≠0，且：

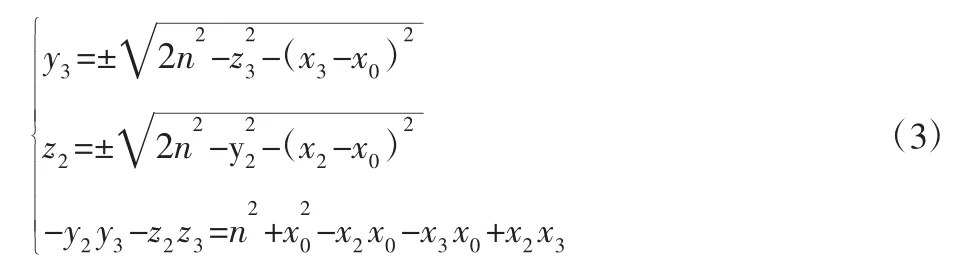
为更好地描述式（3）中变量之间的几何关系，以y3、z2为正交轴建立辅助笛卡尔坐标系，如图2所示。

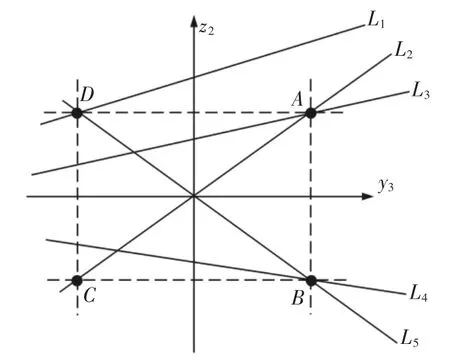
图2 辅助笛卡尔坐标系Fig.2 The Auxiliary Cartesian Coordinate System

式（3）中的前两个方程在坐标系中表示为四条直线，如图2中的虚线所示，它们的四个交点A、B、C、D关于原点对称。第三个方程为一条斜线，理论上它与A、B、C、D可能有一个交点（如L1、L3、L4等），也可能有两个交点（如L2、L5等），而后者一定对应着斜线过原点的情况。由于z1=y1=y0=z0=0，故B1、P点在x轴上；又因为B2与B1、P的距离相等，故B2在x轴上的投影为B1、P的中点。同理，B3在x轴上的投影也为B1、P的中点。又由于n＞0，故第三个方程对应的斜线一定不可能过原点。综上所述，当x0，y0，z0中有两个为0时，正解是唯一的。

3.3 八组解的情况分析

约束方程为：

3.3.1 位形7

以x2=0为例分析，其它五种情况与此类似。

结合式（4）可知，x1、y3有唯一解。

3.3.2 位形8

仅分析三种典型情况，其它与此类似。

当x2=x3=0时，由“四点共面”关系得到x1、y3、z2的唯一解。

当z1=y1=0时，x1、z2、y3有唯一解。

当x2=z1=0时，x1、z2、y3有唯一解。

3.3.3 位形9

仅分析两种典型情况，其它与此类似。

当x2=x3=z1=0时，由“四点共面”关系得到x1、y3、z2的唯一解。

当x2=z1=y2=0时，z2有唯一解。此时，B2、P点都在z轴上；又因为B2P平行于B1B3，所以B1B3也平行于z轴，即y3=y1且x1=x3。因此，x1、y3的解唯一。

3.3.4 位形10

以x2=x3=z1=y1=0为例进行分析。由“四点共面”得到x1=0；再结合式（4），z2、y3的解唯一。

3.3.5 位形11

以x2=x3=z1=y1=y2=0为例进行分析。z2的解唯一；再结合“四点共面”关系，得到x1=y3=0。

3.3.6 位形12

直接由“四点共面”关系得到：x1=y3=z2=0。

3.3.7 位形13

当上述行列式的值等于零时，方程组发生退化；但此时由“四点共面”的几何特征关系可得：

综上，当x0，y0，z0全部为0时，正解也是唯一的。

4 虚拟试验的算例验证

运用Mathematica软件建立新型并联机构的虚拟样机，如图3所示。其中，质量块的边长和支链的初始长度分别设置为30mm、25mm。虚拟试验中，通过给定并联机构12条支链的长度，可以测量出动平台的位置、姿态数据以及所有特征点的坐标值；相反地，通过给定动平台的位置、姿态或者三个非共线特征点的坐标值，也可以测量出12条支链的长度数据。

图3 并联机构的虚拟样机Fig.3 The Virtual Prototype of Parallel Mechanism

给出三个典型算例，首先，基于正解算法计算特征点的坐标值；然后，将理论计算值与试验测量数据进行对比，如表2所示。结果显示，该新型并联机构具有确定的、唯一的运动学正解，且计算值与试验值完全吻合，表明这里的算法是正确、有效的。

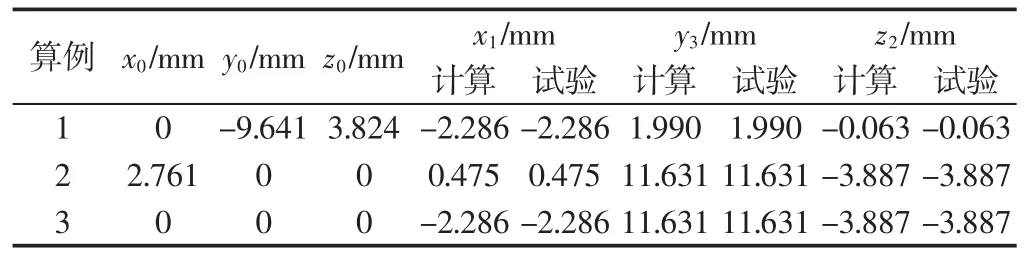
表2 并联机构正解模型的算例验证Tab.2 Exam ples of Forward Kinematics of Parallel Mechanism

5 结论

针对一种新提出的12-6台体型并联机构，对其正向运动学算法进行了剖析，从理论上证明了该机构的运动学正解不存在增根和失根的现象，并推导出了全解析表达式。进一步通过虚拟试验验证了所提出方法的正确性和有效性。研究结果表明，当给定一组合适的杆长时，并联机构动平台的位姿能够唯一确定，这为机构后续的实时、有效控制奠定了理论保障。下一步工作计划是从输入、输出量的解析映射出发，推导并求解杆长协调方程。