3-UPU并联自动调平机构控制系统设计

朱志强，熊艳红

（湖北职业技术学院，湖北 孝感 432000）

1 引言

随着《中国制造2025》发展战略的提出，国内企业不断升级改良生产制造设备，越来越关注产能、自动化率、成本等问题之间的矛盾。提高自动调平机构的定位精度已成为企业提高产品质量、扩大效益的重要手段[1-2]。目前，我国自动调平机构的构型与国外相比，还存在加工精度较低、形位公差偏大、轨迹跟踪误差较大等缺陷。大部分的自动调平机构为串联开环的构型设计，这种连接形式的调平机构往往存在定位精度低、末端件惯性大、运动惯量大、误差累积等缺点[3]。因此，如何降低自动调平机构的调平误差，越来越受到学者们的重视。文献[4]研究了一种适用于斜坡场合的自动调平机构，通过解析法得到了各推杆间的关系和极限运动角度，但是通过运动学建模来控制机构调平精度的方法不能很好地反映机构各推杆与外界输入间的关系。文献[5]设计了一种果园升降平台的自动调平机构，并基于模糊PID控制策略来调整机构的姿态，但是缺少对模糊PID控制器稳定性分析的论证。文献[6]设计了一种多自由度的并联调平机构，并研究了高次静不定问题对机构调平精度的影响，但是多自由度的并联机构的构型设计和动力学求解十分困难。文献[7]通过SimMechanics设计了一种六点支撑式的自动调平机构，并通过Simulink仿真了机构的调平特性，但是SimMechanics模型与实体模型的重合度不高。为了提高调平机构的调平精度，设计了一种少自由度的3-UPU并联调平机构，并设计了一种PI鲁棒滑模控制器来提高机构的调平精度，通过机构各方向的调平误差分析，验证了调平机构的有效性。

2 调平机构构型设计

2.1 3-UPU并联机构构型分析

3-UPU并联机构主要由动平台、定平台和三条对称的支链构成，其单一支链包括两个虎克铰U副和一个移动P副，两个虎克铰U副分别与机构的动平台、定平台相连接，虎克铰U副间通过移动P副串接，移动P副为驱动副，为机构的运动提供动力。机构的动定平台为等边三角形，在机构定平台和动平台的中心点分别建立机构的静坐标系O-XYZ和动坐标系o-xyz，3-UPU并联机构示意图，如图1所示。

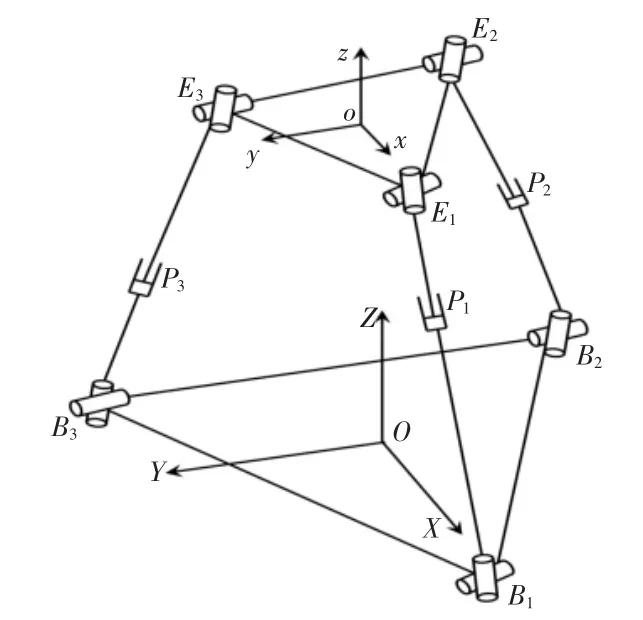
图1 3-UPU并联机构简图Fig.1 Diagram of 3-UPU Parallel Mechanism

2.2 机构特性分析

由于3-UPU并联机构具有对称性，只需取其单一支链UPU进行分析即可。基于螺旋理论，对3-UPU并联机构进行运动特性分析，在虎克副外侧轴心建立直角坐标系O-XYZ，假设支链与X轴的夹角为α，3-UPU并联机构支链螺旋示意图，如图2所示。

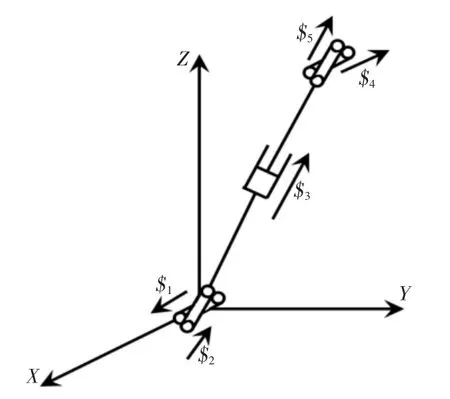
图2 UPU支链螺旋示意图Fig.2 Screw Schematic Diagram of UPU Chain

根据螺旋理论，可得到支链的运动螺旋为：

由反螺旋理论可知，机构的反螺旋是对运动螺旋的结构约束，表示机构在三维空间受到的运动约束与支链螺旋系的反螺旋是等价的[8]。式（1）组成了UPU支链的螺旋系，由反螺旋理论分析可得机构末端（动平台）仅有一个约束。由Matlab软件计算可得机构的反螺旋为：

由上式反螺旋可知，机构的支链仅受一个约束绕z轴转动的力偶的约束。由线矢和旋量在不同几何空间下的线性无关性可确定，机构的反螺旋分别对动平台施加了x，y，z方向的力偶约束，即3-UPU并联机构的运动特性为沿x，y，z方向的平移。

3 3-UPU并联机构动力学建模

机构动力学分析的主要目的是研究机构在外界作用力下产生的运动，以及力与运动间的相互关系。机构的动力学分析不仅是机构运动轨迹规划设计的重要组成部分，而且是机构调平精度控制研究的基础。由于Lagrange方程无需求解机构的角速度和加速度，且推导过程较简单。因此，采用Lagrange法来建立3-UPU并联调平机构的动力学模型。为了便于建立机构的动力学方程，假设机构各杆件的质量均匀分布，且各铰链间的运动副质量和摩擦力忽略不计。

由于在实际的运动过程中，机构连杆运动的角速度较小，可以忽略其转动动能，只需计算其移动动能。另外，驱动件仅存在直线运动，所以驱动件不存在转动动能。因此，机构动能主要由动平台的动能、连杆的移动动能和驱动件的移动动能三部分构成。

（1）动平台的动能

式中：q，q˙—机构的广义位移和速度；Md—机构动平台的惯性矩阵，下同。

（2）连杆的移动动能

式中：i=1，2，3，mli，vli—第i个连杆的质量和质心角速度；Mi—机构连杆的惯性矩阵。

（3）驱动件的移动动能

式中：i=1，2，3，mfi，vfi—第i个驱动件的质量和移动速度；Mf—驱动件的惯性矩阵。

（4）机构的势能

式中：i=1，2，3，md—动平台的质量；zd，zli，zfi—动平台质心、第i个连杆质心和第i个驱动件质心的坐标值。

由Lagrange方程：

可得到机构动力学方程的简化形式为[9]：

式中：M—3×3阶惯性矩阵；C—3×3阶离心力矩阵；G—3×3阶重力矩阵；τ—控制输入。

4 PI鲁棒滑模控制

4.1 控制系统设计

相对于传统的串联调平机构，并联调平机构具有多闭环、非线性的特点，其控制系统是一个复杂的MIMO多输入多输出系统。系统的耦合性、时变性等不确定性因素对调平机构的定位精度有很大的影响，必须选择一种合适的控制策略来提高机构的定位精度。传统的控制算法应用在非线性系统时，会产生很大的轨迹跟踪误差，从而影响机构的调平精度。在传统PI控制的基础上，引入鲁棒滑模控制算法，来提高控制精度。鲁棒控制（Robust Control）和滑模控制（SlidingMode Control）可以根据被控对象和外部扰动变化，实时修正自身特性。且能在一定的参数摄动下，维持控制系统的某些性能不发生改变。

基于3-UPU并联调平机构的非线性特征，可采用S-Function函数来描述机构的动力学方程和系统的控制律，不仅可以使建立的控制框图更加接近机构的实际情况，而且可以使系统的轨迹跟踪误差降至最低。3-UPU并联调平机构的控制系统框图，如图3所示。其中，SineWave为机构输入的理想信号源，Derivative1和Derivative为微分器，Clock为计时器，S-Function1为第2节建立的动力学方程，S-Function为系统的控制律，可切换PI控制和PI鲁棒滑模控制两种方式，Transfer Fcn为低通滤波器函数，主要用于降低系统抖振和高频信号。

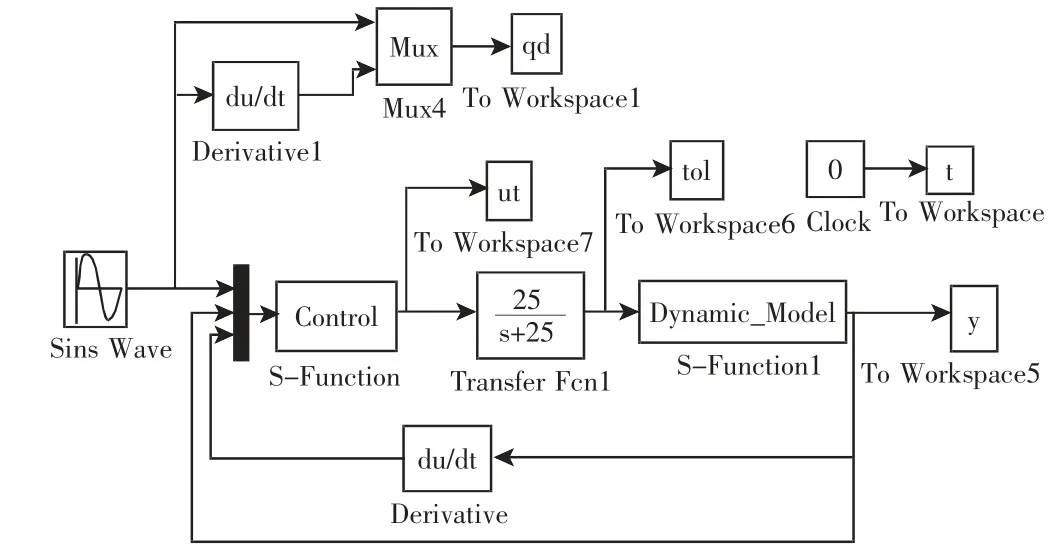
图3 控制系统框图Fig.3 Block Diagram of Control System

4.2 控制器设计

综合式（8）和Lagrange法，在考虑外加干扰τd时，可得到机构的动力学方程为：

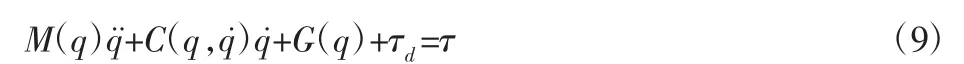
在实际的工程运用中，矩阵M（q），C（q，q˙），G（q）通常不是很精确的，可将其表示成：

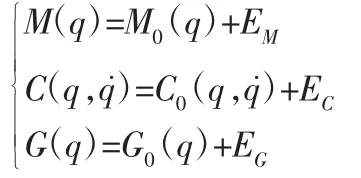
式中：EM，EC，EG—矩阵M（q），M（q，q˙），G（q）的建模误差。

假设系统的跟踪误差为e（t）=qd（t）-q（t），qd（t）为期望的轨迹信号，q（t）为实际的轨迹信号。滑模函数为r=e+Λe，Λ＞0。定义q˙r=r+q˙，则q˙r=q˙d+Λe，q¨r+r˙+q¨=q¨d+Λe˙，由式（9）可得：

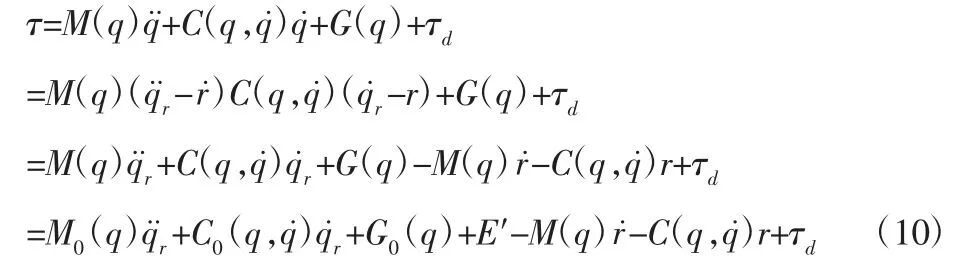
其中，E′=EMq¨r+ECq˙r+EG。

控制器的设计如下：

式中：Kp＞0，Ki＞0，τm—基于机构名义模型的控制律；τr—系统的鲁棒修正项。

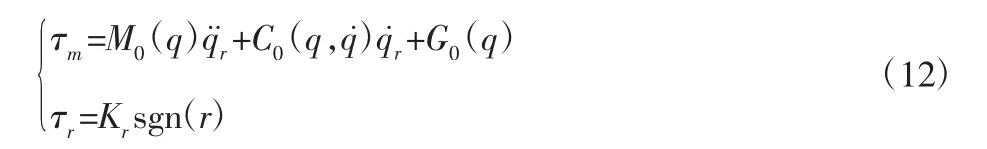
其中，Kr=diag［kri］，kri≥|Ei|，i=1，…，n，E=E′+τd。由式（9）至式（12）有：

4.3 控制器的稳定性分析

假设积分形式的Lyapunov函数为：

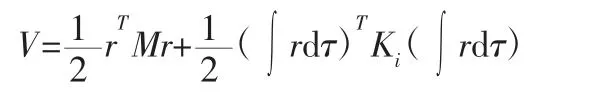
对称性，有rT（M˙-2C）r=0，所以：

将式（13）代入式（14）得：

因为kri≥|Ei|，则V˙≤-rTKpr≤0。

收敛性分析上式可知：

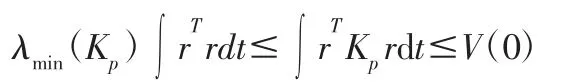
式中：λmin（Kp）—Kp的最小特征值。

由于V（0）和λmin（Kp）为正实数，则e连续且当t→∞时，e→0，e˙∈Ln2。由V˙≤-rTKpr≤0可知0≤V≤V（0），∀t≥0，则V（t）∈L∞，从而说明有界。根据e∈Ln2∩Ln∞，e∈Ln2且q˙d，q¨d∈Ln∞可知q˙r，q¨r∈Ln∞，另外基于式（13）和式（10）且r∈Ln2，qd，τr∈Ln∞可知r˙∈Ln∞，τ∈Ln∞。由于r∈Ln2，r˙∈Ln∞，所以当t→∞时，r→0，从而保证了t→∞时，e˙→0。

由上述的分析可知，PI鲁棒滑模控制满足滑模控制的三大要素，控制器是稳定的[10]。

5 仿真分析

假设机构的理想轨迹信号qd1=qd2=qd3=sin t，M0=0.6M，C0=0.8C，G0=0.8G，采用式（11）的控制律，取Kp=diag｛80 80 80｝，Ki=diag［100 100 100］，kr=diag［20 20 20］，Δ=diag［2 2 2］，仿真时间10s。基于Matlab的Simulink模块和S-Function函数对3-UPU并联调平机构的控制系统进行设计，分别采用PI控制和PI鲁棒滑模控制对调平机构进行仿真分析，得到机构三个方向的调平误差曲线，如图4～图6所示。

由图4和图6可知，调平机构在2s的时间内，PI控制和PI鲁棒滑模控制都出现了一定的波动状况，但是随着鲁棒滑模算法抗扰动和实时修正运算的进行，PI鲁棒滑模控制的调平误差逐渐减小，而PI控制的调平误差仍然较大。这表明PI鲁棒滑模控制的效果更好，可以使3-UPU并联调平机构得到较小的稳态误差和更佳的调平精度。

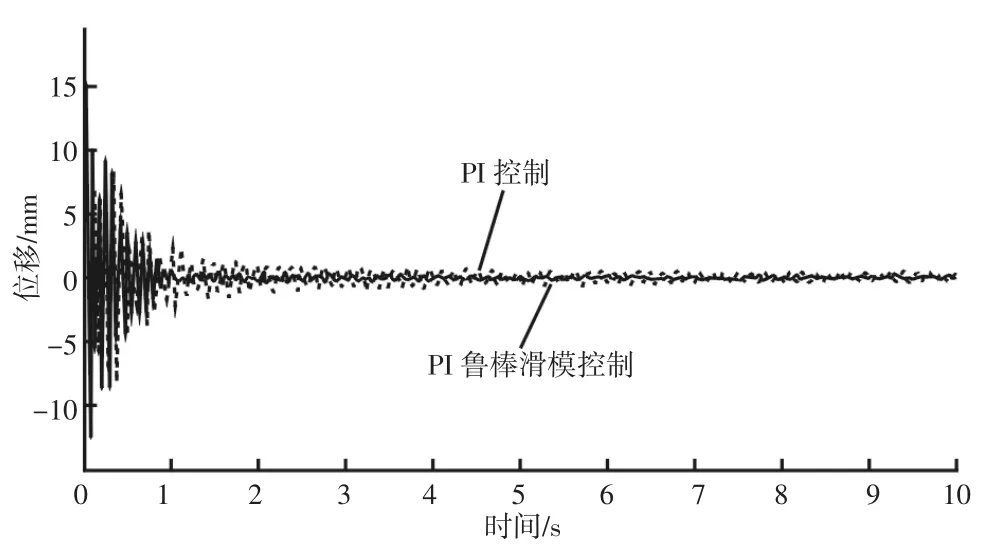
图4 机构沿X轴平移的调平误差曲线Fig.4 Leveling Error Curve of Mechanism’s X Axis

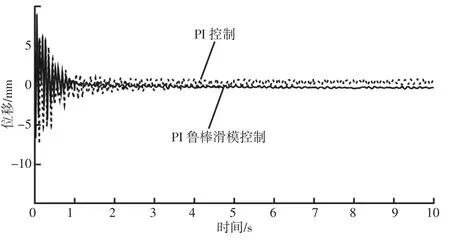
图5 机构沿Y轴平移的调平误差曲线Fig.5 Leveling Error Curve of Mechanism’s Y Axis

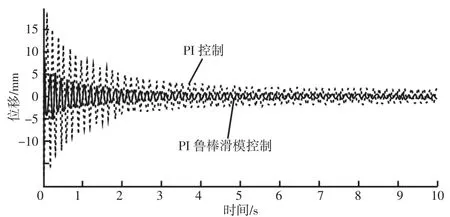
图6 机构沿Z轴平移的调平误差曲线Fig.6 Leveling Error Curve of Mechanism’s Z Axis

6 结论

基于螺旋和反螺旋理论，设计了一种新型调平机构—3-UPU并联调平机构。采用拉格朗日法，得到了3-UPU并联调平机构的动力学方程，为机构的控制仿真提供了控制对象。在PI控制策略的基础上，引入鲁棒滑模控制算法，设计了一种PI鲁棒滑模控制器，并对并联调平机构各方向的调平误差进行了仿真分析。结果表明：该PI鲁棒滑模控制器可以满足调平机构调平精度的要求，且具有稳态误差小和抗干扰性强等优点，为调平机构的研究提供了一种参考方案。