二重滚珠式动力吸振器的参数设计

向重卫，张小龙

（西安建筑科技大学机电工程学院，陕西 西安 710055）

1 引言

振动在工程中随处可见，大部分振动是有害的，有害的振动能加快机械设备的磨损，使其性能和工作精度降低。所以对于振动控制的研究具有特别重要的意义。动力吸振器应用已经历一个多世纪，对其研究已有相对成熟的理论。由于动力吸振器结构简单，便于制造，可靠性高，故而广泛应用于工程中[1]。

在吸振器研究方面，文献[2]给出n级并联和n级串联式动力吸振器优化的通用模型，并且介绍了定点优化和数值优化两种方法。文献[3]利用达朗伯原理建立了附有动力吸振器的两自由度振动系统数学模型，并进行了最优化设计。文献[4]对双滚子型动力吸振器进行了优化设计，得出了最优振幅放大率曲线。文献[5]提出了一种新型滚珠式多向动力吸振器，并且进行了参数优化。文献[6]研制一种双自由度自调谐吸振器，可在竖直平动和横向摆动两个方向上调节自身的固有频率，实现两个方向的吸振。文献[7]利用两球同向旋转时在接触点处逆向运动产生阻尼力，设计了一种两球转动式吸振器。文献[8]分别以等效悬臂梁模型和垂尾模型为例，参照所设计的电涡流耗能动力吸振器的具体参数，通过有限元仿真分析验证了多重动力吸振器在等效悬臂梁模型和垂尾模型中的吸振效果。文献[9]针对既有研究对人体各部位进行单独分析时自由度较少的限制，提出了人体坐姿九自由度垂向振动动力学模型，同时对模型进行振动响应分析。文献[10]构建了双级摆线钢球减速器动力学分析模型，对其弯曲与扭转受迫振动进行了研究。

据此，理论设计了一种由简单球体和球面组成的二重滚珠式吸振器，通过拉格朗日方程建立动力学模型，运用解析及数值计算对其进行了参数优化设计。

2 吸振器理论

2.1 吸振器动力学模型及微分方程

模型，如图1所示。振动主体M用刚度为k的弹簧和阻尼系数为c的阻尼器与基础相联，两个质量和半径为m1、m2和r1、r2的吸振球在半径分别为R1、R2的圆弧面内运动。系统平衡时，吸振球处于圆弧面最底部，两球相隔距离为a，弹簧无伸长，在系统上作用有一F cosωt的激励。建立固定坐标系O-XY，如图1所示。以图示为坐标原点，取振动主体的水平位移z及吸振球心绕球面中心O′1、O′2的角位移θ1、θ2为广义坐标。

图1 吸振器动力学模型Fig.1 Dynamic Model of Vibration Absorber

设两吸振球心在O-XY坐标系中的坐标分别为（x1、y1）（x2，、y2），则有：

假设吸振球沿圆弧面轨道作无滑动的纯滚动，并设吸振球从圆弧面最底部的平衡位置开始滚动到图1位置时滚动角度为φ，如图2所示。则有下述关系（两个吸振球情况相似）：

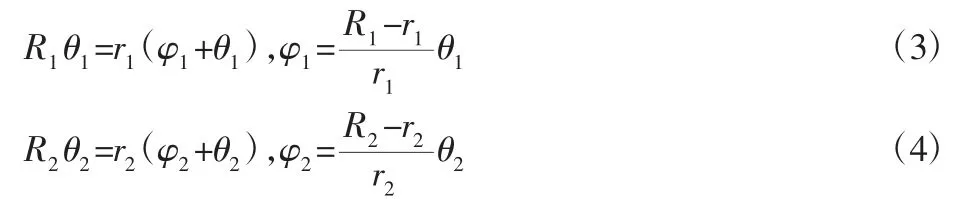
系统的动能T、势能U和耗散函数V分别为：

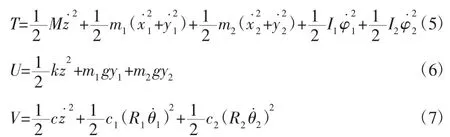
当系统作用有外部激励F cosωt时，结合式（5）～式（7），根据拉格朗日方程，可列出系统的运动微分方程如下：

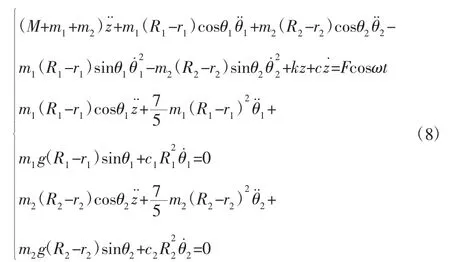
假设吸振球在其平衡位置做微小振动，θ1、θ2为微小量。即θ＝O（ε），取sinθ≈θ，cosθ≈1略去O（ε3）及其以上量级小量，则式（8）对应的无量纲方程式为：

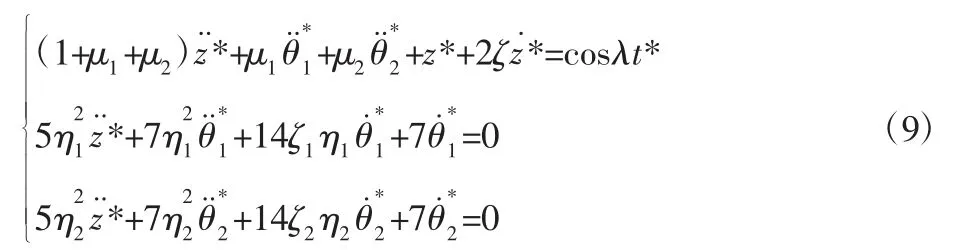
图2 吸振球滚动模型Fig.2 Vibration Absorption Ball Rolling Model

2.2 求解系统的振幅比

式（9）第一个方程右边加上j sinλt*，等号右边变为ejλt*，实部为原方程解，假设解为：z*=Zejλt*，θ*1=Θ1ejλt*，θ*2=Θ2ejλt*

将假设解带入，则（9）可化为：

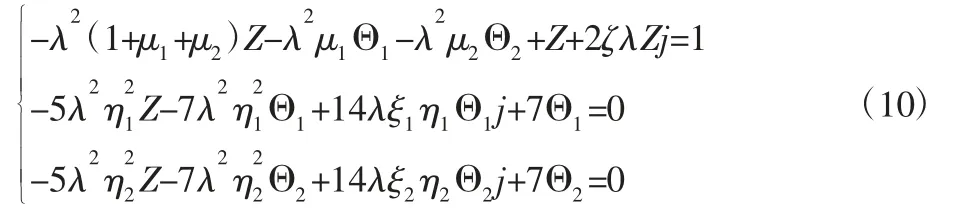
解方程组（10）可得：

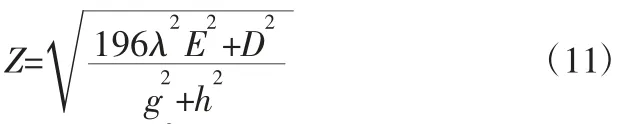
其中，D=A1A2-196ξ1η1ξ2η2λ2，E=ξ1η1A2+ξ2η2A1，g=CD-28ζλ2E-λ2μ1B1A2-λ2μ2B2A1，h=14λEC+2ζλD-14λ3μ1B1ξ2η2-14λ3μ2B2ξ1η1

建立以λ—横坐标，Z—纵坐标的坐标系，则Z随ξ1、ξ2和μ1、μ2的变化规律，如图3、图4所示。

图3 吸振球阻尼比对系统振幅的影响Fig.3 Effect of Damping Ratio of Vibration Absorbing Sphere on System Amplitude

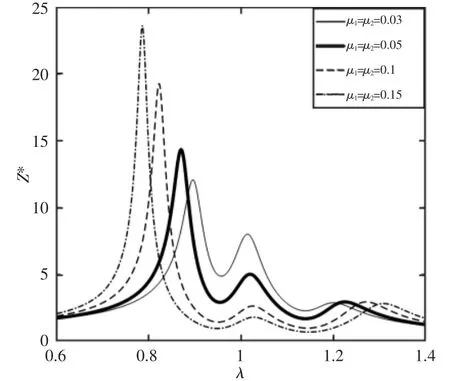
图4 吸振球质量比对系统振幅的影响Fig.4 Effect of Mass Ratio of Vibration Absorption Ball on System Amplitude

从图3可以看出，无论两阻尼比如何变化，系统的振幅比曲线总是过三个定点，我们可以利用此特点来对吸振器进行参数优化设计。从图4可以看出，吸振器的质量比越大，吸振效果越好，但是在系统工作中，由于受到现实条件的限制，吸振器不可能达到理论中的足够大，我们会选择一个合适的质量比来进行研究。

3 动力吸振器的最优参数设计

3.1 三定点定理

从图3中可知，Z随两吸振球的阻尼比ξ1、ξ2的变化总是过三个定点，而这三个点的振幅比在已知条件确定的情况下是无法改变的，在吸振器质量比选定合适的情况下，如果适当调整其参数（吸振球的阻尼比ξ1、ξ2和固有频率比η1、η2），使得这三个定点保证基本平齐，且在定点处均取得极大值（或接近极大值），则在系统工作状态中的振幅比均不会超过三个定点，可以保证系统在工作中共振点附近的振动稳定性，有效降低强迫振动的响应，从而保证系统稳定工作，我们可以利用这个特性来进行优化设计。三定点在图中位置，如图5所示。

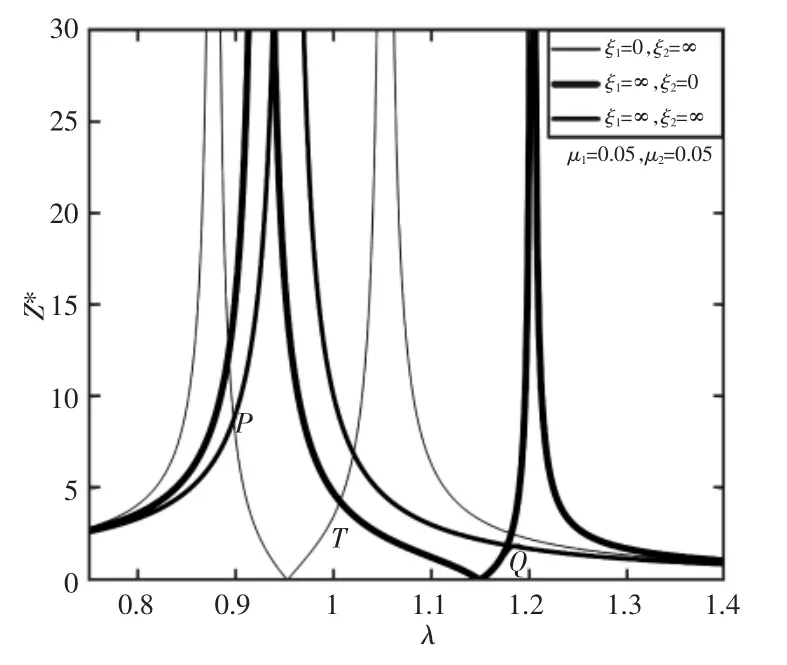
图5 系统振幅三定点Fig.5 Three Fixed Point of System Amplitude

3.1.1 三定点纵坐标的确定

可以发现，图5的三条曲线两两相交，并且每两条曲线就会有两个交点，一共形成6个交点，而我们所说的三个定点式图线相交而成的最内侧的三个点。由于不同曲线的相交会形成不同的交点，并且同一曲线在其渐近线两侧与其他曲线形成的交点也不相同，下面我们将分情况来讨论相交定点的形成。

（1）ξ1=0，ξ2=∞的情况

将C、D、E带入Z中并消去无穷小可得：

其中，“+”代表图线在渐近线左侧，有交点T；“-”代表图线在渐近线右侧，有交点P，如图6所示。

图6 定点P的确定Fig.6 Determination of Fixed Point P

（2）ξ1=∞，ξ2=0的情况

将C、D、E带入Z中并消去无穷小可得：

其中，“+”—图线在渐近线左侧，有交点Q；“-”—图线在渐近线右侧，有交点T，如图7所示。

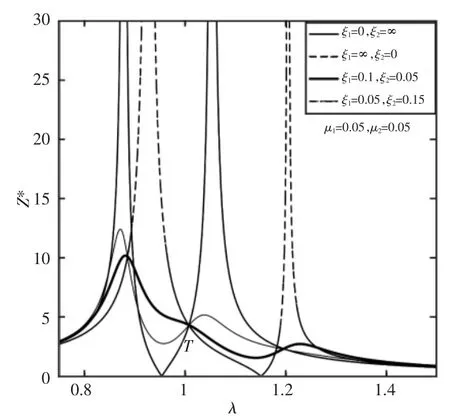
图7 定点T的确定Fig.7 Determination of Fixed Point T

（3）ξ1=∞，ξ2=∞的情况

将C、D、E带入Z中并消去无穷小可得：

其中，“+”—图线在渐近线左侧，有交点P；“-”—图线在渐近线右侧，有交点Q，如图8所示。

3.1.2 三定点横坐标的确定

使定点的纵坐标相同列出等式计算化简可以得出关于λ的表达式，此为定点的横坐标。

即有：

将A1、B1、C代入式（15）并计算可得：

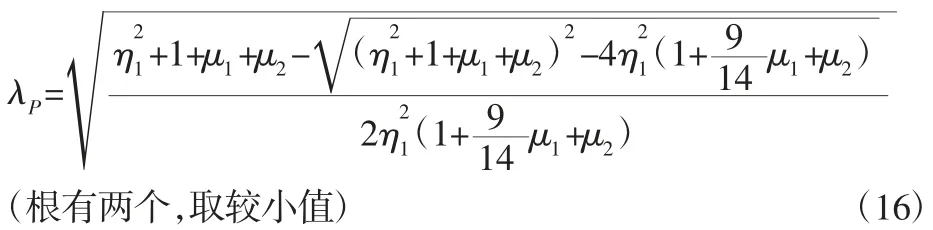
即有：

将A2、B2、C代入式（17）并计算可得：

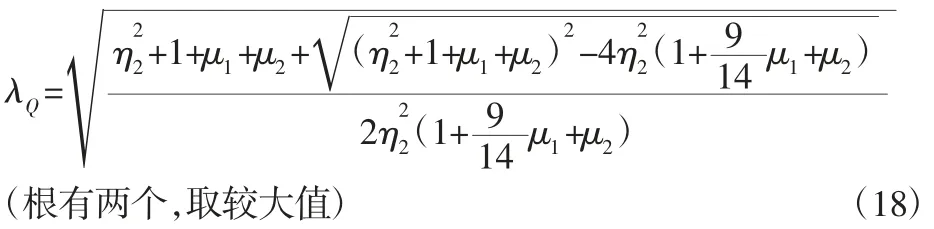
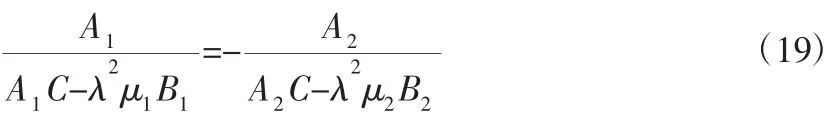
将A1、B1、A2、B2、C代入式（19）可得：

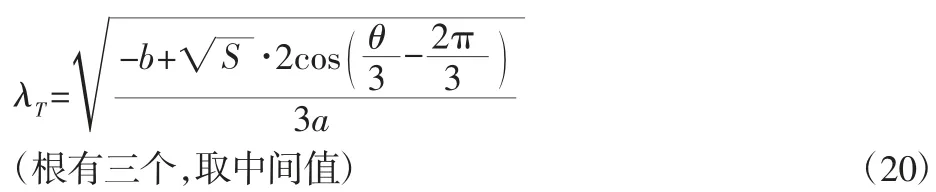
图8 定点Q的确定Fig.8 Determination of Fixed Point Q

3.2 最优频率比及最优阻尼比

（1）P、Q等高条件

将P、Q代入Zξ1=∞，ξ2=∞有：即：

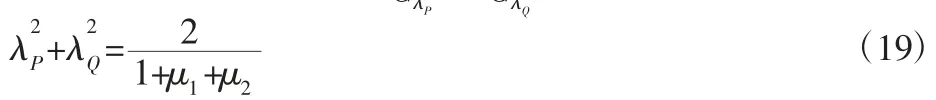
（2）P、T等高条件

将P、T代入

Zξ1=∞，ξ2=∞、Zξ1=0，ξ2=∞有：，即：

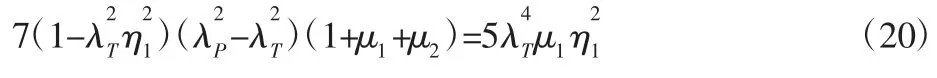
可以看到，式（19）、式（20）是关于μ1，μ2，η1，η2四个参数的方程，然后选择可以测得的合适的参数（本例中μ1=0.05，μ2=0.05），应用Matlab软件中的fsolve函数求解可以得到最优的频率比为η1=1.1777η2=0.9815。在满足最佳频率比的基础上，使三定点P、T、Q处取得极大值（或极大值附近），可以确定最优阻尼。运用软件Matlab编程实现，确定最优阻尼为ξ1=0.086、ξ2=0.102，参数优化结果，如图9所示。可以从图9看出，在系统的共振点附近有三个振幅峰值，而这三个峰值就是三个定点的位置，其他频率比的振幅均处于峰值以下，峰值基本持平且控制在4.5左右，系统在共振点附近的振幅比始终处于4.5以下，说明参数优化后可以有效控制系统共振点处的振幅。

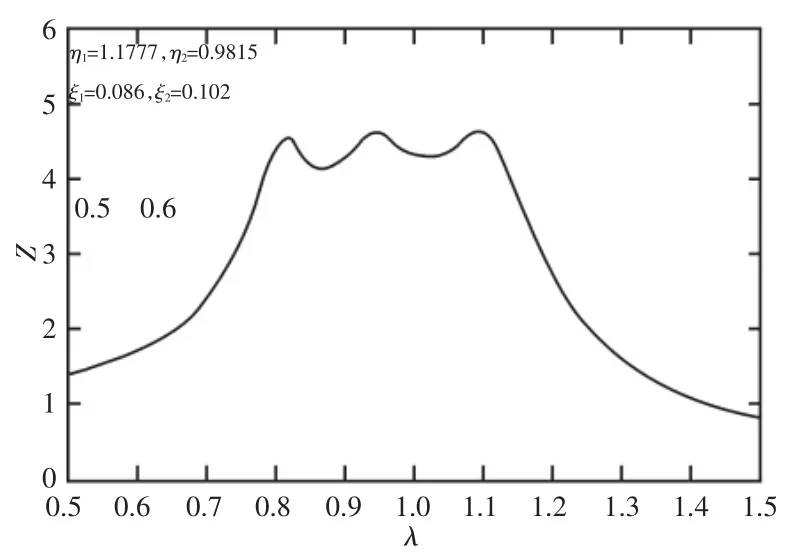
图9 参数优化后的系统振幅Fig.9 System Amplitude After Parameter Optimization

4 结论

提出了一种结构简单的二重滚珠式动力吸振器，通过解析和数值计算出了该结构的最优参数，通过凹槽内滚珠的运动来吸收部分主系统的振动能量，使吸振效果达到预期，有效降低强迫振动的响应。